Adapted from P. Coles, 1999, The Routledge Critical Dictionary of the New Cosmology, Routledge Inc., New York. Reprinted with the author's permission. To order this book click here: http://www.routledge-ny.com/books.cfm?isbn=0415923549
In particular many-particle systems,
phase transitions take place when processes occur that move the
system
between some disordered phase, characterised by a certain degree of
symmetry, and an ordered phase with a smaller degree of symmetry. In
this type of order-disorder transition, some macroscopic quantity
called the order parameter (here denoted by the symbol
) grows from
its original value of zero in the disordered phase. The simplest
physical examples of materials exhibiting these transitions are
ferromagnetic substances and crystalline matter. At temperatures above
a critical temperature TC (the Curie
temperature), the stable state of
a ferromagnet is disordered and has net magnetisation M = 0; the
quantity M in this case plays the role of the order parameter. At
temperatures below TC a nonzero magnetisation appears
in different
domains (called Weiss domains) and its direction in each domain breaks
the rotational symmetry possessed by the original disordered phase at
T > TC. In the crystalline phase of solids the
order parameter
represents the deviation of the spatial distribution of ions from the
homogeneous distribution they have at their critical temperature,
which is simply the freezing point of the crystal,
Tf. At temperatures
T < Tf the ions are arranged on a regular
lattice, which possesses a
different symmetry to the original liquid phase.
The lowering of the degree of symmetry of the system takes place even though the laws of physics that govern its evolution maintain the same degree of symmetry, even after the phase transition. For example, the macroscopic equations of the theory of ferromagnetism and the equations in solid-state physics do not favour any particular spatial position or direction. The ordered states that emerge from such phase transitions do, however, have a degree of symmetry which is less than that governing the system. We can say that the solutions corresponding to the ordered state form a degenerate set of solutions with the same symmetry as that possessed by the laws of physics. Returning to the above examples, the magnetisation M can in theory assume any direction. Likewise, the ions in the crystalline lattice can be positioned in an infinite number of different ways. Taking into account all these possibilities, we again obtain a homogeneous and isotropic state. Any small fluctuation, in the magnetic field of the domain for a ferromagnet or in the local electric field for a crystal, will have the effect of selecting one preferred solution from this degenerate set, and the system will end up in the state corresponding to that fluctuation. Repeating the phase transition with random fluctuations will eventually produce randomly aligned final states.
This is a little like the case of a free particle with velocity v and position r, described in Newtonian mechanics by the requirement that dv/dt = 0. This (very simple) law has both translational and rotational symmetries. The solutions of the equation are of the form r(t) = r0 + v0t, with some arbitrary initial choice of r = r0 and v = v0 at t = 0. These solutions form a set which respects the symmetry of the original equation. But the initial conditions r0 and v0 select, for one particular time, a solution from this set which does not have the same degree of symmetry as that of the equations of motion.
A symmetry-breaking transition, during which the order parameter
grows significantly, can be caused by external influences of
sufficient intensity. For example, a strong magnetic field can
magnetise a ferromagnet, even above the Curie temperature. Such
phenomena are called induced symmetry-breaking processes, in order to
distinguish them from spontaneous symmetry-breaking. The spontaneous
breaking of a symmetry comes from a gradual change of the parameters
of a system, such as its temperature.
It is useful to consider the free energy F of a system, which is
defined in thermodynamics to be F = E - TS,
where E is the internal
energy, T is the temperature and S is the entropy; the
condition for
the system to have a stable equilibrium state is that F must have a
minimum. The free energy coincides with the internal energy only at T
= 0. At higher temperatures, whatever the form of E, an increase in
the entropy (i.e. disorder) generally leads to a decrease in the free
energy F, and it is therefore favourable. for systems in which there
is a phase transition, F is a function of the order parameter
. Under
some circumstances the free energy F must have a minimum at
= 0
(corresponding to the disordered state), while in others it must have
a minimum for some
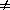0 (corresponding to the ordered state).
Let us now consider the simplest possible example. Suppose that the
situation we are dealing with respects a symmetry between
and -.
The free energy function F must also respect this symmetry, so that we
can expand F() in a power
series containing only even powers of :
where the coefficients
There are also first-order phase transitions, in which at
T = TC the
order parameter appears or disappears rapidly, and the difference
To apply these notions to cosmology we need also to take into
account quantum and thermal fluctuations and other effects of
non-equilibrium thermodynamics. Different symmetries in the past also
involved different fields interacting according to different
potentials. Nevertheless, the basic general properties of phase
transitions lie behind many models of the inflationary Universe.
FURTHER READING:
Kolb, E.W. and Turner, M.S., The Early Universe (Addison-Wesley,
Redwood City, CA, 1990).
) 
F0 + 
(T) 2 + 
(T) 4
and
of this expansion
depend explicitly on
temperature T. If > 0
and > 0, the curve
has one minimum at the
origin, so the equilibrium state lies at = 0. If the coefficients
change in such a way that at lower temperatures < 0 and > 0, the
original minimum becomes a maximum and two new minima appear at
= ± 
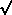( / 2);
in this case the disordered state is unstable, while the
minima correspond to degenerate ordered states with the same
probability. Any small external perturbation which renders one of the
two minima slightly deeper or nudges the system towards one of them
can make the system evolve towards one rather than the other. This is
how spontaneous symmetry-breaking occurs. If there is only one
parameter describing the system, say the temperature, and the
coefficient is written as
= a(T -
TC) with >
0, this transition
is called a second-order phase transition, and it proceeds by a
process known as spinodal decomposition: the order parameter appears
or disappears gradually, and the difference
F in free energy between
the two states is infinitesimally small when T is close to
TC.
F
between the old and new minima is finite. This difference is called
the latent heat of the phase transition. In first-order phase
transitions, when T decreases the phenomenon known as
supercooling can
occur: the system remains in the disordered state characterised by
=
0 even when T has fallen below the critical temperature. This is
because the original minimum represents a metastable equilibrium. A
local minimum of the free energy still persists there, protected by a
potential barrier that prevents the system from moving immediately
into the global minimum. As T decreases further, or the system is
perturbed by either internal or external fluctuations, the system
finally evolves into the global minimum that represents the true
energetically stable state. This liberates the latent heat that was
stored in the metastable state. The system, still in the ordered
state, is heated up again to a temperature of around
TC by the release
of this latent heat, a phenomenon called reheating.