


2.3. Luminosity and Mass Distributions
By far the most robust and predictable feature of the GCS in different
galaxies is the luminosity distribution of the clusters (LDF),
which is the visible trace of the cluster mass spectrum. In its
classic form plotted as number of clusters per unit magnitude
MV,
the LDF has a roughly Gaussian-like shape with a characteristic
``turnover'' or peak point at M
The potential use of the LDF for standard-candle purposes was, in fact,
the original stimulus for studying globular clusters in distant
galaxies, beginning with the Virgo ellipticals (see
Hanes 1977 and
H99).
But as more data have come in, and as the remarkable uniformity of the LDF
has emerged more clearly, it has become more interesting for its
strong astrophysical constraints on cluster formation and evolution.
The LDF in its entirety
must be the product of the initial mass spectrum of the
clusters at formation, combined with the
subsequent ~ 1010 years of
dynamical evolution in the tidal field of the parent galaxy.
Most of the relevant destruction mechanisms (tidal shocking due
to passage through the disk or bulge, evaporation coupled to the
tidal field) are much more effective at lower cluster mass, and
current models (e.g.
Murali & Weinberg 1997;
Gnedin & Ostriker 1997;
Vesperini 1997,
1998;
Vesperini & Heggie
1997;
and Elson's lectures in this volume) indicate that the
transition mass above which these effects are
not critically important is the LDF turnover near 105
M
Over the upper ~ 90% of the globular cluster mass range
(M
McLaughlin & Pudritz
(1996)
have developed a quantitative theory for the LDF
in which protocluster gas clouds build up within very large ``supergiant''
molecular clouds (SGMCs) by collisional agglomeration. The SGMC is
visualized as supplying a large number of initial
small-mass cloud ``particles'' (physically, these particles can
be visualized as probably resembling the ~ 100
M
The emergent mass spectrum from this collisional growth process has
the expected power-law form, but its detailed shape is controlled
by two key input parameters: (a) the ratio of cloud lifetime against
star formation relative to the cloud-cloud collision time; and
(b) the dependence of cloud lifetime on mass.
More massive clouds have higher mean densities and are
expected to have shorter lifetimes. Thus, cloud growth is a stochastic
race against time: large clouds continue to grow by
absorbing smaller ones, but as they do, their survival time before turning
into stars becomes shorter and shorter. Thus at the high-mass end,
the slope of the mass spectrum dN / dM gradually steepens as it becomes
more and more improbable that such massive clouds can survive before
turning into stars. Encouragingly, this very feature is
matched extremely well by the observations of LDFs in
populous cluster systems such as in giant ellipticals (see
McLaughlin & Pudritz
1996).
Even more encouraging is the fact that
this theory is also able to match the entire LDF of
the newly formed star clusters in recent mergers such
as NGC 4038 / 4039
(Whitmore & Schweizer
1995)
and NGC 7252
(Miller et al. 1997).
In these cases, we should be looking at something much closer to
the initial mass spectrum, relatively unaffected even at low masses by
dynamical evolution (see Figure 8).
Figure 8. Luminosity distribution function
(LDF, or number of
clusters per unit luminosity) for the ``young'' globular clusters
formed in the merger remnants NGC 4038 / 39 and NGC 7252.
The model lines
(from McLaughlin 1998,
private communication)
are computed from the collisional growth model of
McLaughlin & Pudritz
(1996).
The original gas ``particles'' have masses m0 = 100
M
The related new observations of globular clusters
in young and merging systems, some of which were used
above, represent a major stride
forward in our understanding of globular cluster formation.
Clusters are now seen to form in an amazingly wide
range of situations: in protogalactic halos, in starburst dwarf
galaxies with or without obvious external ``triggers'',
in merging disk galaxies, or at the centers of giant ellipticals
that are accreting gas. We see from the same observations that
cluster formation is a highly
inefficient process: the typical star cluster mass is ~ 10-3
of the host GMC mass, and any one GMC appears to produce
only a handful of star clusters that remain bound over many Gyr.
In other words, the star clusters end up using
typically less than 1% of the host GMC gas supply regardless
of environment (see
H99;
Kissler-Patig et
al. 1998;
McLaughlin 1999).
Although most
stars may well form in ``clustered'' mode, the majority of these
clumps and associations dissolve quickly away into the field, leaving
the bound clusters as those rare sites in which the star formation
efficiency was ~ 50% or more.
These observations show that it is no longer tenable
to regard globular cluster formation as a ``special'' event which
happened only in the early universe; though it is a rare mode of
star formation, it is also clearly a robust process which can happen
at any metallicity and at
any time that a sufficient supply of gas is collected together.
Exactly how the gas is accumulated into sufficiently
large SGMCs during the protogalactic era is of interest on its
own merit but is, apparently,
not a critical issue for the mass spectrum of the globular clusters
it produces.
At the present time, the collisional-growth model provides the only fully
quantitative theoretical fit to the cluster
mass spectrum at formation that we have available.
Though it is obviously successful as far as it goes, many steps
remain to be taken: for example, we would like to be able to
predict from the gas dynamics of the host GMCs what the cloud
lifetimes should be and exactly how the lifetime depends on mass.
We also need to understand why the ratio of cluster mass
to host GMC mass is typically ~ 10-3, and what fraction of
the total GMC mass can be expected to turn into clusters. (NB: In
Elmegreen & Efremov
(1997),
a somewhat different scenario is
adopted in which the mass distribution of clouds within a GMC is
stated to resemble a fractal structure generated by turbulence.
In this scheme, however,
the expected slope dN / dM ~ M-2 is slightly
too steep to match most real galaxies, and does not clearly predict
the progressive change in slope with mass
that is embedded in the collisional growth model.)
 -7.4, differing by little
more than ± 0.2 magnitudes from any one large galaxy to another.
The symmetric Gaussian-like shape has been consistently verified
in every galaxy with sufficiently deep photometry (e.g.,
Harris et al. 1991;
Whitmore et al. 1995;
Kundu & Whitmore 1998),
and the turnover luminosity is consistent enough to be an
entirely respectable standard candle for distance determination (see
H99;
Whitmore 1997;
Harris 1997
for comprehensive recent discussions).
-7.4, differing by little
more than ± 0.2 magnitudes from any one large galaxy to another.
The symmetric Gaussian-like shape has been consistently verified
in every galaxy with sufficiently deep photometry (e.g.,
Harris et al. 1991;
Whitmore et al. 1995;
Kundu & Whitmore 1998),
and the turnover luminosity is consistent enough to be an
entirely respectable standard candle for distance determination (see
H99;
Whitmore 1997;
Harris 1997
for comprehensive recent discussions).
 .
Above this point, the LDF we observed today is therefore likely to
be much closer to the original mass spectrum at the time of formation.
Although a consensus is gradually growing in this direction,
more comprehensive dynamical simulations incorporating the full range
of dynamical effects, starting from a realistic
formation mass spectrum, still need to be done.
.
Above this point, the LDF we observed today is therefore likely to
be much closer to the original mass spectrum at the time of formation.
Although a consensus is gradually growing in this direction,
more comprehensive dynamical simulations incorporating the full range
of dynamical effects, starting from a realistic
formation mass spectrum, still need to be done.
 105
M
105
M , where the
very most massive clusters reach
as high as ~ 107
M
, where the
very most massive clusters reach
as high as ~ 107
M ), the cluster
mass spectrum is better
plotted as number of clusters per unit mass or unit luminosity,
rather than per unit magnitude. In this form, it
is well described by a simple power-law form
dN / dM ~ M-1.8 ± 0.2 in all galaxies
(Harris & Pudritz
1994),
gradually steepening to higher masses.
This distribution is the form which needs to be reproduced by
a quantitative formation model; it also needs to be virtually independent
of other factors such as metallicity, total cluster population
(SN), or size and type of host galaxy!
Whatever mechanism we settle on must be extremely robust.
), the cluster
mass spectrum is better
plotted as number of clusters per unit mass or unit luminosity,
rather than per unit magnitude. In this form, it
is well described by a simple power-law form
dN / dM ~ M-1.8 ± 0.2 in all galaxies
(Harris & Pudritz
1994),
gradually steepening to higher masses.
This distribution is the form which needs to be reproduced by
a quantitative formation model; it also needs to be virtually independent
of other factors such as metallicity, total cluster population
(SN), or size and type of host galaxy!
Whatever mechanism we settle on must be extremely robust.
 cloud
cores found in Galactic GMCs). These cloud particles then collide
and amalgamate to form larger ones; after several crossing times,
a power-law distribution of cloud masses results (e.g.,
Field & Saslaw 1965;
Kwan 1979).
The larger clouds become
the ``protoclusters'' which eventually turn into full-fledged
star clusters once their internal pressure support (due to turbulence
and weak magnetic field) leaks away. Since the small clouds always
vastly outnumber the large ones, the reservoir of gas contained
in the entire SGMC needs to be very much larger than the masses of the
individual protoclusters that build up inside it
(observationally, the typical star cluster
mass is ~ 10-3 of the host GMC mass; see
Harris & Pudritz 1994).
cloud
cores found in Galactic GMCs). These cloud particles then collide
and amalgamate to form larger ones; after several crossing times,
a power-law distribution of cloud masses results (e.g.,
Field & Saslaw 1965;
Kwan 1979).
The larger clouds become
the ``protoclusters'' which eventually turn into full-fledged
star clusters once their internal pressure support (due to turbulence
and weak magnetic field) leaks away. Since the small clouds always
vastly outnumber the large ones, the reservoir of gas contained
in the entire SGMC needs to be very much larger than the masses of the
individual protoclusters that build up inside it
(observationally, the typical star cluster
mass is ~ 10-3 of the host GMC mass; see
Harris & Pudritz 1994).
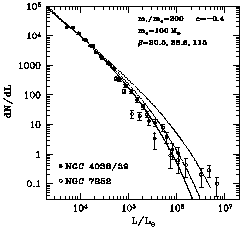
 , the cloud
lifetime varies as
, the cloud
lifetime varies as
 ~ m-0.4, and
the parameter
~ m-0.4, and
the parameter  defines the ratio of fiducial cloud lifetime to
collisional crossing time. Larger values of
defines the ratio of fiducial cloud lifetime to
collisional crossing time. Larger values of
 generate shallower
mass functions that extend to higher mass.
In this case a relatively small value
generate shallower
mass functions that extend to higher mass.
In this case a relatively small value

 20 fits the data.
20 fits the data.