


5.1. The Role of the Halo Gas: Understanding High SN
New clues emerging from the recent surveys
(Blakeslee 1997;
Blakeslee et al. 1997;
Harris et al. 1998)
show rather clearly that SN for these large galaxies displays
a continuum of values from the ``normal''
SN0  3-4
up to 15 and more. More importantly, SN is clearly
correlated with the luminosity of the BCG,
and with the total mass of the surrounding galaxy cluster as measured
by the velocity dispersion of the galaxies or the temperature and
luminosity of the hot X-ray gas in the cluster potential.
Larger BCGs are found in more massive potential wells, and have higher
specific frequencies.
3-4
up to 15 and more. More importantly, SN is clearly
correlated with the luminosity of the BCG,
and with the total mass of the surrounding galaxy cluster as measured
by the velocity dispersion of the galaxies or the temperature and
luminosity of the hot X-ray gas in the cluster potential.
Larger BCGs are found in more massive potential wells, and have higher
specific frequencies.
Let us go back to the definition of SN. To obtain an unusually high ratio Ncl / Lgal, we really have only two ways to do it. (a) First, we can increase Ncl at a given Lgal. This route remains arbitrary, since we have no physical theory for predicting the formation efficiency e. (b) Second, we can decrease Lgal for the same number of clusters. The most obvious way to take this second path, following the clues mentioned above for NGC 5128 and NGC 4472, is to leave a lot of the original gas supply unused. To put this another way, we can assume that Ncl is proportional to the original protogalactic gas mass; but that in certain galaxies (the BCGs in particular), for whatever reason a large amount of the gas ended up not being converted to stars.
This latter option is raised by Blakeslee (1997) and Harris et al. (1998) and pursued extensively by McLaughlin (1999). Summarizing their arguments, suppose now that we redefine the globular cluster formation efficiency as a mass ratio,
where M* is the mass now in visible stars, while
Mgas is the remaining mass in the galactic halo which was
originally part of the protogalaxy. We now explicitly assume
that
McLaughlin (1999)
tests this idea quantitatively by showing
that in three well studied galaxies (M87 and NGC 4472 in
Virgo
and NGC 1399 in Fornax), the ratio of mass densities
There are two principal effects acting to define the shape of
this relation: first is that
the mass-to-light ratio increases gradually with luminosity
(M/L ~ L0.3), so that bigger ellipticals have
more clusters
per unit light. Second is that bigger BCGs have much more surrounding
halo gas, thus (by hypothesis)
they generated many more clusters at early times. Combining
both of these effects, McLaughlin shows that the overall
relation between Ncl and Lgal
matches the BCG pattern
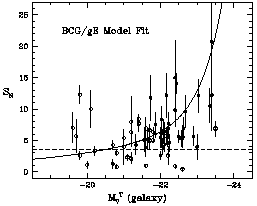
remarkably well (Figure 12). In the graph, the
solid line
representing the
Figure 12. Relation between specific
frequency and galaxy luminosity
for giant E galaxies (BCGs are shown by filled circles, other giant
ellipticals by open circles. The dashed line indicates
SN = 3.5 shown previously in
Figure 7. The solid line is from
the model of
McLaughlin (1999),
in which a constant globular cluster
formation efficiency
This model provides, for the first time, a plausible and
quantitative view of the specific frequencies in BCGs,
and as such, gives us a partial solution to the overall
problem of understanding the global galaxy-to-galaxy scatter
in specific frequency. Clearly, interesting anomalies still remain
above and below the mean line. Do all the E galaxies with
very lowSN values represent merger remnants? And do the
few remaining normal ellipticals
with anomalously high SN represent cases
of genuinely more efficient cluster formation?
In addition, for the BCGs themselves, it is still not certain
how the large amounts of halo gas were left in place:
the gas might have been ejected and heated during the earliest star
formation phase by the first round of supernovae, as we speculated
earlier for NGC 5128 (this phase would have had to be particularly
violent and short-lived to distinguish it from other, more normal
ellipticals, perhaps involving a major galactic wind; see
Harris et al. 1998).
Alternately, the protogalactic SGMCs
may have been stripped of much of their
gas in the deep central BCG potential well before star formation could
begin in earnest
(Blakeslee 1997).
Whatever the answer, these
large central galaxies represent an extreme set of conditions
which still needs to be modelled in detail.
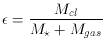
 is constant,
and thus the total number
of globular clusters is directly proportional to the
original protogalactic mass. (We do not expect, of course,
that
is constant,
and thus the total number
of globular clusters is directly proportional to the
original protogalactic mass. (We do not expect, of course,
that  can be precisely the
same in all environments,
since cluster formation must at some level be a stochastic process.
We are, however, using this hypothesis to reduce the
order-of-magnitude differences in SN down to much smaller
levels that can more easily be accommodated within the observational
scatter.) In most galaxies, Mgas is much smaller than
M*:
their halos do not contain much leftover gas. However, the
BCGs usually have quite large amounts of high-temperature X-ray gas,
and the amount goes up dramatically with luminosity
(MX ~ Lgal2.5). For the
very biggest BCGs,
Mgas is larger than M*, which would
require us to assume
in this picture that most of their protogalactic gas is
still unconverted.
can be precisely the
same in all environments,
since cluster formation must at some level be a stochastic process.
We are, however, using this hypothesis to reduce the
order-of-magnitude differences in SN down to much smaller
levels that can more easily be accommodated within the observational
scatter.) In most galaxies, Mgas is much smaller than
M*:
their halos do not contain much leftover gas. However, the
BCGs usually have quite large amounts of high-temperature X-ray gas,
and the amount goes up dramatically with luminosity
(MX ~ Lgal2.5). For the
very biggest BCGs,
Mgas is larger than M*, which would
require us to assume
in this picture that most of their protogalactic gas is
still unconverted.
 cl /
(
cl /
( * +
* +
 gas)
throughout the
halo is equal to
gas)
throughout the
halo is equal to  0.0025
in all three galaxies. That is, the addition of the X-ray gas mass
makes this ratio much more nearly consistent with the hypothesis
that there is a quasi-universal cluster
formation efficiency
0.0025
in all three galaxies. That is, the addition of the X-ray gas mass
makes this ratio much more nearly consistent with the hypothesis
that there is a quasi-universal cluster
formation efficiency  .
By using the fundamental plane relations for E galaxies which
relate the mass-to-light ratio, scale radius, and internal velocity
dispersion to Lgal, McLaughlin (1999) also shows that
the ratio Mgas / M* scales as
Lgal1.5,
leading to the following scaling for the specific frequency:
.
By using the fundamental plane relations for E galaxies which
relate the mass-to-light ratio, scale radius, and internal velocity
dispersion to Lgal, McLaughlin (1999) also shows that
the ratio Mgas / M* scales as
Lgal1.5,
leading to the following scaling for the specific frequency:
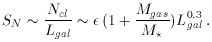
 =
constant = 0.0025 model continues
to steepen at higher luminosity because of the progressively
increasing relative amounts of halo gas.
=
constant = 0.0025 model continues
to steepen at higher luminosity because of the progressively
increasing relative amounts of halo gas.
 per
unit initial gas mass is
assumed. The curve ramps up steeply at high luminosity to account
for the observation that more luminous BCGs have considerably more
high-temperature halo gas (see text).
per
unit initial gas mass is
assumed. The curve ramps up steeply at high luminosity to account
for the observation that more luminous BCGs have considerably more
high-temperature halo gas (see text).