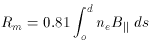Discovered in 1967, pulsars are the rapidly rotating core left behind by exploding Type II supernovae. More than a thousand have now been observed in our Galaxy, in halo globular clusters, and in the LMC and SMC. Radio observations of these rapidly pulsating stars provide information on the plasma densities and magnetic field strengths of the intervening interstellar medium over base lines of tens of kiloparsecs.
The electrodynamic properties of a plasma are functions of the frequency of the electromagnetic wave that traverses the plasma. The group velocity of a wave in a plasma is
where
Because the group velocity of a wave depends on its frequency, the fourier
components of a pulse will traverse a total distance d through a plasma
in a time t
where s defines a small increment of distance through the plasma.
Plasma frequencies in interstellar space are typically very low so
we can expand eqn. 3 and substitute into eqn. 5 such that the time taken for
the fourier component of a pulse to traverse a plasma is
The first term is the time taken to traverse a distance d in vacuo, and
the second term is the plasma correction.
Studies of the arrival times of the various fourier components indicate that
the highest frequencies arrive ahead of the low frequency components. What
is actually measured is the derivative of eqn. 5,
The dispersion measure, defined as Dm =
Figure 5. Dispersion measures from pulsars,
Dm sin b where b is galactic
latitude, versus z-distance above the Galactic plane. The horizontal
lines show the distance uncertainty for different pulsars. The black
circles and stars refer to pulsars in globular clusters and the Magellanic
clouds respectively. The sloping line corresponds to a model electron
distribution which is uniform in density 0.03 cm-3, and the two
dashed lines are for models in which the electron layer has the same
density at z = 0 but falls off with increasing z as
sech2(z/h)
where h is 500 pc and 800 pc.
(Courtesy of R.N. Manchester, Australia Telescope National Facility.
The radio signals reveal other important properties about the diffuse
gas. In the presence of a magnetic field along the path to the pulsar,
B||, the plane of polarization of the propagating wave
will rotate
by an angle
for which
in the traditional units of rad m-2, and
where B|| is in units of microgauss
(µG). The ratio of Rm to
Dm is the average galactic magnetic field strength
along the path,
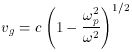
is the angular frequency and
p is the plasma
frequency defined by
2p
= 4
n e2 / m,
for which n, e and m are the number density, charge
and mass of the free electrons.
given by
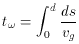
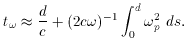
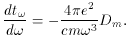
0d ne ds,
is a measure of the total column of free electrons along the path to
the pulsar in units of pc cm-3. A column of 1020
electrons results
in a Dm of 30 pc cm-3 and a delay of 12 sec
for a signal at 100 MHz
relative to infinite frequency. Dispersion measures were first obtained by
the pulsar discovery team. Since then, we have come to learn
(Fig. 5)
from pulsars in distant globular clusters and
the Magellanic Clouds that the warm atmosphere in the Galaxy
extends to about a kiloparsec above the Galactic plane.
equal to the phase
delay between the ordinary and
extraordinary components of the electric field. The so-called Faraday
rotation angle is given by
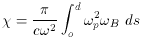
B is the
cyclotron frequency. We define a quantity called the rotation measure,
