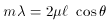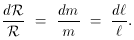The ideal filter is an imaging device which can isolate
an arbitrary spectral band
at an arbitrary wavelength
over a broad, continuous
spectral range, preferably with
a response function which is identical in form at all wavelengths.
The tilting interference filter is much the worst form of tunable filter. The spectral range covered is almost negligible, and the filter profile varies with tilt angle. Some devices (e.g., Lyot, linear variable filter) work only at a fixed resolving power but have the ability to tune over a wide spectral window. Better devices allow for a wide selection of resolving powers over a wide range of wavelengths.
The different techniques rely ultimately on the interference of beams that traverse different optical paths to form a signal. The technologies which come closest to the ideal tunable filter are the air-gap Fabry-Perot and Michelson (Fourier Transform) interferometers. To understand why, we highlight the Taurus Tunable Filter (TTF) which was the first general purpose device for night-time astronomy (see http://www.aao.gov.au/local/www/jbh/ttf). This is a Fabry-Perot filter where interference is formed between two highly reflective, moving plates. To be a useful filter, not only must the plates move through a large physical range, but they must start at separations of only a few wavelengths, as we show.
|
Figure 1. (i) Interference filter: the internal structure is not shown. (ii) Fabry-Perot etalon. (iii) Wedged Fabry-Perot etalon which avoids the problem of the plates behaving like interference filters. |
The condition for photons with wavelength
to pass through
the filter is (see Fig. 1)
from which it follows that
For an order of interference m, the resolving power is
R = m N where N is the instrumental finesse.
The finesse is determined by the coating reflectivity and is
essentially the number of recombining beams. For the TTF,
the plates can be scanned over the range l = 1.5-15
µm, and the
orders of interference span the range m = 4-40, such that the
available resolving powers are R = 100-1000.
The sharp core of almost all tunable-filter transmission profiles is
not ideal. Even a small amount of flatness at peak
transmission can ensure that we avoid narrowly missing most of the
spectral line signal from a source. In theory, all band-limited functions
can be squared off, but in practice this is difficult for all but two
devices. Since the Michelson interferometer (filter) obtains its data in the
frequency domain, the profile can be partially squared off at the data
reduction stage through a suitable choice of convolving function. For the
Solc filter, the instrumental profile can be modified through the
use of partial polarizers and birefringent retarder elements.
