Copyright © 1991 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1991. 29:
89-127 Copyright © 1991 by Annual Reviews. All rights reserved |
2.5 Stars
Several point sources (stars) appear in Figure 4 and then disappear as the spatial scan proceeds. These spectra are evident in the figure as horizontal bands of emission, strongest at the longest wavelengths and fading out at the shortest wavelengths.
These stars are, of course, a nuisance as they are noise in the background that is sought. But they can be much worse than a nuisance, for if one's spectrometer or photometer has no imaging capability, as is the case in the majority of past experiments, radiation from a star that is in the field of view but that is not known to be in the field will be misinterpreted as diffuse ultraviolet background radiation. And since there are many more faint stars at low Galactic latitudes, the false background that is inferred will correlate nicely with Galactic latitude. This problem is discussed specifically as we describe the various experiments in what follows. Here, we simply give a general characterization of the spatial and spectral character of the stellar ultraviolet sky.
|
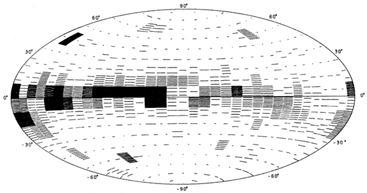
Figure 7. Predicted brightness of the sky at 1482 Å, from stars only (30). The map is drawn with Gould coordinates. Note the strong concentration of starlight to one half of the Gould plane. |
The appearance of that sky as predicted in a previous study (30) is shown in Figure 7, which is a map of the sky at 1482 Å, in Gould coordinates. Gould coordinates are galactic coordinates tipped by about 19°. Figure 7 shows that they are the physically meaningful system for this problem - the stars that are contributing most of the ultraviolet light are located in the Gould belt, not in the galactic plane. Observational confirmation that the sky has the predicted appearance came from a rocket flight (39), from which the data shown in Figure 8 were obtained. Figure 8 is oversaturated, unlike Figure 7. This has been done to bring out fainter surface brightnesses more clearly. Additional confirmation of the Figure 7 prediction was obtained by Gondhalekar, Phillips & Wilson (27) who mapped all of the stars observed with the S2/68 experiment (6) on the TD-1 satellite. The difference between their observational map and the much cruder observational map of Figure 8 - and what makes Figure 8 of extra interest - is that their map includes only the direct light of stars. In contrast, the data used to form Figure 8 were obtained with a sensitive detector having a full width at half-maximum transmission of fully 10°. This means that, in addition to the direct light of stars, Figure 8 maps diffuse radiation plus the integrated light of even the faintest stars. This means in turn that the faintness of the Galactic plane in regions where the Gould belt departs significantly from that plane in Figure 7 might be accounted for by incompleteness of the star catalogue from which the map was made, but the same faintness in Figure 8 is surely due to interstellar extinction. We have determined in this way that the far-ultraviolet interstellar radiation field is totally dominated by relatively nearby stars; hardly unexpected, but nice to have demonstrated.
|
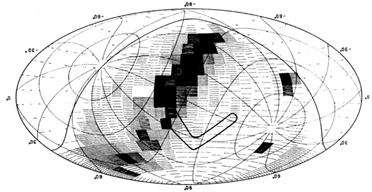
Figure 8. Observation of the sky at 1500 Å (39). The observed distribution agrees generally with the prediction of Figure 7. This map is drawn in Celestial coordinates, and a grid of Galactic coordinates is superposed. Grey scale intensity at highest latitude is 1600 units, perhaps due to residual airglow. |
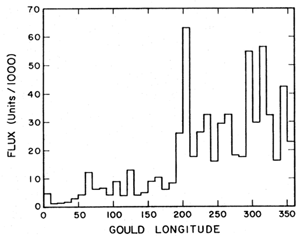
One feature of Figure 7 to be noted (and that is confirmed observationally in Figure 8) is the exceedingly strong anistropy of the local far-ultraviolet interstellar radiation field, with regard to Gould (and therefore Galactic) longitude. This anistropy has been evaluated quantitatively using the TD-1 data, in a painstaking study by Landsman (60). Landsman's result is shown in Figure 9, where the average surface brightness over a band of width ± 20° centered on the Gould equator is plotted as a function of longitude. The flux over half the plane is as low as ~ 5000 units, and for one region of longitude it is only ~ 1000 units! This is important in what follows.
|
Figure 9. The anisotropy in Gould longitude that appears in Figures 7 and 8 as given by Landsman (60) who used TD-1 data. |
Another important feature of Figure 7 is the extreme concentration of the starlight to one half of the Gould plane. The star-catalogue integration has been plotted (30) as a function of Gould latitude. One important point in examining that plot is the comparison with the models of van de Hulst and de Jong (113), which were computed from visible light data.
A final remark on the problem of stars: looking back at our template again, Figure 4, we see that the effect of stars tends to disappear at the shortest wavelengths. This is not an instrumental effect: while Figure 4 has not been corrected for instrumental sensitivity, the sensitivity at, say, 1400 Å is comparable to that at 2500 Å. The explanation is that stars hot enough to contribute significantly at the shorter wavelengths are rare at moderate and high latitudes. Mentioned above (and discussed in greater detail below) is the severe danger that undetected stars pose for photometric study of the diffuse background. Figure 4 clearly shows that the danger is smallest for the shortest wavelength experiments. Above all, the danger is minimal for those experiments that have been sensitive to radiation below 1216 Å; namely shortward of the entire range of Figure 4.