


3.1 Fitting the Spectra of Accretion Disks
As material falls toward a black hole, it is believed to settle into an accretion disk in which angular momentum is dissipated by viscosity. From the virial theorem, half of the gravitational potential energy U is radiated. Therefore the luminosity is
At sufficiently high accretion rates
Here 2
Parameterizing the above result in terms of the Eddington accretion rate,
In other words, the peak of the blackbody spectrum occurs at a frequency of
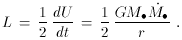
 BH, the gas is optically
thick, and the disk radiates as a thermal blackbody:
BH, the gas is optically
thick, and the disk radiates as a thermal blackbody:
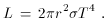
 r2 is the
surface area of the disk and
r2 is the
surface area of the disk and  is the
Stefan-Boltzmann constant. The effective temperature of the disk as a function
of radius r is therefore
is the
Stefan-Boltzmann constant. The effective temperature of the disk as a function
of radius r is therefore
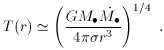
 E
E
 LE /
LE /
 c2 = 2.2
(
c2 = 2.2
( / 0.1)-1
(MBH/108
/ 0.1)-1
(MBH/108
 )
)
 yr-1, and the
Schwarzschild radius,
RS
yr-1, and the
Schwarzschild radius,
RS  2GMBH /
c2 = 2.95 x 1013
(MBH/108
2GMBH /
c2 = 2.95 x 1013
(MBH/108
 ) cm, gives
) cm, gives
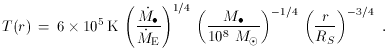
 max = 2.8 kT/h
max = 2.8 kT/h
 4 x 1016 Hz, where
k is Boltzmann's
constant and h is Planck's constant. This peak is near 100 Å
or 0.1 keV.
In fact, the spectra of many AGNs show a broad emission excess at extreme
ultraviolet or soft X-ray wavelengths. This ``big blue bump'' has often been
identified with the thermal emission from the accretion disk. A fit to the
luminosity and the central frequency of the big blue bump gives
MBH and
4 x 1016 Hz, where
k is Boltzmann's
constant and h is Planck's constant. This peak is near 100 Å
or 0.1 keV.
In fact, the spectra of many AGNs show a broad emission excess at extreme
ultraviolet or soft X-ray wavelengths. This ``big blue bump'' has often been
identified with the thermal emission from the accretion disk. A fit to the
luminosity and the central frequency of the big blue bump gives
MBH and
 BH but not each
separately. Corrections for disk inclination and
relativistic effects further complicate the analysis. This method is therefore
model-dependent and provides only approximate masses. Typical values for
quasars
are MBH
BH but not each
separately. Corrections for disk inclination and
relativistic effects further complicate the analysis. This method is therefore
model-dependent and provides only approximate masses. Typical values for
quasars
are MBH  108 - 109.5
108 - 109.5
 and
and
 BH
BH
 0.1 - 1
0.1 - 1
 E. Seyfert nuclei
appear to have lower
masses, MBH
E. Seyfert nuclei
appear to have lower
masses, MBH  107.5 - 108.5
107.5 - 108.5
 , and lower
accretion rates,
, and lower
accretion rates,  BH
BH
 0.01 - 0.5
0.01 - 0.5
 E.
E.