


3.1. The Standard Model and Everyday Life
The Standard Model of fundamental quantum fields has at least 20 adjustable parameters (including for this count Einstein's classical theory of gravity), although it explains almost all natural phenomena with less than half of these, and the basic structures are fixed by just a handful of them. At a deeper level, the values of the parameters are presumed to be not all truly independent and adjustable; symmetries fix relationships between some of them.
The minimal Standard Model has 19 ``adjustable'' parameters
(Cahn 1996,
Gaillard et al. 1999):
Yukawa coefficients fixing the masses of the six quark
and three lepton flavors (u, d, c, s, t, b, e, µ,
 ), the Higgs mass
and vacuum expectation value v (which multiplies the
Yukawa coefficients to determine the fermion masses), three angles and one
phase of the CKM (Cabibbo-Kobayashi-Maskawa) matrix (which mixes quark
weak- and
strong-interaction eigenstates), a phase for the quantum chromodynamic
(QCD) vacuum,
and three coupling constants g1, g2,
g3 of the
gauge group, U(1) x SU(2) x SU(3).
If as seems likely the neutrinos are not massless, there
are seven more parameters for them
(three masses and another four CKM matrix elements).
), the Higgs mass
and vacuum expectation value v (which multiplies the
Yukawa coefficients to determine the fermion masses), three angles and one
phase of the CKM (Cabibbo-Kobayashi-Maskawa) matrix (which mixes quark
weak- and
strong-interaction eigenstates), a phase for the quantum chromodynamic
(QCD) vacuum,
and three coupling constants g1, g2,
g3 of the
gauge group, U(1) x SU(2) x SU(3).
If as seems likely the neutrinos are not massless, there
are seven more parameters for them
(three masses and another four CKM matrix elements).
Various more or less observable combinations of these parameters
appear in discussing phenomenology, taking account of
the change of couplings with energy.
The traditional zero-energy electromagnetic fine structure constant
 = e2 = 1/137.03599,
changes with energy scale to
= e2 = 1/137.03599,
changes with energy scale to
 (mZ)
(mZ)
 1/128
at the Z mass scale; it is related to the electroweak parameters by
e = g2
sin
1/128
at the Z mass scale; it is related to the electroweak parameters by
e = g2
sin  W, where
the weak mixing angle
tan
W, where
the weak mixing angle
tan  W
W
 g' / g2
also fixes the W and Z mass ratio, sin2
g' / g2
also fixes the W and Z mass ratio, sin2
 W = 1 -
(mW2 / mZ2),
and for consistently normalized currents one defines
g1 = sqrt(5/3)g'.
The Fermi constant of weak
interactions can be written
W = 1 -
(mW2 / mZ2),
and for consistently normalized currents one defines
g1 = sqrt(5/3)g'.
The Fermi constant of weak
interactions can be written
where v = 246 GeV is the expectation value of the Higgs
field. The strong
coupling
The Standard
Model plus classical gravity describes all known physical
phenomenology within the
present-day universe. Everyday matter (indeed nearly all
of the ``baryonic'' matter of the universe aside from energetic particles)
is almost entirely made of the lightest first generation
fermions. (4)
Since we may take the strong coupling to be fixed at
the proton mass scale, and the fermion masses enter mostly through their
ratio to the nucleon mass, the basic structures (almost) just depend on
four parameters, which we may take to be
the three light fermion masses me,
mu, md and the elecromagnetic
coupling constant
The electron mass and fine structure constant together determine
the basic behavior of atomic matter and its interaction
with radiation - in other words, all of chemistry and biology.
They enter in familiar combinations
such as the classical electron radius re =
The detailed relationships among atomic and molecular eigenstates are
not preserved continuously or homologously as
This amazing achievement of quantum theory illuminates another good example
of failed anthropic reasoning. Before quantum mechanics, it was
suggested that atomic properties must have been tuned
to achieve the marvellous chemical structures
needed for life
(Henderson 1913).
Instead it appears that ordinary Darwinian natural selection has
found and exploited the structural opportunities
presented by underlying symmetries. Biology and
not physics or cosmology should be given credit for this miracle!
By contrast,
changing the quark masses even a small amount has drastic
consequences which no amount of Darwinian selection can
compensate.
The u-d mass difference in particular attracts attention because the
d is just enough heavier than u to overcome the
electromagnetic energy difference to make the proton (uud) lighter
than the neutron
(udd) and therefore stable. On the other hand if it were a little
heavier still, the deuteron would be unstable and it would
be difficult to assemble any nuclei heavier than hydrogen.
This then is a good candidate for selective tuning among
multiverses. Similarly,
the sum of the quark masses controls the pion mass,
so changing them alters the
range of the nuclear potential and significantly changes nuclear structure
and energy levels. Even a small change radically alters the
history of nuclear astrophysics, for example,
by eliminating critical resonances of nucleosynthesis
needed to produce abundant carbon
(Hoyle et al. 1953).
It would be surprising if symmetries conspired to
satisfy these constraints, but quite natural if
the parameters can adopt a continuous range of values.
One therefore expects these particular parameters to
continue to elude relationships fixed by symmetries.
3 The relation of
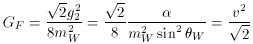
 S
S
 g32 can be defined
at some energy scale
g32 can be defined
at some energy scale  , say
, say
 s(
s( = mZ)
= 0.12; or, an
energy scale
= mZ)
= 0.12; or, an
energy scale  QCD
QCD
 200 MeV
can be defined where the coupling diverges. The masses of protons
and other hadrons are thereby approximately fixed by the value of
200 MeV
can be defined where the coupling diverges. The masses of protons
and other hadrons are thereby approximately fixed by the value of
 S at any
energy. (3)
S at any
energy. (3)
 , plus gravity.
(5)
Newton's constant of universal gravitation G specifies the
coupling of all forms of energy to gravity (which is usually regarded as
outside the ``Standard Model'').
In the next section we review how the gravitational coupling of nucleons
Gmproton2 defines the relationship between
the structure of the
astronomical scales of the universe and those of the microworld.
, plus gravity.
(5)
Newton's constant of universal gravitation G specifies the
coupling of all forms of energy to gravity (which is usually regarded as
outside the ``Standard Model'').
In the next section we review how the gravitational coupling of nucleons
Gmproton2 defines the relationship between
the structure of the
astronomical scales of the universe and those of the microworld.
 /me,
the Thomson cross section
/me,
the Thomson cross section
 T =
(8
T =
(8 /3)(
/3)( / me)2,
the electron Compton wavelength
/ me)2,
the electron Compton wavelength
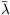 e =
me-1, and
the Bohr radius aBohr =
(
e =
me-1, and
the Bohr radius aBohr =
( me)-1.
The Rydberg energy
me
me)-1.
The Rydberg energy
me 2 / 2 sets the scale of atomic binding; atomic
fine structure (spin-orbit)
splittings depends on higher powers of
2 / 2 sets the scale of atomic binding; atomic
fine structure (spin-orbit)
splittings depends on higher powers of
 , and splittings of
molecular modes, which include electronic,
vibrational and rotational states, depend on powers of
me / mproton.
, and splittings of
molecular modes, which include electronic,
vibrational and rotational states, depend on powers of
me / mproton.
 and me are
adjusted, and would be scrambled with even small changes.
However, structural chemistry would not change much
if
and me are
adjusted, and would be scrambled with even small changes.
However, structural chemistry would not change much
if  and me
were adjusted slightly differently.
The structure of electron orbitals in atoms and molecules scales
homologously in first order with the Bohr radius, and the energy
levels of the ground-state orbitals scale with the Rydberg. So,
while it does seem miraculous that complementary structures
can form with the specificity (say) of purines and pyramidines in DNA,
the possibility of this
miracle can be traced back to group theory and quantum mechnanics;
if
and me
were adjusted slightly differently.
The structure of electron orbitals in atoms and molecules scales
homologously in first order with the Bohr radius, and the energy
levels of the ground-state orbitals scale with the Rydberg. So,
while it does seem miraculous that complementary structures
can form with the specificity (say) of purines and pyramidines in DNA,
the possibility of this
miracle can be traced back to group theory and quantum mechnanics;
if  and/or me
changed, the DNA structure would remain almost the same,
it would just change size relative to, say, the classical electron radius.
(The departure from homology enters only in subdominant
terms in the Hamiltonian, such as the spin-orbit or
nucleus-nucleus interactions.)
and/or me
changed, the DNA structure would remain almost the same,
it would just change size relative to, say, the classical electron radius.
(The departure from homology enters only in subdominant
terms in the Hamiltonian, such as the spin-orbit or
nucleus-nucleus interactions.)
 QCD to
QCD to
 S(E)
also depends on the fermion and Higgs masses, through threshold effects.
Back.
S(E)
also depends on the fermion and Higgs masses, through threshold effects.
Back.
4 The higher generations are less
prominent in nature than the first because they are
heavier and decay by weak interactions, although they are always
present at some level because of mixing and probably play important roles in
supernova physics and other exotic but important astrophysical environments
such as neutron stars. They also enter through the CKM matrix,
one complex phase of which is a source of observed CP violation
and therefore possibly
related to the physics responsible for creating the cosmic
excess of matter over antimatter. The masses of the heavy
fermions matter little to familiar natural phenomenology, so they could
be set by the choices selectively adopted by the
first generation if the fermion masses of the three generations
are (as is conjectured) coupled to each other in a unified scheme by a
mixing matrix. There are many such schemes proposed
(Berezhiani 1996);
for example, in the ``democratic'' scenario of
Fukugita, Tanimoto
and Yanagida (1999),
the nine fermion masses
are determined by five parameters, and still only two independent parameters
determine the masses of u, d, e (with md /
me fixed by SO(10)).
Back.
5
Agrawal et al. (1998)
have developed
the point of view
that the weak scale itself is determined anthropically and that v is
the one tunable
parameter - singled out in the standard model by having a dimension.
Indeed the fundamental degrees of freedom of the fundamental
theory are not known and one of the main objectives of studies such
as these is to sniff them out. Here I imagine adjusting some
coefficients in the Lagrangian according to the constraints imposed
by unification. This amounts to exploring a different space of
variation, with more degrees of freedom, than Agrawal et al.
For most of the arguments presented here, it does not matter whether
the Higgs is counted as a separate degree of freedom.
Note however that tuning only the Higgs varies all the fermion masses
in lockstep, and cannot by itself tune more than one degree of freedom.
Back.