The Hubble constant H0 is the constant of proportionality between recession speed v and distance d in the expanding Universe;
The subscripted ``0'' refers to the present epoch because in general
H changes with time. The dimensions of H0 are
inverse time, but it is usually written
where h is a dimensionless number parameterizing our ignorance. The
inverse of the Hubble constant is the Hubble time tH
and the speed of light c times the Hubble time is the Hubble
distance DH
These quantities set the scale of the Universe, and often cosmologists
work in geometric units with c = tH =
DH = 1.
The mass density
(Peebles 1993,
pp. 310-313), where the subscripted ``0''s indicate
that the quantities (which in general evolve with time) are to be
evaluated at the present epoch. A third density parameter
These parameters totally determine the geometry of the Universe if it
is homogeneous, isotropic, and matter-dominated. By the way, the
critical density
Most theorists believe that it is in some sense ``unlikely'' that all
three of these density parameters be of the same order, and we know
that
These three models push the observational limits.
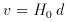
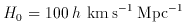
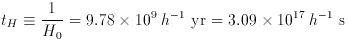
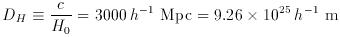
of
the Universe and the value of the
cosmological constant 
are
dynamical properties of the
Universe, affecting the time evolution of the metric, but in these
notes we will treat them as purely kinematic parameters. They can be
made into dimensionless density parameters 
M and
by
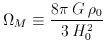
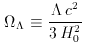
k
measures the ``curvature of space'' and can be defined by the relation
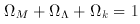
= 1
corresponds to 7.5 x
1021 h-1 M
DH-3, where M is the mass of the Sun.
M is
significantly larger than zero, so many guess that
(M, , k) = (1, 0, 0), with
(M, 1-M, 0) and
(M, 0, 1-M) tied for
second place. If = 0, then the
deceleration
parameter q0 is just half M, otherwise
q0 is not
such a useful parameter. When I perform cosmographic calculations and
I want to cover all the bases, I use the three world models
name M
Einstein-de Sitter 1 0
low density 0.05 0
high lambda 0.2 0.8