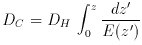A small comoving distance 
DC between two nearby
objects in the Universe is the distance between them which remains
constant with epoch if the two objects are moving with the Hubble
flow. In other words, it is the distance between them which would be
measured with rulers at the time they are being observed (the
proper distance) divided by the ratio of the scale factor of the
Universe then to now. In other words the proper distance multiplied
by (1 + z). The total line-of-sight comoving distance
DC from us
to a distant object is computed by integrating the infinitesimal
DC
contributions between nearby events along the radial ray
from z = 0 to the object.
Following Peebles (1993, pp. 310-321) (who calls the transverse comoving distance by the confusing name ``angular size distance,'' which is not the same as ``angular diameter distance'' introduced below), we define the function
which is proportional to the time derivative of the logarithm of the
scale factor (ie,
where DH is the Hubble distance defined above.
In some sense the line-of-sight comoving distance is the fundamental
distance measure in cosmography since, as will be seen below, all
others are quite simply derived in terms of it. The line-of-sight
comoving distance between two nearby events (ie, close in redshift or
distance) is the distance which we would measure locally between the
events today if those two points were locked into the Hubble flow. It
is the correct distance measure for measuring aspects of large-scale
structure imprinted on the Hubble flow, eg, distances between
``walls.''
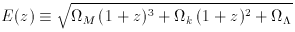
(t) / a
(t)), with z redshift and the three
density parameters defined as above. (For this reason,
H (z) = H0 E (z) is the Hubble constant
as measured by a hypothetical
astronomer working at redshift z.) Since dz = da, dz /
E (z) is
proportional to the time-of-flight of a photon traveling across the
redshift interval dz, divided by the scale factor at that time.
Since the speed of light is constant, this is a proper distance
divided by the scale factor, which is the definition of a comoving
distance. The total line-of-sight comoving distance is then given by
integrating these contributions, or
