The angular diameter distance DA is defined as
the ratio of
an object's physical transverse size to its angular size (in radians).
It is used to convert angular separations in telescope images into
proper separations at the source. It is famous for not increasing
indefinitely as z -> 
; it turns over at z ~ 1 and
thereafter more distant objects actually appear larger in angular
size. Angular diameter distance is related to the transverse comoving
distance by
(Weinberg 1972,
pp. 421-424;
Weedman 1986,
pp. 65-67;
Peebles 1993,
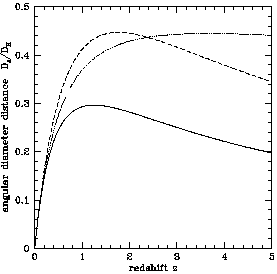
pp. 325-327). The angular diameter distance is plotted in
Figure 2.
Figure 2. The dimensionless angular
diameter DA / DH. The three curves are for
the three world models, (
There is also an angular diameter distance DA12 between two
objects at redshifts z1 and z2,
frequently used in gravitational
lensing. It is not found by subtracting the two individual
angular diameter distances! The correct formula, for
where DM1 and DM2 are
the transverse comoving distances to
z1 and z2, DH is
the Hubble distance, and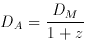
M, 
) =
(1, 0), solid; (0.05, 0) dotted; and (0.2, 0.8) dashed.
k 
0, is
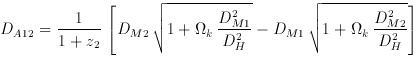
k is the curvature density parameter
(Peebles 1993,
pp. 336-337).
Unfortunately, the above formula is not correct for
k < 0 (Phillip
Helbig, 1998, private communication).