


Or, to put it another way, what distinguishes an Im galaxy with a high star formation rate, but not a starburst, from a galaxy with a low rate. Detailed studies of the stellar populations of irregulars have shown that most irregular galaxies evolve at more or less constant star formation rates with variations of factors of 2-3 in the amplitude of the rate at least over the past few Gyrs (Tolstoy 1996, Tosi et al. 1991, Greggio et al. 1993, Marconi et al. 1995). Therefore, galaxies with relatively high rates today have most likely had relatively high rates for most of their lifetime, and similarly for those forming stars at low rates (but this remains controversial). Plots of star formation rates against other global properties do not yield correlations except for those properties that would be expected to be a consequence of the level of star formation. An example of the latter is surface brightness; the higher the star formation rate per unit area, the higher the surface brightness would be expected to be. This general lack of correlations suggests that local rather than global conditions are important in setting the star formation rate.
In 1984 I came to the USNO in Flagstaff to give a talk about star formation in irregular galaxies. The next day, my host, Dave Monet, and I hiked up to the top of a local mountain. There we chatted with a national forest service employee who was scanning the surrounding region for fires and who was interested to hear that we were astronomers. Dave told him about the talk I had just given and I told him that irregulars were useful laboratories for studying star formation because they were different from spiral galaxies. The fire look-out, who apparently is an avid reader of astronomy, responded, ``But, star formation is a local process, so why would you expect star formation to be different in different galaxies?'' There are two parts to the fire look-out's question, and we will come back to the second part in a later section. But, the first premise, that ``star formation is a local process,'' does indeed seem to be borne out as the following illustrates.
Hodge & Kennicutt (1983) found
that the radial profile of H II regions
and stars was approximately the same in a sample of spiral galaxies and
concluded that there was radial ``continuity'' between current and
past star formation. Ryder & Dopita
(1994) come to a similar conclusion
from a comparison of H and I-band images of spirals. This relationship has been shown to
carry over to irregular galaxies as well.
Hunter & Gallagher (1985b)
plotted the radial brightness in B
against that in H
and I-band images of spirals. This relationship has been shown to
carry over to irregular galaxies as well.
Hunter & Gallagher (1985b)
plotted the radial brightness in B
against that in H for the
irregular galaxy NGC 4449. They found that the H
for the
irregular galaxy NGC 4449. They found that the H and B-band tracked each other
with radius very well. The H
and B-band tracked each other
with radius very well. The H luminosity shows the current star formation activity and
that in a broad-band filter such as B is related to the
star formation activity integrated over something like a Gyr
timescale (Gallagher et al.
1984). So, the conclusion was that
star formation in irregular galaxies is a local process.
luminosity shows the current star formation activity and
that in a broad-band filter such as B is related to the
star formation activity integrated over something like a Gyr
timescale (Gallagher et al.
1984). So, the conclusion was that
star formation in irregular galaxies is a local process.
Now ``local'' can have several meanings. By ``local'' one can mean
what goes on inside of a gas cloud once it forms, but here I
am using ``local'' to mean a region of a galaxy, something one to a few
kpc in size. We have now extended this to a longer
look-back time for the star formation activity in NGC 4449
using J and H images. These near-IR images are sensitive to the star formation
activity integrated over the galaxy's lifetime and show
the same general correspondence with H . In other words, the current star formation activity
throughout NGC 4449 is in keeping with the past activity at
that radius. In other irregulars that are not as busy as
NGC 4449 in terms of
star formation activity, the correspondence between H
. In other words, the current star formation activity
throughout NGC 4449 is in keeping with the past activity at
that radius. In other irregulars that are not as busy as
NGC 4449 in terms of
star formation activity, the correspondence between H and optical starlight is noisier.
In these galaxies
single star-forming regions coming and going have a larger impact on
what is observed globally and so the statistics are poorer. Nevertheless,
it seems to be true for a larger sample of irregulars that within the
statistics the time-averaged level of past star formation activity
is in keeping with the current level at that radius
(Hunter, Elmegreen, & Baker
1997; also true for Sc spirals [Kennicutt 1989])
even though the current sites of active star formation move around
within a galaxy over time (Hodge
1969, Payne-Gaposchkin 1974,
Hunter et al. 1982).
and optical starlight is noisier.
In these galaxies
single star-forming regions coming and going have a larger impact on
what is observed globally and so the statistics are poorer. Nevertheless,
it seems to be true for a larger sample of irregulars that within the
statistics the time-averaged level of past star formation activity
is in keeping with the current level at that radius
(Hunter, Elmegreen, & Baker
1997; also true for Sc spirals [Kennicutt 1989])
even though the current sites of active star formation move around
within a galaxy over time (Hodge
1969, Payne-Gaposchkin 1974,
Hunter et al. 1982).
There are still global aspects to the star formation process in the sense that large-scale processes determined the formation of irregular galaxies and the initial conditions within them that result in their slow evolution. But, given those initial global conditions, including the rotation curve and three-dimensional distribution of the gas, the star formation process responds to local conditions within the galaxy. What then might be the mechanisms that control star formation? The local equilibrium rules out processes such as infall of gas as major drivers of star formation in irregulars (Hunter & Gallagher 1985b), and we also suspect that the star formation process is not entirely stochastic and that gas distributions and velocity fields will play important roles.
There are several basic models currently in the literature that
offer some insight.One is that of gravitational stability of gas in a
thin rotating disk (Toomre 1964,
Quirk 1972). This model defines
a critical
gas density  c
above which the gas is unstable and will form clouds
that then can form stars and below which the gas is stable against the
formation of clouds. This critical gas density depends on the
velocity dispersion and the epicyclic frequency of the gas.
Kennicutt (1989) applied this
model to Sc spiral galaxies. He plotted
the ratio of the observed gas density
c
above which the gas is unstable and will form clouds
that then can form stars and below which the gas is stable against the
formation of clouds. This critical gas density depends on the
velocity dispersion and the epicyclic frequency of the gas.
Kennicutt (1989) applied this
model to Sc spiral galaxies. He plotted
the ratio of the observed gas density  g
to the model critical gas density
g
to the model critical gas density  c
as a function of radius within the galaxies.
Generally this ratio decreased with radius. Then he determined
the radius at which he could no longer detect H II regions in these
galaxies. The idea is that beyond that radius the gas is too stable
to form clouds and interior to that the gas is unstable.
For his sample of Sc spirals this ratio
c
as a function of radius within the galaxies.
Generally this ratio decreased with radius. Then he determined
the radius at which he could no longer detect H II regions in these
galaxies. The idea is that beyond that radius the gas is too stable
to form clouds and interior to that the gas is unstable.
For his sample of Sc spirals this ratio  =
=  g /
g /  c
was about 0.7 ± 0.2 at the radius where the last H II regions were seen.
So, gas at densities lower than roughly 0.7 times
the critical density was too stable to form the clouds needed for
star formation (see also Larson 1992).
c
was about 0.7 ± 0.2 at the radius where the last H II regions were seen.
So, gas at densities lower than roughly 0.7 times
the critical density was too stable to form the clouds needed for
star formation (see also Larson 1992).
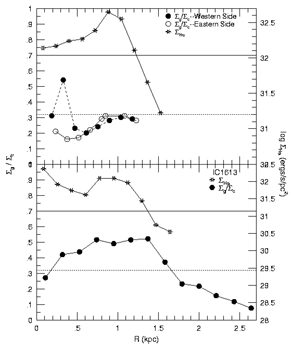
Figure 9. Radially averaged ratio  g / g /  c of observed gas
(H I + He + H2) density to critical gas density for the thin
rotating disk model. Results for two representative irregulars are taken
from Hunter & Plummer (1996) and
Baker (1997); based on
H I data taken from Skillman et
al. (1988) for Sextans A and
from Lake & Skillman (1989) for
IC 1613. Also plotted are the radially averaged
H c of observed gas
(H I + He + H2) density to critical gas density for the thin
rotating disk model. Results for two representative irregulars are taken
from Hunter & Plummer (1996) and
Baker (1997); based on
H I data taken from Skillman et
al. (1988) for Sextans A and
from Lake & Skillman (1989) for
IC 1613. Also plotted are the radially averaged
H surface brightness
which is proportional to the amount of current star formation.
The dashed line denotes the median surface brightness
which is proportional to the amount of current star formation.
The dashed line denotes the median  , the ratio , the ratio  g / g /  c at the radius of the
furthest detected H II region, in a sample of 7 irregular galaxies, and
the solid line is the average for spiral galaxies
(Kennicutt 1989). c at the radius of the
furthest detected H II region, in a sample of 7 irregular galaxies, and
the solid line is the average for spiral galaxies
(Kennicutt 1989).
|
Hunter & Plummer (1996) and
Baker (1997) have applied this
model to several irregular galaxies for which azimuthally averaged H I column
densities and rotation curves were available in the literature.
They found that generally this ratio  g /
g /  c in irregulars is everywhere less than the ratio
found by Kennicutt for spirals, and typically
c in irregulars is everywhere less than the ratio
found by Kennicutt for spirals, and typically
 is 0.3-0.5 although
there are a few exceptions (see also van Zee et al. 1996).
This is illustrated for two irregulars in
Figure 9.
We have also extended this to a sample of more distant
Im and Sm galaxies found in surveys by Schombert and collaborators
(1988,
1992; see also,
Bothun, Impey, & McGaugh 1997).
Again, this ratio is low in these systems although not
more so than in other irregulars.
At face value, this low ratio of observed to critical gas density
implies that irregulars have a much harder time forming
clouds than spirals. In fact, Larson
(1988) suggests that galaxies like
irregulars that do not have the benefit of ``swing amplification''
(a mode of gravitational instability in differentially rotating disks
[Goldreich & Lynden-Bell 1965])
will require even higher values of
is 0.3-0.5 although
there are a few exceptions (see also van Zee et al. 1996).
This is illustrated for two irregulars in
Figure 9.
We have also extended this to a sample of more distant
Im and Sm galaxies found in surveys by Schombert and collaborators
(1988,
1992; see also,
Bothun, Impey, & McGaugh 1997).
Again, this ratio is low in these systems although not
more so than in other irregulars.
At face value, this low ratio of observed to critical gas density
implies that irregulars have a much harder time forming
clouds than spirals. In fact, Larson
(1988) suggests that galaxies like
irregulars that do not have the benefit of ``swing amplification''
(a mode of gravitational instability in differentially rotating disks
[Goldreich & Lynden-Bell 1965])
will require even higher values of  g /
g /  c to form stars.
However, since stars are being formed in irregulars,
this suggests that other processes in addition to gravity are important
in facilitating cloud formation in irregulars
(for example, feedback from massive stars, random gas motions).
c to form stars.
However, since stars are being formed in irregulars,
this suggests that other processes in addition to gravity are important
in facilitating cloud formation in irregulars
(for example, feedback from massive stars, random gas motions).
Comparisons of the azimuthally-averaged
ratio of observed to critical gas densities
as a function of radius with the distribution of current
star formation (H surface
brightness profiles) often show
star formation occurring in the
regions of higher
surface
brightness profiles) often show
star formation occurring in the
regions of higher  g /
g /  c (see also van der Hulst et al. [1993]
for low surface brightness spirals, Taylor
et al. [1994] for H II galaxies, and
van Zee et al. [1996]
for another Im galaxy) although exceptions are seen.
However, usually star formation ends long before the gas densities
would suggest that it should even when the destabilization due to
the two-fluid nature of galaxies (that is, stars as well as gas)
is taken into account (Elmegreen
1995a; Hunter, Elmegreen, &
Baker 1997). Furthermore, there does not seem to be any trend of average
gas densities relative to the critical values with globally integrated
star formation rates (but see Buat
et al. [1989]).
c (see also van der Hulst et al. [1993]
for low surface brightness spirals, Taylor
et al. [1994] for H II galaxies, and
van Zee et al. [1996]
for another Im galaxy) although exceptions are seen.
However, usually star formation ends long before the gas densities
would suggest that it should even when the destabilization due to
the two-fluid nature of galaxies (that is, stars as well as gas)
is taken into account (Elmegreen
1995a; Hunter, Elmegreen, &
Baker 1997). Furthermore, there does not seem to be any trend of average
gas densities relative to the critical values with globally integrated
star formation rates (but see Buat
et al. [1989]).
A second model is that presented by Parravano (1989) and Elmegreen & Parravano (1994) in which they explore the pressure in a galactic disk and what is necessary for the formation of cold, dense clouds. They have suggested that low surface brightness galaxies have reduced star formation rates because the pressure in their disks is below the minimum pressure needed to enable the formation of dense molecular clouds that form stars. Hunter & Plummer (1996) have compared this model to the irregular Sextans A. The model is put in terms of the thermal pressure in the galactic disk and the stellar radiation field in the disk, quantitites whose observational determinations are fraught with difficulties, and agreement of the model with what is observed in Sextans A is mixed. The inner part of the galaxy that is forming stars lies just above the pressure threshold, but then so does a portion of the outer part of the galaxy which is not forming stars. Similar results are found for a larger sample of irregulars by Hunter, Elmegreen, & Baker (1997) although Young & Lo (1996) find that star-forming regions in Leo A are only associated with a cold component of the H I gas in that galaxy.
Neither of these two models is entirely satisfactory, however.
For a rotating gas disk, for example, complications such as
the presence of dark matter (Elmegreen et al. 1996)
and the extra thickness of disks (Romeo 1992) have not been
adequately explored. The thicker disks of irregulars
(Hodge & Hitchcock 1966,
van den Bergh 1988, see also
Puche et al. 1992)
should serve to stabilize the gas, lowering  . In addition the lack of
shear in the ISM to aid in disrupting clouds could make star formation
easier for a given
. In addition the lack of
shear in the ISM to aid in disrupting clouds could make star formation
easier for a given  relative to the situation in spirals
(Kenny, Carlstrom, & Young 1993).
Furthermore, kinematics in Im systems are often dominated
by random gas motions which can contribute significantly to the pressure
(for example, Gottesman & Weliachew
1977, Tully et al.
1978, Huchtmeier et al.
1981, Sargent et al. 1983,
Lo et al. 1993,
Feitzinger et al. 1981),
and in some cases rotation can be insignificant compared to random
motions (Young & Lo 1996).
In addition in physically small galaxies like these, single giant
star-forming regions can dominate and it seems likely that the modifications
of the ISM by concentrations of massive stars are likely to play
a large role in feedback processes including facilitating further cloud
formation. Thus, multiple factors are likely to be important in regulating
cloud/star formation, and current models do not include this
complexity.
relative to the situation in spirals
(Kenny, Carlstrom, & Young 1993).
Furthermore, kinematics in Im systems are often dominated
by random gas motions which can contribute significantly to the pressure
(for example, Gottesman & Weliachew
1977, Tully et al.
1978, Huchtmeier et al.
1981, Sargent et al. 1983,
Lo et al. 1993,
Feitzinger et al. 1981),
and in some cases rotation can be insignificant compared to random
motions (Young & Lo 1996).
In addition in physically small galaxies like these, single giant
star-forming regions can dominate and it seems likely that the modifications
of the ISM by concentrations of massive stars are likely to play
a large role in feedback processes including facilitating further cloud
formation. Thus, multiple factors are likely to be important in regulating
cloud/star formation, and current models do not include this
complexity.
In summary, it seems that star formation is largely a local (that is, regional) process in the sense that it is radially the same today as it has been historically over large time-scales. In irregulars star formation is likely to be regulated by a combination of processes including gravitational instabilities due to the gas density, thermal pressure within the disk, and modifications of the ISM by massive stars. In irregular galaxies, perhaps more so than in other larger systems, random gas motions and feedback from massive stars may play large roles.