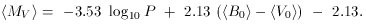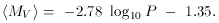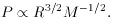
The luminosity of the star, L, is correlated with its mass due to the strong density and temperature dependences of the energy generation equations:
However, luminosity is
also determined by the stellar radius and effective temperature, T, by
so we can
eliminate mass as a variable and the period is determined from two parameters:
luminosity and temperature. The corresponding observational quantities are
magnitude and color index.
The period-luminosity-color (P-L-C) relation is an equation for a
plane. Cepheid variables are found only in the swath of the plane where
stars are pulsationally unstable (and where real stars are actually
found due to evolution!).
Projections of this plane along each axis result in
1) the color-magnitude diagram, 2) the period-color diagram, and 3) the
period-luminosity diagram. This is illustrated in
Figure 3, where the
data on galactic calibrating Cepheids is taken
from Table 2 of
Feast and Walker
(1987).
Note that
changing the boundaries of the allowed region of instability in the plane
does nothing to reduce the quality of the P-L-C fit, but will change the
widths of the distributions in all the projected planes. Incomplete filling
of the instability strip by evolutionary tracks can therefore affect
distance determinations using the P-L relation, but will not
affect distances
derived from a P-L-C relation. (The reader should note the similarities
between the P-L-C plane and the so-called 'fundamental plane' of the
Dn -
Recent work on Galactic and LMC Cepheids by
Fernie (1990) and
Mateo et al. (1990)
has demonstrated that
the instability strip does not seem to have a constant width in color.
Rather, the instability strip is better described by a wedge in the
color-magnitude diagram opening at (B - V) = 0.4,
MV = -2 mag with
blue and red edges proceeding toward (B - V) = 0.6,
MV = -5 mag, and
(B - V) = 1.1, MV = -5 mag, respectively. This
is most likely due to the
filling of the instability region by evolution - the existence
of pulsating
The values of the coefficients of the P-L-C are still a topic of
active discussion (especially with regard to metallicity dependence). However,
a representative P-L-C relation from
Feast and Walker
(1987) is:
The bracket notation indicates flux-weighting and the zero subscript
indicates a dereddened magnitude. Similarly, a representative P-L
relation from the same source is:
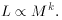
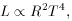
 relation.)
relation.)
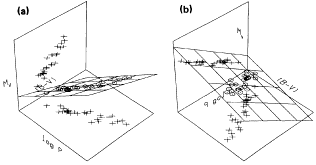
Figure 3. Three-dimensional representations of the P-L-C
relation given in the text with the points from Table 2 of
Feast and Walker
(1987)
plotted. In (a) the projections onto the color-magnitude
and period-color diagram are shown. The viewpoint in (b) has been chosen
to highlight the period-luminosity and period-color projections.
 Scuti stars and
white dwarfs is evidence that the
instability strip exists at lower luminosities.
Scuti stars and
white dwarfs is evidence that the
instability strip exists at lower luminosities.