(6)
(where A is a normalization factor representing the peak
population of globular clusters in the galaxy) does an
excellent job of describing the GCLF in all galaxies
studied to date. The log-normal fitting function
gives a convenient way to parameterize the data and to
intercompare the GCLFs from different galaxies. For
the nearest rich systems of galaxies containing giant
ellipticals (the Virgo and Fornax clusters) the deepest
limits achieved at present reach to just about 1
 fainter than the turnover
(Harris et al. 1991).
fainter than the turnover
(Harris et al. 1991).
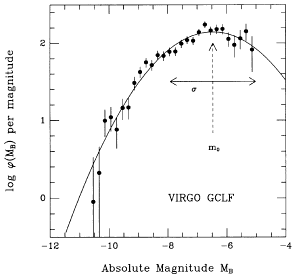
Figure 7. The luminosity function for the globular clusters in
four Virgo ellipticals combined
(NGC 4365,
4472,
4486,
4649), from
Harris et al. (1991).
This composite GCLF was constructed from a total
sample of about 2000 clusters brightes than B = 26.2 (the
vertical scale units shown are arbitrary). Here  is the relative number of clusters per
unit magnitude interval, plotted against absolute magnitude
MB assuming d(Virgo) is the relative number of clusters per
unit magnitude interval, plotted against absolute magnitude
MB assuming d(Virgo)  17 Mpc. A Gaussian interpolation
curve is superimposed, with a ``trnover'' or peak indicated by the
dashed arrow (m0), and a standard deviation 17 Mpc. A Gaussian interpolation
curve is superimposed, with a ``trnover'' or peak indicated by the
dashed arrow (m0), and a standard deviation  = 1.45 mag. = 1.45 mag.
|
The actual use of the GCLF method, in its simplest form,
goes as follows. The `standard candle' is essentially the
magnitude of the turnover, m0.
The goal in observing any distant galaxy is then
to obtain photometry of its halo clusters which reaches
sufficiently faint to estimate m0 accurately.
In practice, the GCLF is normally found as
the residual excess of starlike objects (see
Figure 6),
after a background LF for the field has been subtracted
and photometric detection incompleteness at the faintest
levels has been accounted for. By fitting an analytic
interpolation function (such as the Gaussian model above)
to the observed data, or else by using a maximum-likelihood fit to the
total observed LF (GCLF plus background), the
curve parameters (A, m0,  ) and their internal
uncertainties can be estimated
(van den Bergh et
al. 1985;
Pritchet and van
den Bergh 1985b;
Hanes and Whittaker
1987;
Harris et al. 1991).
Adopting an absolute
magnitude M0(turnover), and any necessary correction for
foreground reddening, immediately yields
the distance modulus.
) and their internal
uncertainties can be estimated
(van den Bergh et
al. 1985;
Pritchet and van
den Bergh 1985b;
Hanes and Whittaker
1987;
Harris et al. 1991).
Adopting an absolute
magnitude M0(turnover), and any necessary correction for
foreground reddening, immediately yields
the distance modulus.
If the limiting magnitude of the photometry goes
clearly past the turnover as in the example of
Figure 7, both
m0 and  can
be solved for simultaneously. Ideally,
the uncertainty e (m0) would be equal to
can
be solved for simultaneously. Ideally,
the uncertainty e (m0) would be equal to  /
/  N,
which for a sample size N of several hundred or more clusters
should be ± 0.1 mag or smaller. In practice, the extra
noise introduced by the background LF subtraction
and completeness corrections, and the uncertainty in
N,
which for a sample size N of several hundred or more clusters
should be ± 0.1 mag or smaller. In practice, the extra
noise introduced by the background LF subtraction
and completeness corrections, and the uncertainty in  itself, lead to best-case results near
e (m0)
itself, lead to best-case results near
e (m0)  ± 0.2 mag for a single galaxy. However, if the limit of the data
falls at or a bit short of the turnover, then the fitted solutions
for m0 and
± 0.2 mag for a single galaxy. However, if the limit of the data
falls at or a bit short of the turnover, then the fitted solutions
for m0 and  become strongly correlated
(Hanes and
Whittaker 1987).
It is still possible to estimate m0 to
a typical precision of ± 0.3 mag, but only by performing a
restricted function fit with an assumed, externally-known
value of
become strongly correlated
(Hanes and
Whittaker 1987).
It is still possible to estimate m0 to
a typical precision of ± 0.3 mag, but only by performing a
restricted function fit with an assumed, externally-known
value of  (hence the importance
of the basic premise that the GCLF parameters are the same for galaxies
of the same type; see Sec. 4.4). An
alternative is to adopt the
well-defined Virgo GCLF
(Figure 7) as a fiducial
function and to match any other galaxy to it by adjusting its distance
relative to Virgo until a best fit is achieved.
(hence the importance
of the basic premise that the GCLF parameters are the same for galaxies
of the same type; see Sec. 4.4). An
alternative is to adopt the
well-defined Virgo GCLF
(Figure 7) as a fiducial
function and to match any other galaxy to it by adjusting its distance
relative to Virgo until a best fit is achieved.
The range of applicability of the GCLF method, and its basic
strengths, are readily summarized.
(1) The GCLF works by
far the best in giant E galaxies, which contain the
largest globular cluster populations (N  1000 is
observationally feasible in such galaxies).
On the other hand, the GCLF method is immensely more difficult
to employ in late-type galaxies (Sc, Sd, Irr),
and so in most cases it is difficult to match the GCLF
distance scale directly with any of the Population I
techniques.
1000 is
observationally feasible in such galaxies).
On the other hand, the GCLF method is immensely more difficult
to employ in late-type galaxies (Sc, Sd, Irr),
and so in most cases it is difficult to match the GCLF
distance scale directly with any of the Population I
techniques.
(2) Because the clusters are nonvariable
objects, they do not require repeated or carefully scheduled
time-series observations. Telescope time is thus employed efficiently.
(3) Because it applies to
objects in the halos of large galaxies, the method
is free of a host of observational problems
that affect all Population I standard candles, such as internal
reddening differences, crowding and source confusion,
and inclination-angle corrections.
(4) The distance range of the primary GCLF method is
set by the limiting magnitude at which the turnover M0 is
still detectable. With current ground-based capabilities, the
limit should be near d  50 Mpc (Harris
1988a).
50 Mpc (Harris
1988a).



 (m) of globular
clusters as a
function of magnitude m) for the Virgo giant
ellipticals. The functional shape of
(m) of globular
clusters as a
function of magnitude m) for the Virgo giant
ellipticals. The functional shape of  (m) is
characterized by two simple parameters: the magnitude level
or turnover point (m0)
where the population of clusters reaches a maximum; and the
dispersion (
(m) is
characterized by two simple parameters: the magnitude level
or turnover point (m0)
where the population of clusters reaches a maximum; and the
dispersion ( (m)
or standard deviation of the distribution.
As an empirical curve, the observations show that a
Gaussian or log-normal function
(m)
or standard deviation of the distribution.
As an empirical curve, the observations show that a
Gaussian or log-normal function



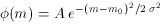

 17 Mpc. A Gaussian interpolation
curve is superimposed, with a ``trnover'' or peak indicated by the
dashed arrow (m0), and a standard deviation
17 Mpc. A Gaussian interpolation
curve is superimposed, with a ``trnover'' or peak indicated by the
dashed arrow (m0), and a standard deviation  N,
which for a sample size N of several hundred or more clusters
should be ± 0.1 mag or smaller. In practice, the extra
noise introduced by the background LF subtraction
and completeness corrections, and the uncertainty in
N,
which for a sample size N of several hundred or more clusters
should be ± 0.1 mag or smaller. In practice, the extra
noise introduced by the background LF subtraction
and completeness corrections, and the uncertainty in  1000 is
observationally feasible in such galaxies).
On the other hand, the GCLF method is immensely more difficult
to employ in late-type galaxies (Sc, Sd, Irr),
and so in most cases it is difficult to match the GCLF
distance scale directly with any of the Population I
techniques.
1000 is
observationally feasible in such galaxies).
On the other hand, the GCLF method is immensely more difficult
to employ in late-type galaxies (Sc, Sd, Irr),
and so in most cases it is difficult to match the GCLF
distance scale directly with any of the Population I
techniques.