5.3 Calibration

The calibration can be effected in two ways: (1) using Galactic novae (in which case the use of the MMRD relation is a primary distance indicator, calibrated using geometrical techniques); or (2) using novae in M31 (in which case the distance scale is tied to the distance of M31).

The Cohen (1985) MMRD relation for Galactic novae is given by:

(7)

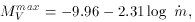
where mdot is the mean rate of decline (in mag d^-1) over the first 2 magnitudes. The mean scatter around this relation is ± 0.52 mag (1 ) for the high quality subset of Cohen's data. The data and fit are shown in Figure 9. A slightly different result is obtained if the Galactic data are corrected for the constancy of M_B 15 days after maximum light (Buscombe and de Vaucouleurs 1955). In principle such a correction removes systematic errors in the absolute magnitudes, and results in a tighter MMRD correlation ( 0.47 mag for all objects).

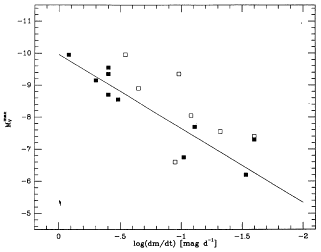
Figure 9. Maximum magnitude-rate of decline relation for Galactic novae observed by Cohen (1985). Closed symbols represent the novae designated ``high quality'' by Cohen; the solid line [Eq. (7)] is a least-squares fit to the high-quality data.

An alternate calibration of the MMRD relation is obtained by studying novae in the nearby spiral galaxy M31. The properties of the nova system in M31 have been reviewed by Ciardullo et al. (1987) and by Capaccioli et al. (1989). Only about 1/3 of the known novae in M31 have sufficient information in their light curves to be useful in determining the MMRD relation, and only about 1/4 of these possess good quality light curves with a well-observed maximum and rate of decay. The M31 MMRD relation is shown in Figure 10. The 1 scatter around the mean relation depends on the subset of data chosen, and is in the range 0.20 - 0.28 mag (cf. Capaccioli et al. 1989, van den Bergh and Pritchet 1986).

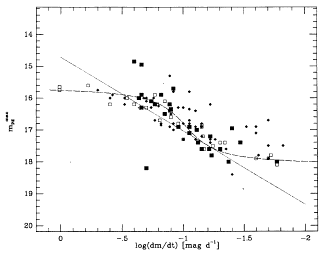
Figure 10. Maximum magnitude-rate of decline relation for novae in M31. The data (from several sources) have been taken from Table VI of Capacioli et al. (1989). Solid squares: high-quality data; open squares: medium-quality data; dots: low-quality data. The solid line represents the Galactic calibration (Fig.9), shifted by (m - M)B = 24.6, and transformed to the mpg system as described in the text. The dashed line represents the Capacioli et al. analytical fit to the M31 data.

To compare the M31 MMRD data with the mean Galactic MMRD, we assume (m - M)_B 24.6 for M31 (e.g., Pritchet and van den Bergh 1987b and references therein), (B - V)^max 0.23 (van den Bergh and Younger 1987), and (m_pg - B) -0.17 (Arp 1956). With these assumptions, it can be seen from Figure 10 that the agreement between the Galactic and M31 MMRD relations is not good: the flattening observed in the M31 MMRD relation for bright and faint novae is not seen for Galactic novae. In addition, there appears to be a systematic offset of about 0.3 mag between the two MMRD relations, in the sense that Galactic novae are fainter than M31 novae. (This offset would increase to ~ 0.5 mag if the mean internal absorption for M31 novae were 0.2 mag [van den Bergh 1977, Capaccioli et al. 1989]. However, we note that Ford and Ciardullo [1988] have failed to find any systematic difference in the MMRD relation for novae close to and far from obvious dust patches in the bulge of M31.)

What could cause these differences between the Galactic and M31 MMRD relations? The flattening at faint magnitudes in the M31 MMRD relation may be due to Malmquist bias: in the presence of a magnitude limit, only the brightest novae will be detected. Whether or not this flattening is real has little effect on distance determinations outside the Local Group, because it is predominantly the most luminous novae that are detected at large distances. The flattening of the M31 MMRD relation for luminous novae is a more difficult problem. If one aligns the MMRD relations for Galactic and M31 novae in the ``linear'' (-1.3 log mdot -0.7) regime, then the luminous (log mdot -0.6) Galactic novae lie an average of ~ 0.8 mag above the M31 MMRD relation. One possible explanation for this is that maximum light for M31 novae is not as well sampled as it is for Galactic novae; this is particularly apparent in the light curves of Arp 1 and Arp 2 (Arp 1956).

The shift of the Galactic and M31 MMRD relations relative to each other seems to imply that the true distance modulus of M31 is 0.3 mag less than the value obtained with ``quality'' distance indicators (e.g., RR Lyrae stars, IR observations of Cepheids). However, Capaccioli et al. (1989) have demonstrated that this discrepancy vanishes if a different sample of objects is chosen to define the Galactic MMRD, and if uncorrected M_V^max values are used for the Galactic nova sample (instead of M_V values corrected for the Buscombe - de Vaucouleurs effect). It is also worth noting that the theoretical MMRD (Shara 1981b) possesses a flatter slope than that observed for Cohen's (1985) data on Galactic novae, and hence provides a better overall fit to the S-shaped MMRD relation observed for M31 novae.

Finally, it should be noted that the Galactic MMRD relation is defined with far fewer objects than is the case for M31; furthermore, the overall quality of the Galactic data (as demonstrated by the scatter in the MMRD relation) is considerably lower than for M31, probably due to such effects as uncertain Galactic absorption, and due to the assumption of spherical symmetry that is inherent in Cohen's application of the expansion parallax technique (Ford and Ciardullo 1988). In fact, the offset between the Galactic and M31 MMRD relations is almost exactly what would be expected if the prolate geometry of nova shells is not taken into account when applying the expansion parallax technique (Ford and Ciardullo 1988).

In view of all of the above, it seems somewhat safer to employ the M31 MMRD relation as the calibrator for the extragalactic distance scale. This makes the distance scale dependent on an assumed distance to M31. However, Pritchet and van den Bergh (1987b) and van den Bergh (1989) show that there is concordance in most distance estimates for M31 (except those derived using novae!); using the M31 calibration is therefore a more prudent approach at the present time.