 -16.0,
the total number of calibrators would be 15.
-16.0,
the total number of calibrators would be 15.



7.4 Absolute Calibration
At the time of Tully and Fisher (1977), only two local calibrating galaxies had moderately secure distance determinations, M31 and M33. Subsequently, there has been some debate as to the distance of M33 (see Sec. 3). Pierce and Tully (1988) presented an absolute calibration based upon CCD photometry of M31, M33, and NGC 2403 in the B and R bands with I band data provided only for the latter. However, Burstein and Raychaudhury (1989) pointed out some significant problems with the Pierce and Tully photometry of M31. This was a particular concern given the small number of local calibrators available.
Recently, the situation has changed dramatically,
with extensive CCD photometry of Cepheids and RR Lyrae
variables in nearby galaxies. There are now reliable distance estimates
to three systems in or near the Local Group (M31, M33, NGC 3109),
two systems in
the M81 Group (M81 and NGC 2403), and one galaxy in the Sculptor Group
(NGC 300). If, in addition to these systems, we
could make use of the other
members of the M81 and Sculptor groups with MB  -16.0,
the total number of calibrators would be 15.
-16.0,
the total number of calibrators would be 15.
Pierce and Tully (1992a) have recently completed an analysis of the absolute calibration of the TF relations which addresses many of the concerns expressed by Burstein and Raychaudhury (1989). The relations are shown as the upper sequence of panels in Figure 11. The solid points represent those systems with individual distance estimates provided by Cepheids and/or RR Lyrae variables, while the open symbols represent additional members of the M81 and Sculptor groups (square and triangles, respectively). These are assumed to be at a mean distance given by those systems with individual distance estimates. The distribution of the additional members of the M81 Group is consistent with a small dispersion, implying a small line-of-sight depth for the group. The large dispersion for members of the Sculptor Group is consistent with previous suggestions of significant line-of-sight depth for the group (e.g., de Vaucouleurs and Davoust 1980). The dispersions are ~ 0.20 mag for the systems with individual distance estimates, implying a precision in distance estimates from the TF relations of ~ 10% for an individual galaxy.
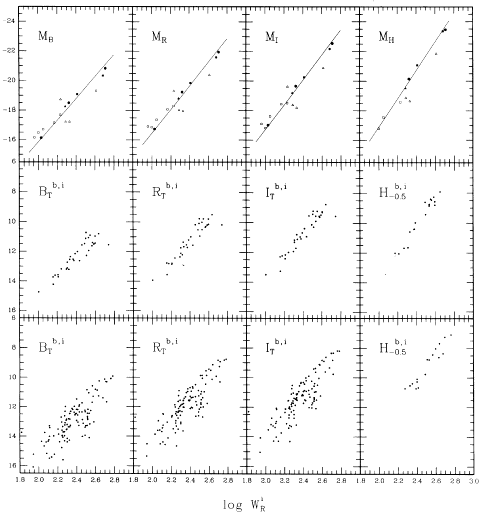
Figure 11. B-, R-, I-, and H-band Tully-Fisher relations for the Local Calibrators (top), Ursa Major cluster members (middle), and Virgo cluster members (bottom). It is apparent from the figures that the slope of the relations increases going to longer wavelengths and the dispersion decreases. The variation in slope is thought to arise from the differing contributions to the observed bandpass made by greater fraction of young stars found in the lower-luminosity systems. The smaller dispersion at longer wavelengths is likely due to a reduction in the sensitivity of these effects, as well as those expected from extinction variations. Nothe the much larger dispersion found for the Virgo cluster data. |
On the other hand, Sandage (1988), Kraan-Korteweg et al. (1988), and Tammann (1988) suggest that the intrinsic dispersion of the TF relations may be as large as 0.7 mag (see Sec. 7.5). However, the data shown as the upper sequence of Figure 11 are not consistent with that result, nor is Freedman's (1990) demonstration that the intrinsic dispersion is small for the IRTF relations.
From the six local calibrating galaxies currently with individual distances the zero point of the calibration is established to an uncertainty of 0.08 mag (Freedman 1990; Pierce and Tully 1992a). The distances assumed for the local calibrators are all estimated relative to the distance of the LMC, which is tied to the Galactic calibration of Cepheids and RR Lyraes. The distance of the LMC is uncertain to ~ 7% (e.g., Feast and Walker 1987) and so the primary source of error in the TF calibration lies with the Galactic calibration of the Cepheid P-L and P-L-C relations.
Pierce and Tully (1992a) find a significant systematic color difference between field (i.e., the ``local calibrators'') and cluster galaxies (see also Holmberg 1958). This results in a systematic variation in the estimated distances with bandpass. A small (~ 0.25 mag) correction is necessary in the B-band in order to produce consistent distance estimates over all bandpasses and environments. The resulting calibration is given by:
where the correction factors 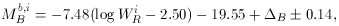
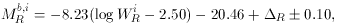
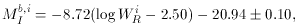
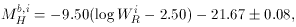
 B = 0.25 and
B = 0.25 and  R = 0.06 are
required for statistically consistent distances between the different bands
for ``cluster galaxies''. The corrections for ``field-galaxies'' should be
zero. The existence of a ``color correction'' diminishes the
utility of the B-band relation and implies that longer wavelength
bandpasses produce more reliable distance estimates. Note that
these calibrations apply only to the
Tully and
Fouqué (1985)
prescriptions for extinction and line-width corrections.
R = 0.06 are
required for statistically consistent distances between the different bands
for ``cluster galaxies''. The corrections for ``field-galaxies'' should be
zero. The existence of a ``color correction'' diminishes the
utility of the B-band relation and implies that longer wavelength
bandpasses produce more reliable distance estimates. Note that
these calibrations apply only to the
Tully and
Fouqué (1985)
prescriptions for extinction and line-width corrections.