Historically, one of the driving motivations behind attempts to measure
the diffuse
background radiation at far-ultraviolet wavelengths has been the
realization that such
observations could potentially reveal the existence of a cosmologically
significant (
b
1), "lukewarm" (103 K < T < 106 K)
intergalactic medium (cf.
Kurt & Sunyaev 1967;
Davidsen, Bowyer &
Lampton 1974;
Paresce & Jakobsen 1980).
If a baryonic intergalactic medium (IGM) does exist, standard Big Bang
nucleosynthesis
calculations predict that it must consist primarily of a mixture of
90% hydrogen
and 10% helium atoms. The
dominant emission from such a mixture at temperatures
between T
103 K and T
106 K is recombination and collisionally excited line
radiation in the HI and HeII
Ly
lines at
l = 1216Å and
l = 304Å,
respectively.
This line radiation, smeared by the redshift, will give rise to a
diffuse background at
wavelengths
l of
intensity (1)
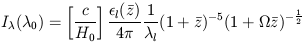
| (1) |
where 0
l is the observed
wavelength, H0 is the Hubble constant and
l(z) is the
line volume emissivity (in units of photons s-1
cm-3) evaluated at the appropriate
redshift,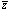 
=
0 /
l - 1 (see the
Appendix for a derivation of this expression). In the
case of a smooth IGM emitting through recombination or collisional
excitation, where
the emission goes as density squared, the line emissivity can be written
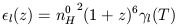
| (2) |
where n0H = 7.8 x 10-6
b
h2 cm-3 is the IGM hydrogen density at
z = 0,
b the
baryonic IGM contribution to the cosmological density parameter,
H0 = 100h km s-1
Mpc-1, and
l(T) is a
suitably normalized emission coefficient.
Figure 1 shows the run of
l(T) as a
function of temperature for a cosmological
mixture of hydrogen and helium in collisional and thermal
equilibrium. It is seen
that collisionally excited emission in the HI and HeII
Ly lines is especially intense
near the two "thermostat" temperatures T
2 x 104 K and
T 8 x 104 K,
i.e. at
the temperatures at which the dominant ionization states change from HI
to HII and
HeII to HeIII, respectively. If, following recombination, the IGM was
re-heated and
re-ionized by dissipative processes, such as shock heating, the gas
would have had to
pass through these two temperatures. Depending on the redshift and
duration of the
re-heating process, the IGM emission could give rise to observable
redshifted Ly and
HeII 304Å spectral
signatures in the ultraviolet background. Several detailed IGM
models giving rise to such features can be found in the literature
(Weymann 1967;
Sherman 1979,
1982).
|
Figure 1. Lower frame: Ionization structure
of a cosmological mixture of hydrogen
and helium in collisional equilibrium as a function of
temperature. Upper frame:
Corresponding emissivity per hydrogen atom of collisionally excited HI
and HeII Ly |
Of course, the intergalactic medium is not only constrained by limits on
its possible
emission, but also by its possible absorption. By far the most stringent
limit on the IGM comes from the classical
Gunn & Peterson (1965)
test, which severely constrains
the density of intergalactic neutral hydrogen at high redshift,
nHI(z), from the observed
lack of an intense redshift-smeared
Ly absorption trough seen just
shortward of emitted
Ly in the spectra of high
redshift quasars:
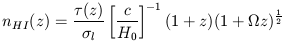
| (3) |
In this expression, 
(z) is
the optical depth of the absorption and
l =
l
(
e2) /
(me c2) fij =
4.5 x 10-18 cm2 is the integrated
Ly absorption cross
section. Both ground-based
(Steidel & Sargent 1987)
and IUE observations
(Kinney et al. 1991)
of the spectra of
quasars show no signs of absorption troughs over the redshift range 0 <
z < 4 at the
(z)
0.1 level. The
corresponding upper limit on the intergalactic neutral hydrogen
density is of order nHI(z)
10-12
cm-3. This stringent limit on the residual neutral
hydrogen component of the IGM (and its HeI equivalent;
Green et al. 1980;
Reimers et al. 1989,
1992;
Tripp, Green & Bechtold
1990;
Beaver et al. 1991)
implies that the
IGM - if it exists at all - must be highly ionized and have a
temperature greater than
T 105 K
(compare lower frame of Figure 1).
Alternatively, if photoionization, due for example to the integrated
ionizing flux of
quasars, is the process responsible for re-ionizing the IGM, then the
IGM will still emit primarily in the HI and HeII
Ly lines, albeit somewhat less
efficiently (Figure 1). On
the other hand, since the Gunn-Peterson test suggests that the IGM is
transparent, the
redshifted ionizing radiation source itself should be directly
observable in the ultraviolet
background. Absolute measurements of the ultraviolet background
intensity can therefore
in principle be used to derive the maximum IGM density that can be photoionized
by the observed flux to the level required by the Gunn-Peterson
test. However, the
available observational limits on the extragalactic UV background
intensity are generally
far brighter than anticipated for realistic intergalactic fluxes and the
corresponding
constraints placed on the IGM density from the UV background
observations are therefore not particularly confining, i.e. typically
2b
h3
102.
The dramatic developments that have taken place during the last decade in the
new field of quasar absorption lines - which can be regarded as the
"high resolution"
refinement of the classical Gunn-Peterson test - call for the above
considerations to be
revisited. The discovery of the dense "Lyman forest" of weak
Ly absorption lines seen
in the spectra of all quasars has revealed the existence of a highly
clumped component
of the IGM consisting of an abundant and evolving population of
intergalactic clouds
of possibly primordial gas. Surveys of the more massive metal-containing
absorption
systems associated with galaxies have also led to new understandings
concerning the
transparency of the universe in the ultraviolet out to large redshift.
2.1 Quasar Absorption Lines in Brief
In the following, a few key results of quasar absorption line studies of particular relevance for the topic of the diffuse ultraviolet background are briefly highlighted. A series of excellent and more comprehensive reviews that do the far-reaching topic far better justice can be found in the compilation of Blades, Turnshek & Norman (1988).
If classified according to their HI column density, there are two
classes of intervening
quasar absorption line systems: the numerous "Lyman forest" systems,
whose column densities fall in the range NHI
1013 -
1017 cm-2 and the scarcer, but denser, "Lyman
limit" systems having column densities NHI
1017 -
1022 cm-2. Lyman limit systems
nearly always show matching absorption from heavy elements, and are
therefore thought
to be associated with the gaseous halos of galaxies. The Lyman forest
systems, on the
other hand, show little or no evidence for heavy elements and are
therefore believed to
be due to intergalactic clouds of possibly primordial material.
The Lyman forest systems are extremely numerous and evolve rapidly with redshift. Their line-of-sight density evolution is usually parameterized in the form (Sargent et al. 1980; Murdoch et al. 1986; Hunstead 1988)
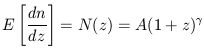
| (4) |
with A 10 and
2 - 3. Lyman limit absorbers
are roughly ten times scarcer
(A 1) and evolve less
rapidly (
1) than Lyman forest systems
(Tytler 1982;
Bechtold et al. 1984;
Lanzetta 1988;
Sargent, Steidel &
Boksenberg 1989;
Bahcall et al. 1993).
The column density spectrum of both classes of absorber is approximately a
power law, dP / dNH
N-sH, with index s
1.2 - 1.6
(Tytler 1988).
The fact that
the detailed statistics of the various types of HI containing quasar
absorption systems
are now reasonably well known permits a re-assessment of the question of
the overall transparency of the UV universe out to high redshift
(Section 2.3). These results have
important implications for the interpretation of the UV background.
Of special relevance for the topic at hand is that the Lyman forest
clouds are believed
to be kept highly photoionized by a metagalactic flux of ionizing
radiation. One key
piece of evidence for this is found in the so-called "proximity effect"
(Carswell et al. 1982;
Murdoch et al. 1986;
Bajtlik, Duncan &
Ostriker 1988;
Lu, Wolfe & Turnshek
1991).
As the emission redshift is approached, the Lyman forest absorbers in a given
quasar show a gradual under-density of absorbers with respect to the
global density
given by equation (4). This effect is interpreted as being caused by the
radiation field
of the background quasar enhancing the total ionizing flux above the
metagalactic
level. Since the quasar flux can be estimated from the magnitude and
spectrum of the
quasar, an estimate of the background metagalactic ionizing background
intensity can
be derived from the measured contrast of the proximity effect. Through
this technique
one infers that the intergalactic ionizing background in the redshift
range 1.7 z
3.8
is consistent with an
I
-,
0.5 power law with intensity
at the Lyman limit
of order IH
10-21 ergs s-1
cm-2 sr-1 Hz-1.
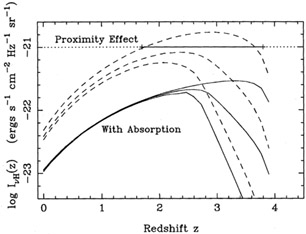
The origin of this ionizing flux is a topic of some debate (Bechtold et al. 1987; Miralda-Escudé & Ostriker 1990, 1992; Madau 1992). One obvious candidate is the integrated flux from quasars. However, only by pushing current uncertainties in our knowledge of the quasar luminosity function and evolution can the intensity required by the proximity effect barely be approached (Bajtlik et al. 1988; Lu et al. 1991; Meiksin & Madau 1993). Moreover, taking into account absorption from the Lyman forest and Lyman limit systems themselves (Section 2.3), worsens the discrepancy further by a factor of 4-5 (Figure 2). Several authors (Bechtold et al. 1987; Miralda-Escudé & Ostriker 1990, 1992; Songaila, Cowie & Lilly 1990) have suggested that an alternative candidate may be radiation from primordial galaxies. Regardless of its origin, this estimate of the ionizing flux at high redshift has important implications for the possible contributions to the extragalactic UV background from a photoionized IGM.
A final relevant constraint stemming indirectly from the quasar absorption line
studies concerns the information on the properties any pervasive IGM gas
surrounding
the Lyman forest clouds that result from considerations of Lyman forest
cloud confinement and survival
(Ostriker & Ikeuchi 1983;
Ikeuchi & Ostriker 1986).
The classical
Gunn-Peterson test limits, combined with constraints on cloud/IGM
pressure and cloud
lifetimes to evaporation, generally constrain the ambient IGM to have at
density corresponding to
b
10-1 and a
temperature T
105 K. These constraints also translate
into limits on possible IGM emission contributions to the UV background.
|
Figure 2. Predicted integrated ionizing background due to quasars for several quasar evolution models. The upper dashed curves show the integrated background intensity at the Lyman limit as a function of redshift according to the model of Bajtlik, Duncan & Ostriker (1988). The lower full curves show the same fluxes attenuated by the accumulated Lyman continuum absorption from the Lyman forest and Lyman limit classes of quasar absorption line systems (see Section 2.4). The background level required to explain the proximity effect is also indicated. |
2.2 Redshifted Lyman Alpha Emission from the IGM Revisited
Diffuse emission in Ly
1216Å from the IGM at
redshifts 0 z
0.7 will give rise
to diffuse background radiation at far-UV wavelengths
1200 - 2000 Å. Two emission
processes could produce such diffuse
Ly radiation: radiative
recombination in case of
a photoionized IGM, and collisional excitation in the case of a
shock-heated IGM.
As mentioned in Section 2.1, the Lyman forest clouds
and the smooth ambient
IGM are believed to be held highly photoionized by a metagalactic
ionizing radiation
field, presumably due to the integrated light of quasars and primeval
galaxies. What
is the possible contribution to the UV background from redshifted
Ly recombination
emission from this gas?
Consider first the case of recombination radiation from a smooth photoionized IGM. The line emissivity to be inserted into equation (1) is (Osterbrock 1989)
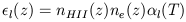
| (5) |
where l
2 x 10-13
cm3 s-1 is the effective
Ly recombination coefficient,
and nHII
and ne are the proton and electron density in the
gas. With an I
- ionizing background of average intensity
IH(z) at the Lyman limit, the equation
for hydrogen photoionization equilibrium is
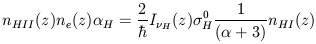
| (6) |
where H2
3 x 10-13
cm3 s-1 is the total recombination coefficient and
0H = 6.3 x
10-18 cm2 is the HI cross section at the Lyman
limit. Combining equations (5) and (6)
with the expression (3) for nHI from the Gunn-Peterson
test and inserting into equation
(1) leads to the following expression for the intensity of the resulting
redshift-smeared
Ly background due to
recombination emission
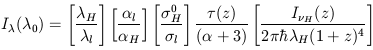
| (7) |
In this expression, the last factor in brackets is simply the intensity
of the ionizing
flux, IH(z) converted to suitable units and
redshifted to zero redshift; that is, the
background intensity that would be seen today if the ionizing flux
propagated freely
from redshift z. Since the product of the remaining factors in
equation (7) is of order
unity or less, this equation is merely reminding us that since
l /
H
0.7
Ly photons
are emitted per photoionization event, the intensity of the resulting
redshift-smeared
Ly recombination background can
never be greater than that of the ionizing input
flux itself. This principle of photon conservation, of course, applies
equally well in
the clumped case. The equivalent expression for the redshift-smeared
recombination
emission from the Ly forest
clouds can be obtained through the substitution
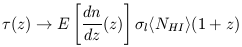
| (8) |
Note that since equation (6) implicitly assumes optically thin
conditions, equations (7)
and (8) are as they stand only valid in that limit. However, the fact
that the redshifted
recombination line emission is bounded by the intensity of the ionizing
input flux is
inherent to the nature of the recombination process and true
regardless of the amount
and detailed spatial distribution of the matter being photoionized and
the recombination
line in question. In other words, since the photoionized intergalactic
gas is simply acting
as a simple photon down-converter, the task of estimating the possible
contribution to
the UV background from line emission from photoionized intergalactic
matter boils
down to the task of estimating the intensity of the ionizing input flux
at high redshift,
IH(z).
The proximity effect displayed by the
Ly forest implies that
IH
10-21 ergs
s-1
cm-2 sr-1 Hz-1 within the 1.7
z
3.8 redshift range that
can be probed with
ground-based telescopes. Judging from Figure 2,
one anticipates an even lower ionizing background of intensity
IH(z)
10-22 ergs
s-1 cm-2 sr-1 Hz-1 at the
redshifts z 1
of interest here. This expectation borne out observationally by recent
observations of
the proximity effect at low redshift carried out with HST
(Kulkarni & Fall 1993)
and by limits on the local extragalactic ionizing flux derived from
H observations of
high-latitude and extragalactic HI clouds
(Reynolds et al. 1986;
Songaila, Bryant & Cowie
1989;
Kutyrev & Reynolds 1989).
This ionizing flux, if redshifted from z
0.5,
corresponds to an equivalent far-UV background of
I
0.4 photons s-1
cm-2 sr-1 Å-1 - an
intensity an order of magnitude below the observational limits on a
possible extragalactic contribution. It follows that redshifted
Ly recombination emission from
the Lyman
forest clouds or a smooth photoionized IGM is not likely to be a
significant contributor to the far-UV background.
A similar conclusion can be reached in the alternative scenario of
Ly emission
from a shock-heated IGM. In the case of collisionally excited emission
from a smooth IGM component, the line emissivity can be written
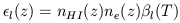
| (9) |
where 
l(T)
is the Ly collisional
excitation rate, and nHI and ne are
the neutral hydrogen
and electron densities in the IGM. The HI density is constrained
observationally by
the Gunn-Peterson limit, equation (3), while the electron density is
constrained by the
total baryonic density of the nearly fully ionized IGM. Combining,
equations (1), (3) and
(9), and introducing ne(z) =
n0e(1 + z)3
where n0e
1.2n0H = 9.3 x 10-6
b
h2 cm-3 is
the present epoch electron density, one obtains the following expression
for the redshift-smeared
Ly background
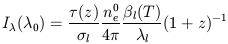
| (10) |
For an ambient IGM temperature of T
105 K as inferred
from considerations of quasar absorption line cloud survival, the
Ly collisional excitation rate
is l
4 x
10-9 cm3 s-1. This value, together with
the Gunn-Peterson limit of (z)
< 0.1, yields
a predicted smeared Ly
intensity of I
4 x 10-2
b
h2 photons s-1 cm-2
sr-1 Å-1
in the far-UV. It follows that collisionally excited
Ly emission from a smooth IGM
component at 0 z
0.7 is a negligible
contributor to the far-UV background for
any reasonable value of b
h2. The reason for this firm conclusion is simply that it
takes intergalactic HI atoms to produce collisionally excited
Ly emission, and
nHI(z)
is severely constrained by the Gunn-Peterson test.
Similar conclusions are reached concerning collisionally excited
emission from the
Lyman forest clouds. The equivalent expression to equation (10) for the
redshift-smeared
Ly background in the clumped
case can be obtained through the substitutions
(8) and ne(z) -> ne. This leads to
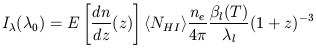
| (11) |
where ne is now the in situ electron density in
the Lyman forest clouds. Based on studies
of correlated Lyman forest absorption in quasar pairs combined with
considerations of reasonable ionization levels
(Carswell 1988;
Sargent 1988),
the gas density in Lyman
forest absorbers is believed to be of order ne
10-3
cm-3. The observed line widths
of the Lyman forest systems limit their temperatures to T
6 x 104 K, in
which case
l
3 x 10-10
cm3 s-1. With these numbers and the values
E[dn / dz(z)] 30 and
< NHI >
1015
cm-2, appropriate to the Lyman forest at z
0.3, equation (11) yields
I
0.3 photons
s-1 cm-2 sr-1
Å-1. Again, we conclude that collisionally excited
Ly emission from the Lyman
forest cannot a significant contributor to the far-UV background.
2.3 Redshifted HeII
304 Å Emission from the
IGM Revisited
As illustrated in Figure 1, the second most
important emission line from a luke warm photoionized or shock-heated
intergalactic primordial plasma is HeII
Ly emission at
304Å. The discussion of
the possible far-UV background contribution due to this source
from very high redshifts (3
z 5) is slightly
more complicated with respect to that
of HI Ly for several
reasons. For one very little is currently known the intergalactic
abundance of the HeII ion, since the HeII
304Å equivalent of the
Gunn-Peterson test
has yet to be carried out in the far-UV with HST or
Lyman/FUSE (cf.
Jakobsen et al. 1993).
The expectation is that if the Lyman forest clouds and an ambient IGM are
indeed photoionized by an
I
-0.5 power law, then the
HeII ion should be an order of
magnitude more abundant than HI, in which case the HeII Gunn-Peterson
effect should
be extremely strong (and HeI absorption very weak). A second important
difference
with respect to HI Ly is that
HeII 304Å emission falls
below the photoionization edge
of neutral hydrogen and is therefore subject to absorption by
intergalactic HI in the
Lyman forest and especially the Lyman limit classes of quasar absorption
systems. This
last topic is addressed in detail in the following section. In spite of
these complications,
it is still possible to draw several reasonably firm conclusions
concerning the possible
contribution of HeII 304Å
emission to the far-UV background.
In the previous section, the intensity of redshifted far-UV
Ly recombination
radiation from photoionized intergalactic gas was constrained on the
basis of estimates on
the metagalactic ionizing background derived from the proximity effect
and more local observations of diffuse
H emission from high-latitude
and extragalactic HI clouds.
The fundamental constraint expressed by equation (7), namely that the
redshifted line
background from a photoionized IGM can never be greater than that of the input
ionizing flux, obviously applies equally well in the case of redshifted
recombination
HeII 304Å emission. In
particular, with a flat
I
-0.5 spectrum for the
metagalactic ionizing background, the intensity of the ionizing flux at
the HeII ionization
edge at 228Å is of the
same order of magnitude as the flux at the Lyman limit at
912Å of
IH(z)
10-21 ergs
s-1 cm-2 sr-1 Hz-1 derived
from the proximity effect
at 1.7 z
3.8. This intensity, if
redshifted from z
4 will give rise to a far-UV
background of intensity
I
1 photons s-1
cm-2 sr-1 Å-1. Since this
background limit
falls far below the observational limits - even without including the
effects of intervening
Lyman continuum absorption - redshifted recombination HeII
304Å emission from
photoionized intergalactic gas can also be ruled out as a significant
source of far-UV background radiation.
Collisionally excited HeII
304Å from a shock-heated
IGM on the other hand is not
quite as easily dismissed. Since the amount of HeII present in
intergalactic space has not
yet been measured by observations of the HeII version of the
Gunn-Peterson test and the
anticipated "helium forest" matching that seen in
Ly, the HeII equivalents of equations
(10) and (11) cannot be used to bracket the possible background
contribution from this
source. Instead, we are forced back to the more theoretical predictions
described by
equation (2). As shown in Figure 1, the net HeII
304Å emissivity per HI
atom peaks
at l
1.2 x 10-12
cm3 s-1 at a temperature T
8 x 104
K. Inserting this maximum
emissivity into equations (1) and (2) yields a predicted far-UV
background intensity at
1600Å of
I
400
2b
h3 photons s-1 cm-2
sr-1 Å-1. Hence depending on the values of
b and
H0, redshifted collisionally excited HeII
304Å radiation from
z 3-5 could in
principle yield a significant far-UV background flux. On the other hand,
considerations
of the survival of quasar absorption line clouds and primordial
nucleosynthesis both
point toward b
0.1, in which case the
HeII line flux is insignificant. In any event, as
discussed in the following section, the census of absorbing HI gas
present in the Universe
represented by the statistics of quasar absorption lines implies that
the far-UV Universe
is opaque in the Lyman continuum out to high redshift. This absorption
will attenuate
any diffuse HeII 304Å
radiation emitted at z
3 by about two orders of
magnitude, thereby reducing even the most optimistic HeII background flux to an
unobservable level.
2.4 Accumulated Lyman Continuum Opacity of the Universe
Any contribution to the far-UV background at observed wavelength
0 emitted
originally at a wavelength below the Lyman limit,
H = 912Å, at
a redshift ze
0 /
H - 1 will be
subject to photoelectric absorption by neutral hydrogen encountered
along at least part of its path. Although it has been known for some
time that the
classical Gunn-Peterson test demonstrates that the Lyman continuum
opacity of any
smoothly distributed IGM is negligible, it has only recently been
fully appreciated that
the statistics of quasar absorption lines imply the that the accumulated
absorption out
to moderate and high redshift from the clumped component is quite substantial.
The character and magnitude of the accumulated Lyman continuum absorption
from the Lyman forest and Lyman limit classes of quasar absorption lines
has been discussed in detail by
Møller & Jakobsen
(1990).
The general expression for the average
transmission through a clumpy medium experienced by a photon emitted at
wavelength,
ze, and received at wavelength,
0, is
(Paresce, Bowyer & McKee
1980)
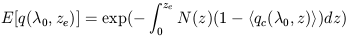
| (12) |
where < qc(0, z) > =
< exp(-NH
H
(0 /
(1 + z))) > is the average individual cloud transmission and
H() is the HI photoelectric cross
section given by
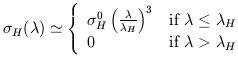
| (13) |
where 0H
= 6.3 x 10-18 cm2 is the photoionization cross
section of neutral hydrogen at the Lyman limit.
As outlined in Section 2.1, the statistics of quasar
absorption systems are today
sufficiently well known to permit a reasonably accurate evaluation of
equation (12).
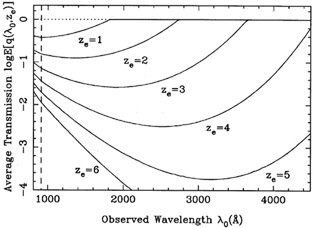
Figure 3 shows, as a function of wavelength, the
resulting accumulated average residual
transmission out to various redshifts from the combined total absorption
due to the
Lyman forest and Lyman limit systems. The characteristic "Lyman valley"
shape of
the accumulated absorption spectrum is caused by the interplay between
the
3
dependence of the HI photoelectric cross section and redshift evolution
and pathlength effects.
The main point to be read from Figure 3 is that
the anticipated net absorption out
to high redshift in the ultraviolet is rather high. As a specific
example, the lower panel
of Figure 4 shows the average residual
absorption at received wavelength
0
1600Å
as a function of emission redshift. From this figure it is seen that any
HeII 304Å
radiation emitted at ze
4.3 will be attenuated by a
factor of order
10-2. This
high opacity effectively implies that even if the IGM did go through a
phase of intense
HeII emission during re-heating, the resulting far-UV background
radiation will in all likelihood remain forever hidden from our view.
It is important to stress that the accumulated intergalactic absorption given in Figures 3 and 4 refers to the average transmission. Since the dominant contributor to the opacity is the scarcer but optically thick Lyman limit systems, large fluctuations
|
Figure 3. Average opacity of the UV universe out to high redshifts as a function of wavelength. The shown "Lyman valley" absorption spectra include the accumulated Lyman continuum opacity from both the Lyman forest and Lyman limit classes of quasar absorption systems. The same absorber parameters as used by Møller & Jakobsen (1990) are assumed. |
around this average are expected along any given line of sight (i.e. in any given quasar spectrum). The magnitude of the fluctuations can be calculated from the expression for the second moment of the accumulated transmission
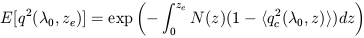
| (14) |
The upper panel of Figure 4 shows the predicted
relative transmission fluctuations,
(
q / q) =
(E[q2] -
E[q]2)1/2 / E[q], as a
function of ze, again for
0 = 1600Å. In the
example of HeII Ly emission
from ze 4.3
quoted above, the 1 level
fluctuations
amount to a factor 5. In
other words, a characteristic signature of any contributor
to the far-UV background originating at high redshift should be an
extremely patchy background component.
|
Figure 4. Lower frame: Average transmission
of the Universe at received wavelength
|
This leads to the interesting prospect of detecting or constraining a
high-z
component to the far-UV background - regardless of its origin - through
measurements of
background intensity fluctuations. In fact, from the observations of
Martin and Bowyer (1989),
it is known that the far-UV background at
0
1600Å is very smooth on
angular scales of 
= 8' and
larger: ( I /
I)
6%. If it is assumed that the
background
consists of the sum of a smooth local component and an attenuated distant high
redshift component of average intensity E[q(z)] Iz,
the fractional contribution to the total
average emission from the distant component,
z, can be estimated from
the observed dilution of the opacity fluctuations
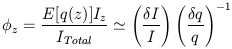
| (15) |
Taken at face value, the
Martin and Bowyer (1989)
fluctuation limit implies that less
than z
6% / 5
1% of the far-UV background
can originate from z
4.3. However,
a slightly subtle point has been overlooked; namely that the
( q / q) values in
Figure 4
refer statistically to the absorption sampled along an infinitely narrow
pencil beam
(namely the line of sight to a quasar), whereas the UV background
observations have
been obtained with a finite
= 8' beam size. Since the opacity is dominated by the
Lyman limit absorbers, which are assumed to be associated with galaxy
halos of, say,
D 50 kpc size, the
absorption-generated background fluctuations on the sky are
expected to be correlated only on very small scales of order
c
cD / H0
10". Such
small scale fluctuations would only appear in the finite beam
measurements of
Martin and Bowyer (1989)
diluted by a factor of order
/ c
50. The upper limit on
z
derived above therefore has to be relaxed by the same amount to
z
50%. Given
the severe practical problems of measuring UV background fluctuations on
such small
scales as
10", it is unlikely that
this constraint will be tightened much further in the
foreseeable future. On the other hand, the above considerations do serve
to demonstrate
that, because of the very small size of the anticipated absorption
coherence patch on
the sky, use of the average attenuation given by equation (12) is well
justified when
dealing with the radiative transfer of diffuse background light.
1 Throughout this paper
I refers to
the specific intensity of the background expressed
in the units preferred by the observers; namely photons s-1
cm-2 sr-1 Å-1.
Back.