Copyright © 1981 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1981. 19:
373-410 Copyright © 1981 by Annual Reviews. All rights reserved |
We assume throughout that the radio emission is due to partially
opaque electron synchrotron radiation. For a uniform source of angular
size,  , a red shift, z,
magnetic field, B, and for a power-law
distribution of particle energy given by N(E) dE
, a red shift, z,
magnetic field, B, and for a power-law
distribution of particle energy given by N(E) dE
 E
E dE, the
frequency,
dE, the
frequency,  m, where the
flux density reaches a maximum value, Sm,
(
m, where the
flux density reaches a maximum value, Sm,
( ~ 1) is given approximately
by (2)
~ 1) is given approximately
by (2)
The function
f(
Variations in opacity throughout the source lead to an overall
spectrum that can be considered as the superposition of many simple
regions described by Equation (1) and can give rise to the so-called
flat or undulating spectra typically observed over a wide range of
frequency.
Synchrotron radiation losses lead to a characteristic electron
half-life at
In very compact sources, in which the radiation energy density is
comparable to the magnetic energy density, inverse Compton scattering
causes additional electron energy losses, which lead to an upper limit
to the observable brightness temperatures of ~ 1012 K
(Kellermann &
Pauliny-Toth 1969).
In principle, the magnetic field, B, and energy
content in the form of relativistic particles, Ep, and
magnetic
fields, Em, may be estimated from detailed observation of the
brightness distribution at many wavelengths which give the
distribution of opacity and brightness temperature. Because the
calculated values of B, Ep, and
Em depend on the observables
2
Throughout this paper values of flux densities, S, are given in Jy;
angular sizes, 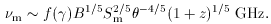
 ) only
weakly depends on
) only
weakly depends on  , and for
, and for  = 2, f(
= 2, f( ) ~ 8.
At frequencies
) ~ 8.
At frequencies  >>
>>
 m, the spectrum is given
by the usual power law S
m, the spectrum is given
by the usual power law S


 , where the spectral index,
, where the spectral index,
 = (1 -
= (1 -
 ) / 2. At
frequencies
) / 2. At
frequencies  <<
<<
 m,
S
m,
S 

 with
with
 = 2.5, a value characteristic
of a homogeneous opaque synchrotron source.
= 2.5, a value characteristic
of a homogeneous opaque synchrotron source.
 m of
m of
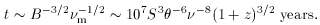
 and
and
 m,
raised to a power ~ 10, accurate determinations are not feasible with
the limited data currently available. Rough estimates indicate B ~
10-3±1 gauss, Ep ~
105.2-5.6 ergs, and Em some 10 orders of
magnitude
less. Detailed formulae for calculating B, Ep,
and Em from the
observables
m,
raised to a power ~ 10, accurate determinations are not feasible with
the limited data currently available. Rough estimates indicate B ~
10-3±1 gauss, Ep ~
105.2-5.6 ergs, and Em some 10 orders of
magnitude
less. Detailed formulae for calculating B, Ep,
and Em from the
observables  ,
,
 m, and
Sm including the effect of complex geometries are given by
Pacholczyk (1970),
Jones et al. (1974),
and Moffet (1975).
m, and
Sm including the effect of complex geometries are given by
Pacholczyk (1970),
Jones et al. (1974),
and Moffet (1975).
 , in milliarcsec
= mas; magnetic fields, B, in gauss,
and frequencies,
, in milliarcsec
= mas; magnetic fields, B, in gauss,
and frequencies,  , in GHz. For
calculations involving distance, we
take H = 50 km s-1 Mpc-1 and
q0 = 0. Back.
, in GHz. For
calculations involving distance, we
take H = 50 km s-1 Mpc-1 and
q0 = 0. Back.