Copyright © 1981 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1981. 19:
373-410 Copyright © 1981 by Annual Reviews. All rights reserved |
3.1 Effect of Opacity
It is generally assumed that in the compact radio sources the observed flat spectra are due to synchrotron self-absorption, although this is sometimes challenged because of the lack of observed sharp spectral cutoffs and the absence of any spectra with an index as steep as +2.5, the value expected from a completely opaque synchrotron source. We do not, however, consider this a serious objection to the general class of opaque synchrotron models since, as in the case of thermal sources, the form of the observed spectra can be at least qualitatively interpreted in terms of spatial inhomogeneities, which cause different parts of the source to become opaque at different wavelengths and thus broaden the self-absorption cutoff, or lead to several minor "peaks" or "valleys." The shape of the observed spectra, as well as the VLBI observations discussed in Section 5, suggest that the compact sources contain a small number of distinct components with well-defined cutoff frequencies. It is, however, difficult to understand, in that case, the apparently fortuitous circumstances which cause the different components to add together in just the way required to produce the remarkably flat spectra that are sometimes observed over a wide range of frequencies (Cook & Spangler 1980). Nevertheless, VLBI observations of 0735 + 17 (Cotton et al. 1980, Marscher & Shaffer 1980, and Bååth et al. 1981), a source with a very smooth flat spectrum, do indeed confirm that it is composed of a number of discrete components, a fact to which Cotton et al. refer as a "Cosmic Conspiracy."
Condon & Dressel (1973), de Bruyn (1976), and Marscher (1977a) have suggested that the flat spectra may be interpreted in terms of a radial distribution of magnetic field strength and particle energy density of the form
where m = 1 and n = 2.
Spangler (1980)
has also interpreted a variety of spectra observed by
Owen et al. (1980)
in terms of inhomogeneous
synchrotron models with somewhat different values of m and
n. According to these models, the radiation observed at the longer
wavelengths comes from a larger region, and the effective source
dimensions are expected increase approximately linearly with
wavelength. For a typical brightness temperature of 5 x 1011 K, the
characteristic source dimensions of radiating region are given by
Although the VLBI observations tend to support models that consist of
multiple inhomogeneous components with brightness temperatures in the
range 1011 to 1012 K
(Kellermann 1978,
Marscher & Shaffer
1980),
they must be viewed with some caution owing to the bias introduced by using
fixed-length interferometers whose resolution also varies directly with
frequency.
Jones & Hardee (1979) and
Spangler (1980)
have considered
transparent models with a Maxwellian rather than conventional
power-law energy distribution, and find good agreement with some of
the observed spectra. Uniformly flat spectra can also be represented
by optically thin synchrotron models with a relatively flat electron
energy distribution (i.e.
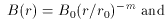
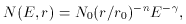
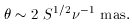
 ~ 1), although
such models appear to
require higher infrared and optical flux densities than are observed
(Marscher 1977b).
Moreover, high brightness temperatures that are
deduced from the VLBI observations, the sharp spectral cutoffs that
are sometimes observed, the peaks and valleys often seen in the
overall spectra, and the spectra of individual components determined
from multi-frequency VLBI observations, suggest that the effects of
opacity are more important than the form of the electron energy
distribution in determining the spectra of compact radio sources, at
least at centimeter wavelengths. At millimeter wavelengths, on the
other hand, the spectra often follow a power law with an index ~
-0.25, corresponding to an optically thin synchrotron source and a
power-law electron energy distribution with an index,
~ 1), although
such models appear to
require higher infrared and optical flux densities than are observed
(Marscher 1977b).
Moreover, high brightness temperatures that are
deduced from the VLBI observations, the sharp spectral cutoffs that
are sometimes observed, the peaks and valleys often seen in the
overall spectra, and the spectra of individual components determined
from multi-frequency VLBI observations, suggest that the effects of
opacity are more important than the form of the electron energy
distribution in determining the spectra of compact radio sources, at
least at centimeter wavelengths. At millimeter wavelengths, on the
other hand, the spectra often follow a power law with an index ~
-0.25, corresponding to an optically thin synchrotron source and a
power-law electron energy distribution with an index,
 ~ 1.5. Thus
N(E) = KE-1.5 appears to describe the electron
energy distribution, and
models of acceleration mechanisms must account for this.
~ 1.5. Thus
N(E) = KE-1.5 appears to describe the electron
energy distribution, and
models of acceleration mechanisms must account for this.