


The universe is not exactly homogeneous and isotropic, but it is a sufficiently accurate description of the universe on large scales that it is useful to consider homogeneity and isotropy as a first approximation, and discuss departures from this idealized smooth universe.
Let us begin by considering the density field,  (
(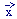 ). If the
average density of the universe is denoted as <
). If the
average density of the universe is denoted as <  >, then we can
define a dimensionless density contrast
>, then we can
define a dimensionless density contrast  (
(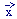 ) as
) as
Of course we cannot predict
where V is some irrelevant normalization volume. After a little
Fourier manipulation and some mild assumptions about the density
field, it is easy to show that the two-point autocorrelation function
of the density field can be expressed solely in terms of
|
where A is yet another irrelevant constant.
So long as the fluctuations are Gaussian, all statistical information
is contained in a quantity known as the power spectrum, which
can be defined as either
The first choice is much more physical, as it represents the power per
logarithmic decade in the fluctuations. Although the first choice
makes much more sense, the second choice is what is usually used. It
turns out that graphs of P (k) have a nicer form (but less physical
content) than corresponding graphs of 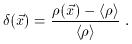
 (
(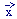 ), but we can hope to
predict the statistical properties of
), but we can hope to
predict the statistical properties of  (
(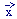 ). The correct
arena to discuss the statistical properties of the density field is in
Fourier space, where one decomposes the density contrast into its
various Fourier modes
). The correct
arena to discuss the statistical properties of the density field is in
Fourier space, where one decomposes the density contrast into its
various Fourier modes  (
(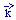 ):
):
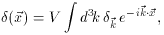
 (
(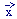 ) |2:
) |2:
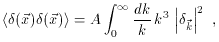
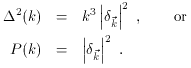
 2 (k). Since the
widespread availability of color graphics, presentation seems to be
everything, and information content of secondary concern.
2 (k). Since the
widespread availability of color graphics, presentation seems to be
everything, and information content of secondary concern.