


2.2 The Power Spectrum Deduced From the Cosmic Background Radiation
The microwave background is isotropic to about one part in 103. If one removes the anisotropy caused by our motion with respect to the cosmic background radiation (CBR) rest frame, then it is isotropic to about 30 parts-per-million. But as first discovered by the Cosmic Background Explorer (COBE), there are intrinsic fluctuation in the temperature of the CBR.
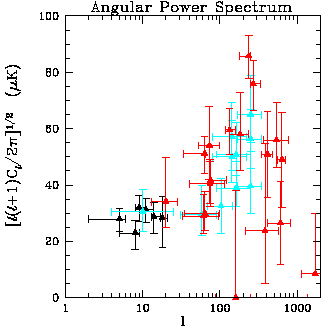
|
| Figure 2. The angular power spectrum of CBR fluctuations (courtesy of Dick Bond and Llyod Knox). |
Just as perturbations in the density field were expanded in terms of
Fourier components, a similar expansion is useful for temperature
fluctuations. Because the surface of observation about us
can be described in terms of spherical angles  and
and  ,
the correct expansion basis is spherical harmonics,
Ylm (
,
the correct expansion basis is spherical harmonics,
Ylm ( ,
,  ). If the average temperature is
< T >, then one can expand
). If the average temperature is
< T >, then one can expand
Of course < alm > = 0, but with proper averaging,
Cl as a function of l is called the angular
power spectrum. In
the six years since the first measurement of CBR fluctuations by COBE,
a number of experiments have detected
fluctuations. The present situation is illustrated in
Fig. 2.
Associated with a multipole number l is a characteristic angle
Contributing to the temperature anisotropies are fluctuations in the
gravitational potential on the surface of last scattering. Photons
escaping from regions of high density will suffer a larger than
average gravitational redshift, hence will appear to originate from a
cold region. In similar fashion, photons coming to us from a
low-density region will appear hot. In this manner, temperature
fluctuations can probe the density field on the surface of last
scattering and provide information about the power spectrum on scales
much larger than can be probed by conventional large-scale structure
observations.
The region of wavenumber and amplitude of the power spectrum probed by
COBE is illustrated in Fig. 3. There are now
measurements of CBR fluctuations on smaller angular scale,
corresponding to larger k.
Finally, Fig. 4 combines information from both
large-scale structure surveys and CBR temperature fluctuations. The
trend is obvious: on small distance scales the power spectrum is
``large,'' which implies a lot of structure. Matter is clustered on
small scales. But on ``large'' scales the power spectrum decreases.
As one examines the universe on larger scales, homogeneity and
isotropy becomes a better and better approximation.
The data shown is only illustrative of many data sets. Although
combining different data sets is uncertain and risky (problems with
normalization, etc.) the qualitative features are the same.
Figure 4 is best regarded as an impressionist
representation of the situation.
Another thing to keep in mind is that the power spectrum may not be
the entire story. The power spectrum contains all statistical
information about the perturbations only if the fluctuations are
Gaussian. This should be cause for concern, because even if the
initial perturbations are Gaussian, eventually they will become
non-Gaussian once the perturbations become nonlinear. Also, the power
spectrum is not a useful discriminant for prominent features such as
walls, voids, filaments, etc. In spite of its drawbacks, the power
spectrum is remarkably useful - if we can't get the power spectrum
right, then we are not on the right track.
Now we turn to an early-universe theory that can account for the power
spectrum: inflation
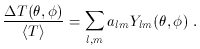
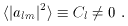
 , and a length scale we can
define as the distance subtended
by
, and a length scale we can
define as the distance subtended
by  on the surface of last
scattering. Since the distance to
the last scattering surface of the microwave background is so large,
the temperature fluctuations represent the largest structures ever
seen in the universe.
on the surface of last
scattering. Since the distance to
the last scattering surface of the microwave background is so large,
the temperature fluctuations represent the largest structures ever
seen in the universe.
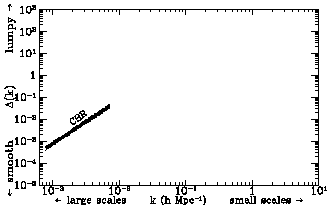
Figure 3. The power spectrum deduced by
measurements of large angular scale CBR temperature fluctuations.
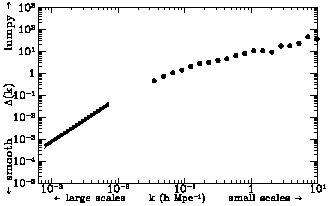
Figure 4. The ``grand unified'' power spectrum, including
determinations from large-scale structure surveys (the points), and
deduced from CBR temperature fluctuations (the box).