


The qualitative discussion of the previous section can be turned into a quantitative estimate for MBH as follows. The quasar population produces an integrated comoving energy density of
where
In fact, the brightest quasars must have had much higher masses. A BH
cannot accrete arbitrarily large amounts of mass to produce arbitrarily high
luminosities. For a given MBH, there is a maximum
accretion rate above
which the radiation pressure from the resulting high luminosity blows away the
accreting matter. This ``Eddington limit'' is discussed in the preceeding
article. Eddington luminosities of L ~ 1047 erg
s-1 ~ 1014
L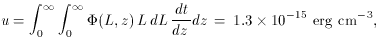
 (L, z) is the comoving
density of quasars of luminosity L at
redshift z and t is cosmic time. For a radiative energy
conversion efficiency of
(L, z) is the comoving
density of quasars of luminosity L at
redshift z and t is cosmic time. For a radiative energy
conversion efficiency of
 , the equivalent
present-day mass density is
, the equivalent
present-day mass density is
 u =
u / (
u =
u / ( c2) = 2.2 x
104
c2) = 2.2 x
104  -1
M
-1
M Mpc-3.
Comparison of
Mpc-3.
Comparison of  u with the overall galaxy luminosity density,
u with the overall galaxy luminosity density,
 g
g
 1.4 x 108 h
L
1.4 x 108 h
L Mpc-3, where the Hubble constant is
H0 = 100 h km s-1 Mpc-1,
implies that a typical nearby bright
galaxy (luminosity L*
Mpc-3, where the Hubble constant is
H0 = 100 h km s-1 Mpc-1,
implies that a typical nearby bright
galaxy (luminosity L*  1010 h-2
L
1010 h-2
L ) should
contain a dead quasar of mass MBH ~ 1.6 x 106
) should
contain a dead quasar of mass MBH ~ 1.6 x 106
 -1
h-3
M
-1
h-3
M .
Accretion onto a BH is expected to produce energy with an efficiency of
.
Accretion onto a BH is expected to produce energy with an efficiency of
 ~ 0.1, and the best
estimate of h is 0.71 ± 0.06. Therefore
the typical BH should have a mass of ~ 107.7
M
~ 0.1, and the best
estimate of h is 0.71 ± 0.06. Therefore
the typical BH should have a mass of ~ 107.7
M . BHs in dwarf
ellipticals should have masses of ~ 106
M
. BHs in dwarf
ellipticals should have masses of ~ 106
M .
.
 require BHs
of mass MBH
require BHs
of mass MBH
 109
M
109
M . These
arguments define the parameter range of interest: MBH
~ 106 to 109.5
M
. These
arguments define the parameter range of interest: MBH
~ 106 to 109.5
M . The
highest-mass BHs are likely to be rare, but low-mass
objects should be ubiquitous. Are they?
. The
highest-mass BHs are likely to be rare, but low-mass
objects should be ubiquitous. Are they?