At times significantly before decoupling, the universe is hot enough that protons and electrons exist freely in a plasma. During this epoch, the rate for photons to Thomson scatter off of free electrons is large compared to the expansion rate of the universe. Thus, the photons and electrons stay in thermal equilibrium at a common temperature and are said to be tightly coupled. As the universe drops below a temperature of around 0.1 eV at a redshift of around 1300, the electrons and protons begin to ``recombine'' into neutral hydrogen. Within a short time, almost all the free electrons are converted to neutral hydrogen, the rapid Thomson scattering ceases for lack of scatterers, and the radiation is said to decouple. At this point, the radiation will propogate freely until the universe reionizes at some redshift greater than 5.
During the tight coupling epoch, the photons must have a distribution which mirrors that of the electrons. An immediate consequence is that the angular dependence of the radiation field at a given point can only possess a monopole (corresponding to the temperature) and a dipole (corresponding to a Doppler shift from a peculiar velocity) component, and that the radiation field is unpolarized. Any higher multipole moment will rapidly damp away as the electrons scatter off the free electrons, and no net polarization can be produced through scattering.
A quadrupole is subsequently produced at decoupling
as free streaming of the photons begins. A single Fourier mode of the
radiation field can be described by the temperature distribution
function 
(k,
µ, 
)
where k is the wavenumber,
µ =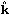 
. 
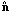is the angle
between the
vector k and the propagation direction
,
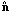and is conformal
time. (For mathematical simplicity only a flat
universe is considered here, although the non-flat cases are
no more complicated conceptually.) Ignoring
gravitational potential contributions, free streaming of the photons
is described by the Liouville equation
+
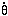ikµ = 0. If
the free streaming begins at time
*,
then the solution at a later time is simply
(k, µ,
) =
(k, µ,
*)
exp(-ikµ(
- *)).
We can reexpress the µ dependence as a multipole expansion
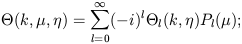
| (21) |
using the identity
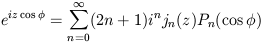
| (22) |
the free streaming becomes
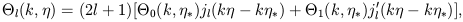
| (23) |
where jl is the usual spherical Bessel function.
We are interested in the behavior of the free streaming
at times near decoupling; at later times, the number density of
free electrons which can Thomson scatter has dropped to negligible
levels and no further polarization can be produced. The physical
length scales of interest for microwave background fluctuations
will be larger than the thickness of the last scattering surface,
so k( -
*)
will be small compared to unity. For small
arguments x << 1, jl(x) /
jl'(x) ~ x / l,
which implies that if the monopole
and dipole radiation components are initially of comparable size,
free streaming through the region of polarization generation
with thickness 
will generate
a quadrupole component from the dipole which is a factor of
2 / (k )
larger than the quadrupole component from the monopole. In other
words, on length scales large compared to the thickness of
the surface of last scattering, the quadrupole moment and thus
the polarization couples much more strongly to the velocity
of the baryon-photon fluid than to the density.
Note that on smaller scales with
k
1, the polarization
can couple more strongly to either the velocity or the density,
depending on the scale, but for standard recombination
these scales are always small enough
that the microwave background fluctuations are strongly
diffusion damped.