Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
613-52 Copyright © 1992 by Annual Reviews. All rights reserved |
Redshifts are the key measurement required to translate observable magnitudes, colors, and angles into physical luminosities, rest-frame spectral energy distributions, intrinsic sizes and projected separation distances. Depending on the spectral resolution and signal-to-noise ratio, the spectra used for redshifts may also yield a wealth of additional information on the physical conditions of line-emitting hot gas; limits to the age and metallicity of the component stellar populations; and a measure of mass from velocity widths of spectral features.
The pioneering effort in measuring redshifts of field galaxies faint enough to probe galaxy evolution (B ~ 20) was by E. Turner, J. Gunn, and W. Sargent in the late 1970's using the Palomar 5-m telescope and the SIT digital spectrograph. Their sample was selected visually by R. Kron to span a wide range in morphology and surface brightness. Their results were briefly described by Turner (1980) and Gunn (1982), and they generously allowed 58 redshifts to be published by Koo (1985). Since then, a number of fainter, better-defined redshift surveys of field galaxies have been undertaken as detailed in Section 2.4.2.
2.4.1 REDSHIFT SURVEYS 15 < B < 17
2.4.2 REDSHIFT SURVEYS B > 17
Several groups have attempted redshift surveys with
hopes of pushing beyond B = 20 to z > 0.2 where evolution
might be detectable. Most well known (and fully published)
are the surveys of
Broadhurst, Ellis, and
Shanks (1988) of
187 galaxy redshifts to B = 21.7, and
Colless et al. (1990)
of 87 galaxies to B = 22.5. The former group used a multiple
optical-fiber system, while the latter group used a mask with
multiple slits and a wide-field spectrograph camera. Both
surveys are roughly 80% complete.
Lilly, Cowie, and
Gardner (1991)
reported six spectroscopic redshifts to B ~ 24, and
Cowie, Songaila, and
Hu (1991)
have extended this survey to
obtain an almost complete sample of 21 redshifts to the same
limit. The largest survey is that undertaken at Kitt Peak
National Observatory by
Koo and Kron (1987)
with over 400
redshifts complete for B < 20, but less than 50% complete at
B ~ 22. This sample has yet to be published in detail, but
some of the data will be presented for illustration. The
Broadhurst, Ellis, and Shanks sample has only blue
magnitudes; the Colless et al. sample has B - R colors as well;
the Koo and Kron surveys have
UbJrFI photographic photometry;
the Lilly, Cowie, and Gardner survey has UBVI CCD photometry;
and the Cowie, Songaila, and Hu sample has in addition very
deep K-band photometry.
Figure 3 gives the bJ -
rF colors versus redshift for a
subsample of faint galaxies with redshifts and measured
colors that can be reliably transformed to our system. The
expected red and blue boundaries have been derived from
redshifting appropriate empirical spectra through the bJ and
rF passbands (these spectra are well matched by the model
spectral energy distributions discussed in
Section 3.3). In
general the data do fall within the expected boundaries, but
it is noteworthy that, if the colors are accurate, galaxies
even bluer than NGC 4449 are present at all redshifts (see also
Colless et al. 1990).
Moreover, field galaxies at
z > 0.5 can be found which appear similar to local elliptical
galaxies, a result consistent with the findings of
Oke (1983)
and Hamilton (1985),
who used the continuum break at 4000 Å instead of colors.
Figure 4 shows the data in the form of redshift versus
blue magnitude (the points from
Dressler and Gunn 1992
are discussed in Section 2.5). Horizontal bands
of points within a given survey reflect large-scale structure along the line
of sight. Such structures can be seen in the authors' data
at intermediate magnitudes, 18 < B < 20, even though five
separate fields have been combined in this plot. It is
evident from the distribution of points in
Figure 4 that the
average underlying redshift distribution cannot be accurately
derived from samples of even hundreds of galaxies at large
distances. The diagonal lines indicate approximate loci of
constant luminosity (more accurately, the K-correction and
cosmological factors make the corresponding apparent
magnitudes fainter at a given redshift). It can also be seen
that galaxies of quite low luminosity, i.e. true dwarf
galaxies, appear at all magnitudes, but in relatively small
numbers (cf.
Cowie et al. 1992;
Cowie, Songaila, and
Hu 1991).
If field galaxies were overall more luminous at earlier
epochs, one would expect the distribution of points in
Figure 4 to be shifted progressively to brighter
apparent magnitudes
at higher redshifts. The early-type galaxies might have been
brighter by approximately 0.5 mag at z = 0.5
(Tinsley 1972),
roughly comparable (but of opposite sign) to the
K-correction. The luminosity evolution of the later-type
galaxies depends on the unknown change in the rate of star
formation and may well have been less strong. One might
conservatively expect that evolution in
Figure 4 would be a
subtle effect, especially considering the modulation of the
data by the large-scale structure.
Figure 5 gives the cumulative redshift
distributions for these same surveys, binned in apparent magnitudes as
described in the caption. The normalized cumulative redshift
distributions are useful in principle because even incomplete
samples can be used, so long as the incompleteness is
unbiased in redshift. Unfortunately, this qualification is
expected to be difficult to achieve in practice for B > 21,
and thus one should be cautious in accepting the B > 21
samples in Figure 5 as being representative. A
priori we expect a smooth dependence on magnitude of the separate
cumulative redshift distributions. Luminosity evolution may
manifest itself as a relatively subtle change in the shape of
the high-redshift tails, and the change should be smoothly
progressive between intervals of apparent magnitude. On this
basis, it seems likely that the faintest bin, B > 23, is
incomplete at high redshifts.
Broadhurst, Ellis, and
Shanks (1988) have argued that
since the median redshift matches their no-evolution model
while the observed counts are too steep, evolution in the
shape of the luminosity function is required, a conclusion
that was echoed by
Colless et al. (1990).
Galaxies that are currently of lower luminosity may have experienced more
frequent bursts of star formation at the relevant redshifts,
z > 0.1. This argument was supported by co-adding in the
rest-frame the spectra of six galaxies with relatively strong
W3727. The mean spectrum showed strong Balmer lines in
absorption and a blue continuum, indicative of an episode of
recent star formation. This is a promising technique, and
with additional data it will be possible to look for
correlations of Balmer absorption-line strength with absolute
magnitude and with redshift.
The evolutionary picture of
Broadhurst, Ellis, and
Shanks (1988)
and Colless et
al. (1990)
is however not unique, as
Guiderdoni and
Rocca-Volmerange (1990)
have been able to account for the data without such luminosity-
dependent luminosity evolution. We shall return to the
interpretation of the redshift distributions later, but
stress a number of cautionary points for accepting these
faint redshift surveys as necessarily being representative.
Of most importance is the completeness, especially for higher
redshift galaxies, since these are expected from surface
brightness considerations (Section 1) to be the most
difficult to measure at a given magnitude. Unless surveys
achieve close to 100% completeness, the missing galaxies are
most likely to be exactly those of most interest for tests of
evolution or cosmology. Thus far, not a single galaxy with z
> 1 has been spectroscopically measured with high reliability
in the above surveys (but see next section on samples
selected in other ways). Unless this failure is due to a
true lack of such galaxies in the samples, it may only
reflect the unfortunate circumstance that at high redshifts,
strong spectral features like the 4000 Å continuum break move
into the very noisy red portion of the sky. For emission-line galaxies,
only the [OII] 3727 doublet is visible at
redshifts z ~ 0.5 when the redder set of confirming emission
lines, H
Independent samples can, however, be compared over
similar magnitude ranges to check the completeness and to
examine the distribution of the high redshift tail. It is
possible that there has indeed been a systematic loss of high
redshifts among the
Broadhurst et
al. (1988) and
Colless et al. (1990)
samples. The fainter portion of the
Broadhurst, Ellis, and
Shanks (1988)
sample is relatively less complete
but happens to overlap the bright and virtually complete
portion of the
Colless et al. (1990)
sample between bJ = 21
and 21.7. Using the Kolmogorov-Smirnov test, we find, in
this overlapping magnitude range, less than a 1% chance that
the two distributions were drawn from the same parent
population, with the more complete Colless et al. sample
showing a more extended high-redshift tail (23% with z > 0.4,
versus 4% for the less complete Broadhurst, Ellis, and Shanks
sample).
As for the
Colless et al. (1990)
sample, one would
expect a larger number of dimmer or weaker-emission-lined
galaxies at z > 0.6 than are observed. Their incompleteness
has recently been decreased from 19% to 5%, yet this paucity
of high-redshift galaxies persists (Ellis, private
communication). However, the galaxies selected for the
redshift survey show an apparent deficit at the faint end,
22.2 < B < 22.5, of about a factor of two with respect to the
expected count distribution. Another problem pointed out by
Colless et al. (1990)
is that one of their three fields has a
higher redshift tail and appears to be inconsistent with the
other two fields, which was attributed to clustering.
Moreover, for a sample of only eight galaxies in the same
magnitude range, B = 21 to 22.5,
Cowie, Songaila, and
Hu (1991)
find one at z = 0.735 (with broad emission lines
indicative of a Seyfert-like spectrum), another at z = 0.644,
and one at z = 0.479. The published sample of
Colless et al. (1990)
is 11 times larger, but has only two galaxies with
z > 0.6, and only 15 galaxies with z > 0.45. The various
strong selection effects mentioned earlier must be better
understood, and the surveys must reach a greater level of
self-consistency, before more conventional expectations for
the galaxy redshift distribution can be rejected with
confidence.
Apart from the issues of incompleteness just discussed,
the distribution of redshifts within an interval of apparent
magnitude, and in particular the median redshift, is a more
problematic test for evolution than it might first seem. The
low end of the redshift distribution at a fixed apparent
magnitude contains information only about the faint end of
the luminosity function, and is particularly susceptible to
the effects of large-scale structure because the volume
sampled is small. On the other hand, the high-redshift end
of the distribution contains information not only about the
bright end of the luminosity function, but also about the
volume element, the overall effective K-correction, and
galaxy evolution. Tests for evolution should weight high
redshifts more than low redshifts, because the unweighted
median may be affected by irrelevant uncertainties at low
redshift.
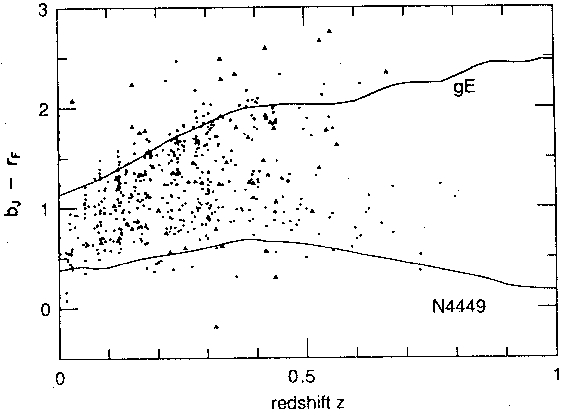
Figure 3. bJ - rF color of
galaxies versus their spectroscopic redshifts. The dots are the authors'
data; the triangles are from
Colless et al. (1990),
transformed in color according to
Metcalfe et al. (1991).
The curves show the colors of an average elliptical galaxy (gE) and
NGC 4449 (Bruzual, private communication).
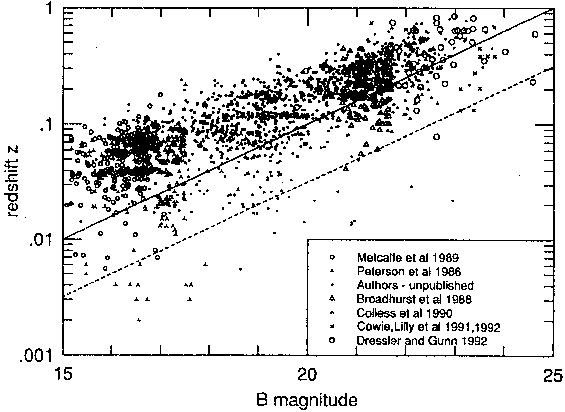
Figure 4. Log redshift versus blue magnitude of major
redshift samples with magnitude limits fainter than B = 16.
Completeness, reliability, and selection effects vary and
have not been made homogeneous. The
Dressler & Gunn (1992)
sample consists of their interlopers, i.e. foreground and
background galaxies in their rich cluster fields. The
diagonal lines indicate simply the inverse-square law,
B = 5 log z + 25 for the solid line, corresponding roughly to
0.1 L* (the dashed line is drawn for 0.01 L* to indicate the
luminosities of true dwarfs). The lines correspond to q0 = 1
and zero effective K-correction. For a smaller value of
q0
and a K-correction that applies to an average of non-evolving
field galaxies, at high redshift the lines bend away from the
naive inverse-square law towards fainter magnitudes, like the
upper envelope of the distribution of data points.
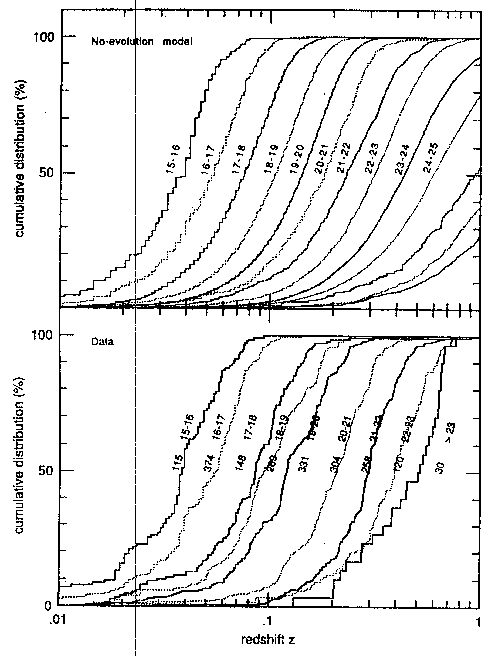
Figure 5. Cumulative distribution functions versus redshift
for samples binned in steps of one magnitude. The top panel
gives the homogeneous no-evolution model discussed in the
text, and the bottom panel is derived from
Figure 4 as follows. The number of galaxies
contributing to each magnitude bin is indicated. The leftmost curve is for
B = 15-16 (thicker solid line), the next B = 16-17
(thinner dotted line), and so on as indicated. The brightest two bins
were derived from
Peterson et
al. (1986) and
Metcalfe et al. (1989);
the next three bins, to B = 20, are from the authors;
the following bin (B = 20-21) includes both the
Broadhurst et al. (1988)
sample and that of the authors; B = 21-22 includes
those two samples and that of
Colless et al. (1990);
B = 22-23 and B > 23 are from
Colless et
al. (1990), authors,
Cowie, Songaila, and
Hu (1991), and
Dressler and Gunn (1992).
 and [OIII]
5007, move into the red.
and [OIII]
5007, move into the red.