2.4 The Chi-Square Distribution
As we will see in Section 7, the chi-square
distribution is
particularly useful for testing the goodness-of-fit of theoretical
formulae to experimental data. Mathematically, the chi-square is
defined in the following manner. Suppose we have a set of n
independent random variables, xi, distributed as
Gaussian densities
with theoretical means µi and standard
deviations 
i,
respectively. The sum
is then known as the chi-square. This is more often designated by the
Greek letter
where v is an integer and
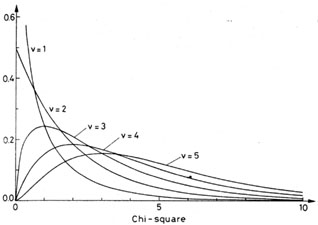
Fig. 6. The chi-square distribution for
various values of the degree of freedom parameter v.
Figure 6 plots the chi-square distribution for
various values of
v. The mean and variance of (23) can also be shown to be
To see what the chi-square represents, let us examine (22) more
closely. Ignoring the exponent for a moment, each term in the sum is
just the deviation of xi from its theoretical mean
divided by its
expected dispersion. The chi-square thus characterizes the
fluctuations in the data xi. If indeed the
xi are distributed as
Gaussians with the parameters indicated, then on the average, each
ratio should be about 1 and the chi-square, u = v. For any
given set
of xi, of course, there will be a fluctuation of
u from this mean with
a probability given by (23). The utility of this distribution is
that it can be used to test hypotheses. By forming the chi-square
between measured data and an assumed theoretical mean, a measure of
the reasonableness of the fluctuations in the measured data about this
hypothetical mean can be obtained. If an improbable chi-square value
is obtained, one must then begin questioning the theoretical
parameters used.
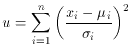
2; however, to avoid confusion due to the
exponent we
will use u = 2 instead. Since xi is a
random variable, u is also a
random variable and it can be shown to follow the distribution
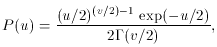
(v / 2) is the gamma
function. The integer v
is known as the degrees of freedom and is the sole parameter of the
distribution. Its value thus determines the form of the distribution.
The degrees of freedom can be interpreted as a parameter related to
the number of independent variables in the sum (22).
