


4.2 The Maximum Likelihood Method
The method of maximum likelihood is only applicable if the form of the
theoretical distribution from which the sample is taken is known. For
most measurements in physics, this is either the Gaussian or Poisson
distribution. But, to be more general, suppose we have a sample of n
independent observations x1, x2,
. . . ,xn, from a theoretical
distribution f(x |  )
where
)
where  is the parameter to be
estimated. The method then consists of calculating the likelihood
function,
is the parameter to be
estimated. The method then consists of calculating the likelihood
function,
which can be recognized as the probability for observing the sequence
of values x1, x2, . . .,
xn. The principle now states that this
probability is a maximum for the observed values. Thus, the parameter
If there is more than one parameter, then the partial derivatives of L
with respect to each parameter must be taken to obtain a system of
equations. Depending on the form of L, it may also be easier to
maximize the logarithm of L rather than L itself. Solving
the equation
then yields results equivalent to (30). The solution,
It should be realized now that
This is a general formula, but, unfortunately, only in a few simple
cases can an analytic result be obtained. An easier, but only
approximate method which works in the limit of large numbers, is to
calculate the inverse second derivative of the log-likelihood function
evaluated at the maximum,
If there is more than one parameter, the matrix of the second
derivatives must be formed, i.e.,
The diagonal elements of the inverse matrix then give the approximate
variances,
A technical point which must be noted is that we have assumed that
the mean value of
Another useful property of maximum likelihood estimators is
invariance under transformations. If u =
f(
Let us illustrate the method now by applying it to the Poisson and
Gaussian distributions.
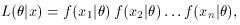
 must be such that L is a
maximum. If L is a regular function,
must be such that L is a
maximum. If L is a regular function,
 can
be found by solving the equation,
can
be found by solving the equation,
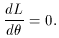
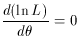
 , is known as
the maximum likelihood estimator for the parameter
, is known as
the maximum likelihood estimator for the parameter
 . In order to
distinguish the estimated value from the true value, we have used a
caret over the parameter to signify it as the estimator.
. In order to
distinguish the estimated value from the true value, we have used a
caret over the parameter to signify it as the estimator.
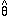 is also a random
variable, since it
is a function of the xi. If a second sample is taken,
is also a random
variable, since it
is a function of the xi. If a second sample is taken,
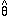 will have a
different value and so on. The estimator is thus also described by a
probability distribution. This leads us to the second half of the
estimation problem: What is the error on
will have a
different value and so on. The estimator is thus also described by a
probability distribution. This leads us to the second half of the
estimation problem: What is the error on
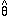 ? This is given by the
standard deviation of the estimator distribution We can calculate this
from the likelihood function if we recall that L is just the
probability for observing the sampled values x1,
x2,. . ., xn. Since
these values are used to calculate
? This is given by the
standard deviation of the estimator distribution We can calculate this
from the likelihood function if we recall that L is just the
probability for observing the sampled values x1,
x2,. . ., xn. Since
these values are used to calculate
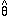 , L is related to
the distribution
for
, L is related to
the distribution
for 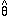 . Using (9), the
variance is then
. Using (9), the
variance is then
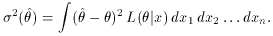
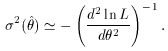
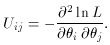
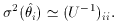
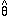 is the
theoretical
is the
theoretical  . This is a
desirable, but not
essential property for an estimator, guaranteed by the maximum
likelihood method only for infinite n. Estimators which have this
property are non-biased. We will see one example in the following
sections in which this is not the case. Equation (32), nevertheless,
remains valid for all
. This is a
desirable, but not
essential property for an estimator, guaranteed by the maximum
likelihood method only for infinite n. Estimators which have this
property are non-biased. We will see one example in the following
sections in which this is not the case. Equation (32), nevertheless,
remains valid for all 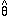 ,
since the error desired is the deviation from
the true mean irrespective of the bias.
,
since the error desired is the deviation from
the true mean irrespective of the bias.
 ), then the best estimate
of u can be shown to be
), then the best estimate
of u can be shown to be 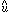 =
f(
=
f(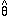 ).
).