


4.4 Estimators for the Gaussian Distribution
For a sample of n points, all taken from the same Gaussian distribution, the likelihood function is
Once again, taking the logarithm,
Taking the derivatives with respect to µ and
and
Solving (47) first yields
The best estimate of the theoretical mean for a Gaussian is thus the
sample mean, which again comes as no great surprise. From the general
result in (43), the uncertainty on the estimator is thus
This is usually referred to as the standard error of the mean. Note
that the error depends on the sample number as one would expect. As n
increases, the estimate
For the moment, however,
where we have replaced µ by its solution in (49). This, of
course, is just the sample variance.
For finite values of n, however, the sample variance turns out to be
a biased estimator, that is the expectation value of
s2 does not equal
the true value, but is offset from it by a constant factor. It is not
hard to show, in fact, that E[s2] =
Equation (52) is unbiased, however, it is no longer the best
estimate in the sense that its average deviation from the true value
is somewhat greater than that for (51). The difference is small
however, so that (52) still provides a good estimate. Equation
(52) then is the recommended formula for estimating the variance
Note that unlike the mean, it is impossible to estimate the standard
deviation from one measurement because of the (n - 1) term in the
denominator. This makes sense, of course, as it quite obviously
requires more than one point to determine a dispersion!
The variance of


 2 and setting them to 0,
we then have
2 and setting them to 0,
we then have




 becomes
more and more precise. When only one
measurement is made, n = 1,
becomes
more and more precise. When only one
measurement is made, n = 1,
 (
( ) reduces to
) reduces to  . For a
measuring device,
a thus represents the precision of the instrument.
. For a
measuring device,
a thus represents the precision of the instrument.
 is
still unknown. Solving (48) for
is
still unknown. Solving (48) for
 2
yields the estimator
2
yields the estimator

 2 -
2 -  2 / n = (n
- 1)
2 / n = (n
- 1)  2 /
n. Thus for n
very large, s2 approaches the true variance as
desired; however, for
small n,
2 /
n. Thus for n
very large, s2 approaches the true variance as
desired; however, for
small n,  2 is
underestimated by s2 The reason is quite simple: for
small samples, the occurrence of large values far from the mean is
rare, so the sample variance tends to be weighted more towards smaller
values. For practical use, a somewhat better estimate therefore,
would be to multiply (51) by the factor n / (n - 1),
2 is
underestimated by s2 The reason is quite simple: for
small samples, the occurrence of large values far from the mean is
rare, so the sample variance tends to be weighted more towards smaller
values. For practical use, a somewhat better estimate therefore,
would be to multiply (51) by the factor n / (n - 1),

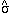 2 in (52)
may also be shown to be
2 in (52)
may also be shown to be