


2.2. Equations of motion
The hot big bang theory is based on the cosmological principle, which states that the Universe should look the same to all observers. That tells us that the Universe must be homogeneous and isotropic, which in turn tells us which metric must be used to describe it. It is the Robertson-Walker metric
Here t is the time variable, and r-
If no external forces are acting, then a particle at rest at a given set of
coordinates
(r,
The expansion of the Universe is governed by the properties of material
within it. This can be specified
(1) by the energy density
In general though there need not be a simple equation of state; for example
there may be more than one type of material, such as a combination of
radiation and non-relativistic matter, and certain types of material, such
as a scalar field (a type of material we'll encounter later which is
crucial for modelling inflation),
cannot be described by an equation of state at all.
The crucial equations describing the expansion of the Universe are
where overdots are time derivatives and
H =
These can also be combined to form a new equation
in which k does not appear explicitly.
1 I follow standard cosmological
practice of setting the fundamental constants c and
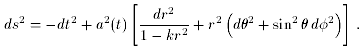
 -
- are (polar)
coordinates. The constant k measures the spatial curvature, with
k
negative, zero and positive corresponding to open, flat and closed
Universes respectively. If k is zero or negative, then the range of
r is from zero to infinity and the Universe is infinite, while
if k
is positive then r goes from zero to
1/
are (polar)
coordinates. The constant k measures the spatial curvature, with
k
negative, zero and positive corresponding to open, flat and closed
Universes respectively. If k is zero or negative, then the range of
r is from zero to infinity and the Universe is infinite, while
if k
is positive then r goes from zero to
1/ k. Usually the
coordinates are rescaled to make k equal to -1, 0 or +1. The
quantity a(t) is the scale-factor of the Universe, which
measures its
physical size. The form of a(t) depends on the properties of the
material within the Universe, as we'll see.
k. Usually the
coordinates are rescaled to make k equal to -1, 0 or +1. The
quantity a(t) is the scale-factor of the Universe, which
measures its
physical size. The form of a(t) depends on the properties of the
material within the Universe, as we'll see.
 ,
,
 ) will remain there. Such
coordinates are said
to be comoving with the expansion. One swaps between physical (ie
actual) and comoving distances via
) will remain there. Such
coordinates are said
to be comoving with the expansion. One swaps between physical (ie
actual) and comoving distances via
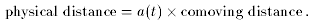
 (t) and the pressure p(t). These are often related by an equation of
state, which gives p as a function of
(t) and the pressure p(t). These are often related by an equation of
state, which gives p as a function of
 ; the classic examples are
; the classic examples are
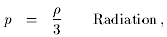
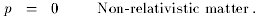


 / a is the Hubble
parameter. The terms in the fluid equation contributing to
/ a is the Hubble
parameter. The terms in the fluid equation contributing to
 have
a simple interpretation; the term
3H
have
a simple interpretation; the term
3H is the
reduction in density due
to the increase in volume, and the term 3Hp is the reduction in energy
caused by the thermodynamic work done by the pressure when this expansion
occurs.
is the
reduction in density due
to the increase in volume, and the term 3Hp is the reduction in energy
caused by the thermodynamic work done by the pressure when this expansion
occurs.
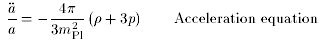
 equal to one.
This makes the energy density and mass density interchangeable (since the
former is c2 times the latter). I shall also normally
use the Planck mass
mPl rather than the gravitational constant G;
with the convention just
mentioned they are related by
G
equal to one.
This makes the energy density and mass density interchangeable (since the
former is c2 times the latter). I shall also normally
use the Planck mass
mPl rather than the gravitational constant G;
with the convention just
mentioned they are related by
G  mPl-2. Back.
mPl-2. Back.