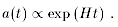Seen with many years of hindsight, the idea of inflation is actually rather obvious. Take for example the Friedmann equation as used to analyze the flatness problem
The problem with the hot big bang model is that aH always
decreases, and
so
In order to solve the problem, we will clearly need to reverse this
state of affairs. Accordingly,
define inflation to be any epoch where
The middle definition is the one which I prefer to use,
because it has the most direct
geometrical interpretation. It says that the Hubble length, as measured in
comoving coordinates, decreases during inflation. At any other time,
the comoving Hubble length increases. This is the key property of inflation;
although typically the expansion of the Universe is very rapid, the crucial
characteristic scale of the Universe is actually becoming smaller, when
measured relative to that expansion.
As we will see, quite a wide range of behaviours satisfy the
inflationary condition. The most classic one is one we have already
seen; when the equation of state is p = -
Since the successes of the hot big bang theory rely on the Universe
having a conventional (non-inflationary) evolution, we cannot permit
this inflationary period to go on forever - it must come to an end
early enough that the big bang successes are not threatened. Normally,
then, inflation is viewed as a phenomenon of the very early Universe,
which comes to an end and is followed by the conventional behaviour.
Inflation does not replace the hot big bang theory; it is a bolt-on
accessory attached at early times to improve the performance of the
theory.
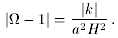
 is repelled away from one.
is repelled away from one.
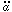 > 0, an
accelerated expansion. We can rewrite this in several different ways
> 0, an
accelerated expansion. We can rewrite this in several different ways
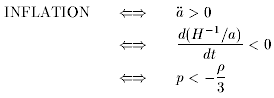
(27)
(28)
(29)
 , the solution is
, the solution is