4.3. The horizon problem and homogeneity
The inflationary expansion also solves the horizon problem. The basic strategy is to ensure that
so that light can travel much further before decoupling than it can afterwards. This cannot be done with standard evolution, but can be achieved by inflation.
An alternative way to view this is to remember that inflation corresponds to a decreasing comoving Hubble length. The Hubble length is ordinarily a good measure of how far things can travel in the Universe; what this is telling us is that the region of the Universe we can see after (even long after) inflation is much smaller than the region which would have been visible before inflation started. Hence causal physics was perfectly capable of producing a large smooth thermalized region, encompassing a volume greatly in excess of our presently observable Universe. In Figure 2, the outer circle indicates the initial Hubble length, encompassing the shaded smooth patch. Inflation shrinks this dramatically inwards towards the dot indicating our position, and then after inflation it increases while staying within the initial smooth patch. (3)
|
Figure 2. Solving the horizon problem. Initially the Hubble length is large, and a smooth patch forms by causal interactions. Inflation then shrinks the Hubble length, and even the subsequent expansion again after inflation leaves the observable Universe within the smoothed patch. |
Equally, causal processes would be capable of generating irregularities in the Universe on scales greatly exceeding our presently observable Universe, provided they happened at an early enough time that those scales were within causal contact. This will be explored in detail later.
3 Although this
is a standard description, it isn't totally accurate. A more accurate
argument is as follows.
[2] At the
beginning of inflation
particles are distributed in a set of modes. This may be a thermal
distribution or something else; whatever, since the energy density is
finite there will be a shortest wavelength occupied mode, e.g. for a
thermal distribution
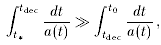
max ~
1/T. Expressed in
physical coordinates, once inflation has stretched all modes including
this one to be much larger than the Hubble length, the Universe becomes
homogeneous. In comoving coordinates, the equivalent picture is that
the Hubble length shrinks in until it's much smaller than the shortest
wavelength, and the Universe, as before, appears homogeneous.
Back.