5.1. Scalar fields and their potentials
In particle physics, a scalar field is used to represent spin zero particles. It transforms as a scalar (that is, it is unchanged) under coordinate transformations. In a homogeneous Universe, the scalar field is a function of time alone.
In particle theories, scalar fields are a crucial ingredient for spontaneous symmetry breaking. The most famous example is the Higgs field which breaks the electro-weak symmetry, whose existence is hoped to be verified at the Large Hadron Collider at CERN when it commences experiments next millennium. Scalar fields are also expected to be associated with the breaking of other symmetries, such as those of Grand Unified Theories, supersymmetry etc.
The traditional starting point for particle physics models is the
action, which is an integral of the Lagrange density over space and time
and from which the equations of motion can be obtained. As an
intermediate step, one might write down the energy-momentum tensor,
which sits on the right-hand side of Einstein's equations. Rather than
begin there, I will take as my starting point expressions for
the effective energy density and pressure of a homogeneous scalar
field, which I'll call 
. These are
obtained by comparison of the
energy-momentum tensor of the scalar field with that of a perfect
fluid, and are
One can think of the first term in each as a kinetic energy, and the
second as a potential energy. The potential energy
V(
Note in passing that a scalar field cannot in general be described by an
equation of state; there is no unique value of p that can be associated
with a given
In a given theory, there would be a specific form for the potential
V(
The strength of this approach is that it seems possible to capture many of
the crucial properties of inflation by looking at some simple potentials;
one is looking for results which will still hold when more `realistic'
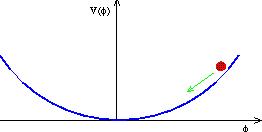
potentials are chosen. Figure 3 shows such a generic
potential,
with the scalar field displaced from the minimum and trying to reach it.
Figure 3. A generic inflationary potential.
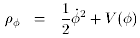
(33)
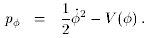
(34)
) can be
thought of as a form of `configurational' or `binding' energy; it
measures how much internal energy is associated with a particular field
value. Normally, like all systems, scalar fields try to minimize this
energy; however, a crucial ingredient which allows inflation is that
scalar fields are not always very efficient at reaching this minimum
energy state.
as the
energy density can be divided between potential
and kinetic energy in different ways.
), at least up to some
parameters which one could hope to measure
(such as the effective mass and interaction strength of the scalar field).
However, we are not presently in a position where there is a well
established fundamental theory that one can use, so, in the absence of such
a theory, inflation workers tend to regard
V() as a function to be
chosen arbitrarily, with different choices corresponding to different models
of inflation (of which there are many). Some example potentials are
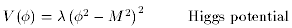
(35)
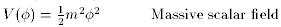
(36)
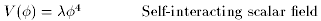
(37)
