


6.4. Testing the idea of inflation
The moral of the previous section was that different inflation models lead to very different models of structure formation, spanning a wide range of possibilities. That means, for example, that a definite measure of say the spectral index n would rule out most inflation models. But it would always be possible to find models which did give that value of n. Is there any way to try and test the idea of inflation, independently of the model chosen?
The answer, in principle, is yes. In the previous section we introduced
three observables (in addition to the overall normalization), namely n,
R and
nG. However, they depend only on two fundamental
parameters, namely  and
and
 .
[3] We can therefore
eliminate
.
[3] We can therefore
eliminate  and
and
 to obtain a relation
between observables, the consistency equation
to obtain a relation
between observables, the consistency equation
This relation has been much discussed in the literature.
[26,
21]
It is independent of the choice of inflationary model (though it does
rely on the slow-roll and power-law approximations).
The idea of a consistency equation is in fact very general. The point is
that we have obtained two continuous functions,
Vindication of the consistency equation would be a remarkably convincing
test of the inflationary paradigm, as it would be highly unlikely that
any other production mechanism could entangle the two spectra in the way
inflation does. Unfortunately though, measuring
nG is a much
more challenging observational task than measuring n or R and is
likely to be
beyond even next generation observations. Indeed, this is a good point
to remind the reader that even if inflation is right, only one model can
be right and it is perfectly possible (and maybe even probable, see
Ref.
[27])
that that model has a very low amplitude of
gravitational waves and that they will never be detected.
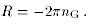
 H(k) and
AG(k), from a single continuous function
V(
H(k) and
AG(k), from a single continuous function
V( ). This
can only be possible if the functions
). This
can only be possible if the functions
 H(k) and
AG(k) are related,
and the equation quoted above is the simplest manifestation of such a
relation.
H(k) and
AG(k) are related,
and the equation quoted above is the simplest manifestation of such a
relation.