


4.2. Deviations from the power-law
The power-law approximation to the spectra, as derived in Ref. [23], is particularly good at the moment because the available observations are not very accurate. In most models the spectra are indistinguishable from power laws even at PLANCK accuracy, but there are exceptions, and if deviations are observable they correspond to extra available information on the inflationary spectrum [26, 27]. One such class of models are models where features have been deliberately inserted into the potential in order to generate sharp features in the power spectrum, such as the broken scale-invariance models.
However, even without a specific feature, it may be possible to see
deviations, if the slow-roll approximation is not particularly good.
There is actually modest theoretical prejudice in favour of this,
because in supergravity models the inflaton is expected to receive
corrections to its mass which are large enough to threaten slow-roll
[3].
Specifically, the slow-roll parameter
 , which is supposed to be
small, receives a contribution of
, which is supposed to be
small, receives a contribution of
where the `something' is model dependent. It is clear that if slow-roll
is to be very good,
If we accept that, then we conclude that n should not be extremely
close to one (which would exacerbate the need for cancellation), and also
that the deviation from scale-invariance, dn / d
ln k, which is given by the
slow-roll parameters, might be large enough to be measurable
[27].
A specific example where this is indeed the case is the running mass model
[28,
29].
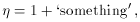
 << 1, then the
`something' has to cancel the
`1' to quite high accuracy, and there is no theoretical motivation
saying it should.
<< 1, then the
`something' has to cancel the
`1' to quite high accuracy, and there is no theoretical motivation
saying it should.