


3.2. Scalar fields and their potentials
In order to obtain the required equation of state, a suitable material
must come to dominate the density of the Universe. Such a material is
a scalar field, which in particle physics is used to represent
spin-zero particles and which we represent by
 throughout. It
transforms as a scalar (that is, it is unchanged) under coordinate
transformations. In a homogeneous Universe, the scalar field is a
function of time alone.
throughout. It
transforms as a scalar (that is, it is unchanged) under coordinate
transformations. In a homogeneous Universe, the scalar field is a
function of time alone.
At present no fundamental scalar field has been observed, but they proliferate in modern particle physics theories. In particular, supersymmetry associates a boson with every fermion (and vice versa), giving a multitude of scalar fields in any supersymmetric theory containing the Standard Model of particle physics.
The traditional starting point for particle physics models is the action, which is an integral of the Lagrange density over space and time and from which the equations of motion can be obtained. As an intermediate step, one might write down the energy-momentum tensor, which sits on the right-hand side of Einstein's equations. Rather than begin there, I will take as my starting point expressions for the effective energy density and pressure of a homogeneous scalar field. These are obtained by comparison of the energy-momentum tensor of the scalar field with that of a perfect fluid, and are
One can think of the first term in each as a kinetic energy, and the
second as a potential energy. The potential energy
V(
Note in passing that a scalar field cannot in general be described by
an equation of state; there is no unique value of p that can be
associated with a given
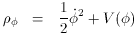
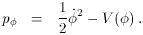
 ) can be
thought of as a form of `configurational' or `binding' energy; it
measures how much internal energy is associated with a particular
field value (including the mass-energy of the particle number density
it represents). Normally, like all systems, scalar fields try to
minimize this energy; however, a crucial ingredient which allows
inflation is that scalar fields are not always very efficient at
reaching this minimum energy state.
) can be
thought of as a form of `configurational' or `binding' energy; it
measures how much internal energy is associated with a particular
field value (including the mass-energy of the particle number density
it represents). Normally, like all systems, scalar fields try to
minimize this energy; however, a crucial ingredient which allows
inflation is that scalar fields are not always very efficient at
reaching this minimum energy state.
 as the energy
density can be divided
between potential and kinetic energy in different ways. This is not
particularly significant for early Universe inflation, but will be
later when we discuss the present Universe.
as the energy
density can be divided
between potential and kinetic energy in different ways. This is not
particularly significant for early Universe inflation, but will be
later when we discuss the present Universe.