IRAS has shown us that the far-infrared emission of galaxies in the local universe constitutes a large fraction, ~ 30%, of the total energy output of normal galaxies, and that for some starburst and active galaxies the far-infrared fraction can be much higher (see Lonsdale 1992 and references therein). It follows by analogy to derivations of the expected integrated light in the optical band (e.g., Partridge and Peebles 1967) that the integrated light of galaxies in the infrared region can be expected to be at least a few percent of the peak of the CMB. Hacking, Condon and Houck (1987) found evidence for strong luminosity and/or density evolution of IRAS galaxies, at a rate comparable to that of quasars, which further enhances the expected integrated background radiation (see also Franceschini et al. 1988b; Lonsdale and Hacking 1989; Lonsdale et al. 1990; Saunders et al. 1990; Hacking and Soifer 1991).
The simplest kind of model for the integrated emission of galaxies involves taking a local luminosity function (LF) and a functional form for the evolutionary law, and extrapolating backwards in time to match the observed flux and redshift distributions of deep galaxy samples in a particular wavelength band. The model distributions are then integrated over flux and redshift, to some maximum redshift, zmax, to derive a background intensity. In many models the entire luminosity function is fixed in shape and it translates en masse in luminosity and/or density at the given rate. Such models are called translational models, and they were originally proposed for the evolution of radio sources and quasars. The physical interpretation of such evolution involved an increasing luminosity of AGN with lookback time for luminosity evolution, or an increasing fraction of galaxies possessing AGN at earlier times for density evolution. In the context of far-infrared bright galaxies, power law translational evolution would describe an increasing luminosity of starbursts and/or AGN with lookback time, or an increasing fraction of galaxies undergoing starburst episodes and/or AGN events with lookback time. Thus this kind of evolution is not well suited for describing the recently popular merging scenarios, in which smaller galaxies merge to form larger ones - such scenarios implicitly involve evolution of the shape of the luminosity function.
A summary of the parametric models of the far-infrared background that
have been
published based on translational evolution is given in the upper panel
of Table 1. The
wavelengths or wavelength range modeled, the cosmology, and
zmax adopted by these
various authors is given. The parameters
,
,
and Q define the parametric form of
the assumed evolution behavior of the LF with redshift, as follows:
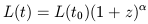
| (1) |
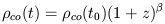
| (2) |
describing power law luminosity and density evolution, respectively,
where 
co is the
co-moving density, and:
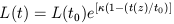
| (3) |
for exponential luminosity evolution. For
= 1, (t(z) /
t0) = (1 + z)-3/2 defining the
relation used by
Oliver et al. (1992):
L(t) = L(t0) exp{2/3Q[1 - (1 +
z)-3/2]}.
For the first four models in Table 1 all galaxies
comprising the LF are allowed evolve at the same rate, while the model of
Franceschini et
al. (1991)
allows for three galaxies
types to evolve at different rates. The model of Treyer and Silk is
different in nature
from the others in that they do not allow the luminosity function of
"normal" galaxies
to evolve with time, but add a new population of dwarf galaxies whose
characteristic
space density, 
*
(Mpc-3), is the parameter that evolves:
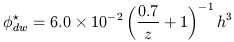
| (4) |
where h = H0 in units of 100 km/s/Mpc. This model is designed to explain the steepness of the observed blue number counts of galaxies with a population of dwarf galaxies which is present at z = 0.7 but has faded to invisibility by the current epoch. Treyer and Silk also investigate a model based on the number density evolution of dark matter halos in a cold dark matter scenario, which predicts a large abundance of low-mass halos. The integrated background light produced by this model is very similar to that of the blue dwarf model described by equation (4).
A different kind of model assumes that the evolution with lookback time of galaxies in the far-infrared is principally due to the natural evolution of their stellar populations and interstellar medium, without necessarily invoking dramatic starburst or AGN events. The most sophisticated kind of model involves population synthesis using stellar photometric and chemical evolution prescriptions to model in detail the spectral energy distributions of various galaxy types as a function of time. The evolutionary behavior of models of this type is usually dictated by an assumed dependence of the star formation rate on some power of the gas mass or density. As for the purely parametric LF translational models, the synthesis models are matched to the flux and redshift distributions of deep galaxy samples and then integrated to derive backgrounds.
| Model | 
| H0 |
| zmax | ,
,
, Q
| Figure |
| (µm) | ||||||
| Weedman 1990 | 100 | 75 | 0.1 | 4 | = 2.5 | 4 |
| Hacking and Soifer 1991 | 25, 60, 100 | 75 | 1 | 0.5 | = 4
| 4 |
| 3 | = 2,3
| |||||
| Beichman and Helou 1991 | 10-1000 | 40-100 | 0-1 | 1-5 | = 2,4
| 4 |
| Oliver et al. 1992 | 4-1500 | 50 | 1 | 1-7 | = 3.15 | 5 |
| = 6.7
| ||||||
| Q = 3.2 | ||||||
| Franceschini et al. 1991 | 12-1000 | 50 | 0.1 | 5 | normal galaxies:
= 0 | 4 |
| starbursts: = 3.2 | ||||||
| AGN: = 2.5 | ||||||
| Treyer and Silk 1993 | 12-550 | 50 | 1 | see text | 4 | |
| Wang 1991b | 20-1000 | 50 | 1 | 2,5,20 | 6 | |
| Franceschini et al. 1993 | 20-1000 | 50 | 1 | 4.5 | 6 | |
Population synthesis modeling of evolving galaxies is a very active field in the UV through near-infrared bands, but it is less well developed at far-infrared wavelengths because the dust re-emission of stellar photons is an extra dimension which most modelers have yet to tackle. The population synthesis models of Mazzei, Xu and de Zotti (1992) and Mazzei, De Zotti and Xu (1993) are the first to fully incorporate the re-emission of starlight by dust within galaxies. These closed box models incorporate chemical evolution, thus at early epochs the dust content grows with time as the metallicity increases with the return to the interstellar medium of enriched gas from evolved stars. The dust optical depth reaches a maximum and some point in time and then declines again as star formation gradually uses up the ISM.
The rate of change of the dust opacity is a function of the initial star
formation
rate, which is largest for the earliest type galaxies and smallest for
the latest types. The
behavior of 
with time is
illustrated for several galaxy types in Figure 2:
a much more
rapid relative far-infrared/optical-UV evolution is expected with
lookback time for early
type than for late-type systems, because the latest type systems are
still reaching their
peak optical depth at the present epoch. Late-type systems in the local
universe do
indeed emit similar amounts of energy in the optical-UV and the
far-infrared, whereas
ellipticals now emit only a very small fraction of their energy in the
far-infrared.
|
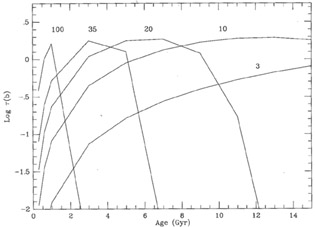
Figure 2. Optical depth in the blue from
Mazzei et
al. (1992).
The curves are labeled by the initial star formation rate
(M |
In Figure 3, I reproduce a figure from Mazzei and de Zotti (1993), which shows model spectral energy distributions for a range of ages for elliptical galaxies, compared to the observed data for the high redshift IRAS galaxy F10214+4724 (see Section 3.1 for a discussion of this object). The oldest of these models represents a present day elliptical, and matches observations of local ellipticals well (Mazzei et al. 1993). This figure clearly illustrates the expected very strong evolution in the shape of the spectral energy distribution (SED), with a far higher percentage of the total energy emerging at far-infrared wavelengths at early times than today.
|
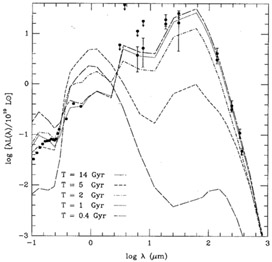
Figure 3. Evolution of the spectral energy
distribution of an elliptical galaxy
(Mazzei et al. 1993)
compared to the observed spectrum of IRAS F10214+4724 at z = 2.286
(reproduced from
Mazzei and De
Zotti 1993).
This model has a
Salpeter (1955) IMF
with a lower mass limit of 0.5
M |
Two models based on the natural chemical and photometric evolution of stellar populations and interstellar medium are summarized in the lower panel of Table 1. Franceschini et al. (1991) have used the models of Mazzei et al. to predict the cosmological background due to evolving galaxies in the near and mid-infrared, however in the far-infrared region they revert to a power law parametric approach similar to those discussed above. This approach is improved in Franceschini et al. (1993), who extend the synthesis modeling to the far-infrared. They obtain good fits to the local 60µm counts with their model, due for the most part to the strong dust evolution of early-type systems. Chokshi et al. (1993) have used the models of Mazzei et al. (1992) to simulate deep blue and near-infrared galaxy images, and Chokshi et al. (1994, in preparation) will extend their approach to a full spectral synthesis modeling at far-infrared wavelengths.
Wang (1991a, b) has also considered the evolution of the dust and the far-infrared emission from disk galaxies with time, and their contribution to the far-infrared background. Taking an analytical rather than a population synthesis approach, Wang derives the chemical evolution for a prompt initial enrichment (PIE) model and also for an accretion model, and the subsequent evolution of the interstellar dust, which he argues forms principally in molecular clouds. Wang finds that the dust content of young disk galaxies can be up to 4 times larger than today, and the far-infrared luminosity can be two orders of magnitude greater. The PIE model predicts much stronger backgrounds than the accretion model because it shows strong evolution of the dust mass.
The results of the various parametric LF translational evolution models for the infrared background emission are summarized in Figures 4 and 5. The Beichman and Helou (1991) models selected for this figure bracket all their models, and incorporate an improved treatment of the energy distributions of local galaxies compared to the models in the published paper (G. Helou, private communication).
|
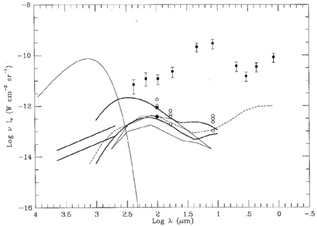
Figure 4. Comparison of various
translational evolution models for the integrated light
of galaxies to the COBE data. Heavy solid lines -
Beichman and Helou
(1991)
no-evolution model, H0 = 40, q = 0.25 (lower),
and density evolution model,
|
Most of the parametric models summarized in Table 1 do not conflict with the currently available DIRBE limits, however the higher evolutionary rates and the higher values for zmax are constrained by the longest wavelength DIRBE limits, in particular the higher zmax density evolution models of Oliver et al. are inconsistent with the DIRBE limits.
|
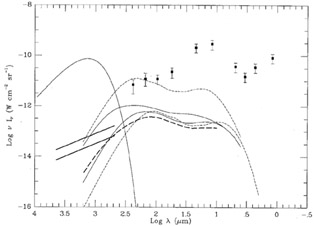
Figure 5. Comparison of
Oliver et al.'s
(1992)
translational evolution models for the
integrated light of galaxies to the COBE data. Dashed lines - density
evolution, zmax =
1.0 (lower) and zmax = 2.16 (upper); Heavy dashed line -
exponential luminosity
evolution, Q = 3.2, zmax = 6.94; Light solid
lines - power law luminosity evolution,
|
The FIRAS distortion limits provide a much stronger constraint,
particularly the
lower line with the galactic foreground removed by Mather et al. As
noted above,
however, this limit may be too stringent for comparison to the evolving
galaxy models, since
a portion of the "galactic foreground" that has been removed by
Mather et al. (1993)
may be part of an isotropic extragalactic background due to the
integrated light of galaxies
(Wright et al. 1993).
Even our approximate estimate of the FIRAS limit using
Wright et al.'s more conservative csc|b| galactic foreground
subtraction constrains the
evolving models quite strongly, ruling out the parametric power
luminosity evolution
models with values of high
enough to fit the 60µm number counts
( ~ 3 - 4). Thus
if pure power law luminosity evolution is the explanation for the
steepness of the local universe 60µm number counts, then
this evolution cannot continue to cosmological
distances without severely violating the FIRAS distortion limits. There
is some evidence that power law luminosity evolution with
> 2 is also ruled out by the
redshift
distributions of IRAS 60 and 100µm-selected galaxy samples
(Hacking and Soifer
1991;
Fisher et al. 1992).
The power law density evolution models which can fit the
60µm number counts,
~4 - 7, are only
consistent with FIRAS for very low values of zmax;
zmax << 2.2 for
the Oliver et al. models. This is because higher evolutionary rates are
needed to fit the
z < 0.5 number counts using power law density evolution than power law
luminosity
evolution. Since this form of translational density evolution involves a
scenario in which
the fraction of galaxies having starbursts and/or AGN increases with
lookback time, a
low value for zmax is necessary, in any case, to prevent this
starbursting (and/or AGN)
population from becoming larger than the total galaxy population
(Weedman 1990;
Hacking and Soifer
1991).
The exponential luminosity evolution models fare somewhat better: both the
Franceschini et
al. (1991)
model with zmax = 5 and the Oliver et al. model with
zmax = 6.9,
which can fit the local number counts with
~ 2 - 3, are consistent with the
upper FIRAS line, though the Oliver et al. model is only barely
consistent with the lower
of the two FIRAS lines. This difference from the power law luminosity
evolution models
is not surprising since exponential evolution was introduced to avoid
the high-redshift divergence of power-law evolution
(Rowan-Robinson
1968).
Wright et al. (1993)
fitted the distortion limits with a
< 2.3
(2
) exponential
model based on the Beichman and Helou models, after subtracting the
conservative
csc|b| contribution due to the Galaxy that they do not believe
likely to include a
significant extragalactic component (approximated by the upper FIRAS
deviation line in
figures 4 and 5). They
estimate that this translates to an upper limit on the fraction of
the baryon density converted from He to H by such a population of
evolving infrared galaxies of < 0.8%.
The fading dwarf model of Treyer and Silk is also comfortably consistent with the FIRAS limits, which is not surprising given that this model assigns most of evolutionary effect to dwarf galaxies at relatively low redshifts.
As noted above, all of the pure translational evolution models are limited in that they allow only translational evolution of the entire LF; they do not allow evolution of any other physical galaxy property, including the dust temperature. Most of them do not treat different galaxy types separately. Given that these models are now coming into direct conflict with the COBE results, it is clear that that the more sophisticated chemical evolution-based models are necessary to get a more realistic understanding of the integrated emission of galaxies in the far-infrared. In particular, it is important to recognize the likely importance of strong evolution of the dust optical depth in early type systems. Such models of course have their own shortcomings, most notably the fact that they have many more physical variables than can be realistically constrained by observables at present. None-the-less they represent the best approach in the long run since the universe contains these parameters, whether we can measure then now or not!
Figure 6 illustrates the results of the two models based on the natural chemical and photometric evolution of stellar populations and interstellar medium described above. The two models of Wang (1991b) shown in Figure 6 bracket all those displayed in his Figure 2 for zf = 5. Some of these models are also strongly limited by the FIRAS distortion results, in particular the PIE models of Wang with exponentially declining star formation rate. The conflict with the FIRAS data would be lower for the lower zf PIE model of Wang (zf = 2). The accretion models of Wang are in more acceptable agreement, since they show little evolution of the dust mass with lookback time. Note that the models of Wang have not been constrained to fit the observed local universe far-infrared number counts, unlike the parametric translational models discussed above, and the models of Franceschini et al. (1993). The opaque model of Franceschini et al. (1993) is also marginally in conflict with the more stringent of the two FIRAS limits.
|
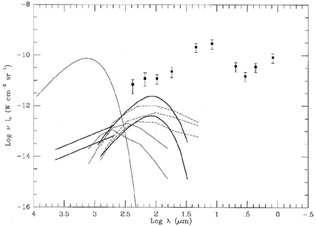
Figure 6. Comparison of various models for
the integrated light of galaxies and
protogalaxies to the COBE data. Heavy solid lines -
Wang (1991b)
zf = 5 PIE model
with exponentially decreasing star formation rate (upper),
zf = 5 accretion model with
constant star formation rate (lower). Dashed lines -
Franceschini et
al. (1993)
population synthesis no-evolution (lower), moderately opaque (middle)
and opaque (upper) models. Light solid lines -
Franceschini et
al. (1991)
protogalaxy models with zf = 4.3,
|
A constraint on the dust content and temperature of young disk galaxies
has been derived by
Fall and Pei (1993),
who have estimated the dust density of the damped
Ly systems, which may be the
progenitors of present-day galactic disks, from the
observed reddening of quasars seen on the line-of-sight through the
damped Ly systems.
From this dust density they can then estimate the contribution of these
disks to the
far-infrared and submillimeter background in a simple way, with the
(unknown) dust
temperature as the only important variable. They find limits on the
co-moving dust
density in the damped Ly
systems of 10-6 < h
dust <
10-4. Using the then available
FIRAS and DIRBE limits, these dust densities translated to limits on the dust
temperature in the disks of < 60K and < 25K for h
dust =
10-6 and 10-4, respectively,
based on an integration of the damped
Ly systems between redshifts of
2 and 3, where they are observed. The newer FIRAS limits of
Mather et al. (1993)
would lower these temperature limits somewhat. This is an interesting
technique, though it is limited by
definition to low optical depth lines-of-sight through the foreground
systems, thus can
tell us little of any denser star forming regions in young disk
galaxies. It can also tell
us nothing of the dust masses and temperatures in ellipticals and S0s at
high redshift,
and these are the systems that are most likely to be the most important
far-infrared emitters at early epochs.
Some additional constraints on evolving galaxy models can be sought at other
wavelengths. In the radio a strong correlation in evolutionary behavior
may be expected
because of the well-known strong correlation between far-infrared and
radio fluxes for most types of radio-quiet galaxies (e.g.,
Helou, Soifer and
Rowan-Robinson 1985).
A historical anecdote is of interest here. Far-infrared evolution
studies are presently based
on IRAS data, and when IRAS was launched few people dreamed it would be
sensitive
enough to tackle cosmological questions realistically! In fact what
motivated Perry Hacking to address this question for his thesis
(Hacking 1987;
Hacking, Condon and
Houck 1987)
was the realization that if, because of the radio-infrared correlation,
galaxies
evolved as much in the far-infrared as they apparently do at cm radio
wavelengths
(L 
(1 +
z)~4,
Condon 1984)
then such strong evolution should be detectable by
IRAS, even though it only probed to modest redshifts (z
0.1). The result of Hacking's
study was the conclusion that the faint IRAS 60µm counts
could be fitted reasonably
well with the same model that was found to best fit the counts for the
sub-millijansky
radio source population (i.e., the non-active galaxy radio source
population) by
Condon (1984).
Similar conclusions have been reached by other authors using different models (e.g., Danese et al. 1987; Treyer and Silk 1993; Franceschini et al. 1993), therefore it seems clear that in the relatively local universe at least, the radio and far-infrared number counts and redshift distributions of non-active galaxies can be used together to constrain evolutionary scenarios. Unfortunately, for cosmological background studies the radio wavelength region is considerably less interesting that the far-infrared, as Malcolm Longair describes eloquently elsewhere in this volume.
There has been some work addressing the implications of evolving far-infrared bright galaxies to the X-ray background (Weedman 1990; Griffiths and Padovani 1990; Lonsdale and Harmon 1991; Treyer and Silk 1993). These studies conclude that the simplest parametric models which fit the far-infrared number counts can produce 50 to 100% of the soft X-ray background. Since much, if not all, of the soft X-ray background seems to be due to AGNs, the actual contribution from starbursting infrared-bright galaxies must be no more than 50% and probably lower. This constraint is likely to prove interesting as evolving models become more sophisticated.
/ yr).
z = 0.3 (lower),
zf = 2