


The history of the transition from a neutral universe to one that is almost
fully ionized can reveal the character of cosmological ionizing sources
and constrain the star formation activity at high redshifts.
The existence of a filamentary, low-density intergalactic medium (IGM), which
contains the bulk of the hydrogen and helium in the universe, is predicted
as a product of primordial nucleosynthesis
[8] and of hierarchical
models of gravitational instability with ``cold dark matter'' (CDM)
[6],
[26].
The application of the Gunn-Peterson constraint on
the amount of smoothly distributed neutral material along the line of sight
to distant objects requires the hydrogen component of the diffuse IGM to
have been highly ionized by z  5
[49], and the helium
component by z
5
[49], and the helium
component by z  2.5
[9].
From QSO absorption studies we also
know that neutral hydrogen accounts for only a small fraction, ~ 10%,
of the nucleosynthetic baryons at early epochs
[29]. It thus appears
that substantial sources of ultraviolet photons were present at z
2.5
[9].
From QSO absorption studies we also
know that neutral hydrogen accounts for only a small fraction, ~ 10%,
of the nucleosynthetic baryons at early epochs
[29]. It thus appears
that substantial sources of ultraviolet photons were present at z
 5,
perhaps low-luminosity quasars
[22]
or a first generation of stars in
virialized dark matter halos with Tvir ~
104-105 K
[40],
[21],
[38].
The existence of a decline in the space density of bright quasars at redshifts
beyond ~ 3 was first suggested by
[39], and has
been since then
the subject of a long-standing debate. In recent years, several optical
surveys have consistently provided new evidence for a turnover in the QSO
counts [23],
[57],
[48],
[28].
The interpretation of the drop-off observed in optically selected samples is
equivocal, however, because of the possible bias introduced by dust
obscuration arising from intervening systems. Radio emission, on the other
hand, is unaffected by dust, and it has recently been shown
[50] that
the space density of radio-loud quasars also decreases strongly for
z > 3.
This argues that the turnover is indeed real and that dust along the line of
sight has a minimal effect on optically-selected QSOs
(Figure 4, left panel).
The QSO emission rate of hydrogen ionizing photons per unit comoving volume is
shown in Figure 4 (right panel)
[34]. It
is important to notice that the procedure
adopted to derive this quantity implies a large correction for incompleteness
at high-z. With a fit to the quasar luminosity function (LF)
which goes as
5,
perhaps low-luminosity quasars
[22]
or a first generation of stars in
virialized dark matter halos with Tvir ~
104-105 K
[40],
[21],
[38].
The existence of a decline in the space density of bright quasars at redshifts
beyond ~ 3 was first suggested by
[39], and has
been since then
the subject of a long-standing debate. In recent years, several optical
surveys have consistently provided new evidence for a turnover in the QSO
counts [23],
[57],
[48],
[28].
The interpretation of the drop-off observed in optically selected samples is
equivocal, however, because of the possible bias introduced by dust
obscuration arising from intervening systems. Radio emission, on the other
hand, is unaffected by dust, and it has recently been shown
[50] that
the space density of radio-loud quasars also decreases strongly for
z > 3.
This argues that the turnover is indeed real and that dust along the line of
sight has a minimal effect on optically-selected QSOs
(Figure 4, left panel).
The QSO emission rate of hydrogen ionizing photons per unit comoving volume is
shown in Figure 4 (right panel)
[34]. It
is important to notice that the procedure
adopted to derive this quantity implies a large correction for incompleteness
at high-z. With a fit to the quasar luminosity function (LF)
which goes as
 (L)
(L)  L-1.64 at the faint end
[43], the
contribution to the emissivity converges rather slowly, as
L0.36. At
z = 4, for example, the blue magnitude at the break of the LF is
M*
L-1.64 at the faint end
[43], the
contribution to the emissivity converges rather slowly, as
L0.36. At
z = 4, for example, the blue magnitude at the break of the LF is
M*  -25.4, comparable or slightly fainter than the limits of current
high-z QSO surveys. A large fraction, about 90% at z = 4
and even higher at
earlier epochs, of the ionizing quasar emissivity is therefore
produced by sources that have not been actually observed, and are
assumed to be present based on an extrapolation from lower redshifts.
-25.4, comparable or slightly fainter than the limits of current
high-z QSO surveys. A large fraction, about 90% at z = 4
and even higher at
earlier epochs, of the ionizing quasar emissivity is therefore
produced by sources that have not been actually observed, and are
assumed to be present based on an extrapolation from lower redshifts.

| 
|
Figure 4. Left: comoving
space density of bright QSOs as a
function of redshift. The data points with error bars are taken from
[23]
(filled dots),
[57]
(filled squares),
[48]
(crosses), and
[28]
(filled pentagon).
The empty triangles show the space density of the Parkes flat-spectrum
radio-loud quasars with P > 7.2 x 1026 W
Hz-1 sr-1
[25].
Right: comoving emission rate of hydrogen Lyman-continuum
photons (solid line) from QSOs, compared with the minimum rate
(dashed line) which is needed to fully ionize a fast recombining (with
gas clumping factor C = 30) Einstein-de Sitter universe with
| |
Galaxies with ongoing star-formation are another obvious source of Lyman
continuum photons. Since the
rest-frame UV continuum at 1500 Å (redshifted into the visible band for a
source at z  3) is
dominated by the same short-lived, massive stars
which are responsible for the emission of photons shortward of the Lyman edge,
the needed conversion factor, about one ionizing photon every 10 photons at
1500 Å, is fairly insensitive to the assumed IMF and is independent of the
galaxy history for t >> 107 yr.
Figure 4 shows the estimated
Lyman-continuum luminosity density of galaxies at z
3) is
dominated by the same short-lived, massive stars
which are responsible for the emission of photons shortward of the Lyman edge,
the needed conversion factor, about one ionizing photon every 10 photons at
1500 Å, is fairly insensitive to the assumed IMF and is independent of the
galaxy history for t >> 107 yr.
Figure 4 shows the estimated
Lyman-continuum luminosity density of galaxies at z  3. (2)
The data point assumes a value of
fesc = 0.5 for the unknown fraction of ionizing
photons which escapes the galaxy HI layers into the intergalactic medium.
A substantial population of dwarf galaxies below the detection threshold,
i.e. having star-formation rates < 0.3 M
3. (2)
The data point assumes a value of
fesc = 0.5 for the unknown fraction of ionizing
photons which escapes the galaxy HI layers into the intergalactic medium.
A substantial population of dwarf galaxies below the detection threshold,
i.e. having star-formation rates < 0.3 M yr-1
Mpc-3, and with a space density in excess of
that predicted by extrapolating to faint magnitudes the
yr-1
Mpc-3, and with a space density in excess of
that predicted by extrapolating to faint magnitudes the  = 1.38 best-fit
Schechter function, may be expected to form at early times in hierarchical
clustering models, and has been recently proposed by
[38] and
[34]
as a possible candidate for photoionizing the IGM at these
epochs. One should note that, while highly reddened galaxies at high
redshifts would be missed by the dropout color technique (which isolates
sources that have blue colors in the optical and a sharp drop in the
rest-frame UV), it seems unlikely that very dusty objects (with
fesc << 1) would contribute in any significant manner
to the ionizing metagalactic flux.
= 1.38 best-fit
Schechter function, may be expected to form at early times in hierarchical
clustering models, and has been recently proposed by
[38] and
[34]
as a possible candidate for photoionizing the IGM at these
epochs. One should note that, while highly reddened galaxies at high
redshifts would be missed by the dropout color technique (which isolates
sources that have blue colors in the optical and a sharp drop in the
rest-frame UV), it seems unlikely that very dusty objects (with
fesc << 1) would contribute in any significant manner
to the ionizing metagalactic flux.
As the hydrogen mean recombination timescale, 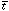 rec, at high
redshifts is much smaller than the then Hubble time
[34], it is
possible to compute
at any given epoch a critical value for the photon emission rate per unit
cosmological comoving volume,
rec, at high
redshifts is much smaller than the then Hubble time
[34], it is
possible to compute
at any given epoch a critical value for the photon emission rate per unit
cosmological comoving volume,
independently of the (unknown) previous emission history of the universe: only
rates above this value will provide enough UV photons to ionize the IGM by
that epoch. Here
It is interesting to convert the derived value of
(The conversion factor assumes a Salpeter IMF with solar metallicity). The
star-formation density given in
equation (9) is comparable with the value directly ``observed''
(i.e., uncorrected for dust reddening) at z
3 Note that, at
z = 3, Lyman-break galaxies would radiate
more ionizing photons than QSOs for fesc 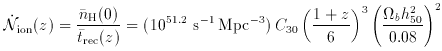
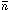 H(0)
is the mean hudrogen density of the
expanding IGM at the present-epoch, and C is the ionized hydrogen
clumping factor. One can then compare our determinations of
H(0)
is the mean hudrogen density of the
expanding IGM at the present-epoch, and C is the ionized hydrogen
clumping factor. One can then compare our determinations of
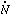 ion to
the estimated
contribution from QSOs and star-forming galaxies.
The uncertainty on this critical rate is difficult to estimate, as it depends
on the clumpiness of the IGM (scaled in the expression above
to the value inferred at z = 5 from numerical simulations
[18])
and the nucleosynthesis constrained baryon density. The
evolution of the critical rate as a function of redshift is plotted in
Figure 4. While
ion to
the estimated
contribution from QSOs and star-forming galaxies.
The uncertainty on this critical rate is difficult to estimate, as it depends
on the clumpiness of the IGM (scaled in the expression above
to the value inferred at z = 5 from numerical simulations
[18])
and the nucleosynthesis constrained baryon density. The
evolution of the critical rate as a function of redshift is plotted in
Figure 4. While 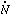 ion is
comparable to the quasar contribution at
z
ion is
comparable to the quasar contribution at
z  3, there is
some indication of a deficit of Lyman
continuum photons at z = 5. For bright, massive galaxies to
produce enough UV radiation at
z = 5, their space density would have to be comparable to the one
observed at z
3, there is
some indication of a deficit of Lyman
continuum photons at z = 5. For bright, massive galaxies to
produce enough UV radiation at
z = 5, their space density would have to be comparable to the one
observed at z  3, with
most ionizing photons being able to escape freely from the
regions of star formation into the IGM. This scenario may be in
conflict with direct observations of local starbursts below
the Lyman limit showing that at most a few percent of the stellar ionizing
radiation produced by these luminous sources actually escapes into the IGM
[30].
(3)
If, on the other
hand, faint QSOs with (say) MAB = -19 at rest-frame
ultraviolet frequencies
were to provide all the required ionizing flux, their
comoving space density would be such (0.0015 Mpc-3) that about 50
of them would expected in the HDF down to IAB = 27.2.
At z
3, with
most ionizing photons being able to escape freely from the
regions of star formation into the IGM. This scenario may be in
conflict with direct observations of local starbursts below
the Lyman limit showing that at most a few percent of the stellar ionizing
radiation produced by these luminous sources actually escapes into the IGM
[30].
(3)
If, on the other
hand, faint QSOs with (say) MAB = -19 at rest-frame
ultraviolet frequencies
were to provide all the required ionizing flux, their
comoving space density would be such (0.0015 Mpc-3) that about 50
of them would expected in the HDF down to IAB = 27.2.
At z  5, they
would appear very red in V - I as the Ly
5, they
would appear very red in V - I as the Ly forest is shifted into the visible.
This simple model can be ruled out, however, as there is only a handful (7)
of sources in the HDF with (V - I)AB > 1.5 mag down to
this magnitude limit.
forest is shifted into the visible.
This simple model can be ruled out, however, as there is only a handful (7)
of sources in the HDF with (V - I)AB > 1.5 mag down to
this magnitude limit.
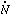 ion
into a ``minimum'' SFR per unit (comoving) volume,
ion
into a ``minimum'' SFR per unit (comoving) volume,  *
(hereafter we assume
*
(hereafter we assume  b h250 = 0.08 and
C = 30):
b h250 = 0.08 and
C = 30):
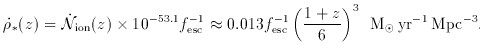 (9)
(9)
 3
[35].
3
[35].
2 At
all ages  0.1 Gyr one has
L(1500) / L(912)
0.1 Gyr one has
L(1500) / L(912)  6 for a Salpeter mass
function and constant SFR
[3]. This number
neglects any correction
for intrinsic HI absorption. Back.
6 for a Salpeter mass
function and constant SFR
[3]. This number
neglects any correction
for intrinsic HI absorption. Back.
 30%. Back.
30%. Back.