


When an isolated point source of ionizing radiation turns on, the ionized volume initially grows in size at a rate fixed by the emission of UV photons, and an ionization front separating the H II and H I regions propagates into the neutral gas. Most photons travel freely in the ionized bubble, and are absorbed in a transition layer. The evolution of an expanding H II region is governed by the equation
where VI is the proper
volume of the ionized zone,
One should point out that the
use of a volume-averaged clumping factor, C, in the recombination
timescale
is only justified when the size of the H II region is large compared to the
scale of the clumping, so that the effect of many clumps (filaments) within
the ionized volume can be averaged over (see
Figure 5).
Across the I-front the degree of
ionization changes sharply on a distance of the order of the mean free path of
an ionizing photon. When
In analogy with the individual H II region case, it can be shown that hydrogen
component in a highly inhomogeneous universe is completely reionized when the
number of photons emitted above 1 ryd in one recombination time equals the
mean number of hydrogen atoms
[39].
At any given epoch there is a
critical value for the photon emission rate per unit cosmological comoving
volume,
independently of the (unknown) previous emission history of the universe: only
rates above this value will provide enough UV photons to ionize the IGM by
that epoch. One can then compare our estimate of
Figure 5. Propagation of an ionization front in a
1283
cosmological density field produced by a mini-quasar with
It is interesting to convert the derived value of
The star formation density given in the equation above is comparable
with the value directly ``observed''
(i.e., uncorrected for dust reddening) at z
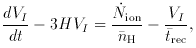
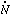 ion is the number of ionizing
photons emitted by the central source per unit time,
ion is the number of ionizing
photons emitted by the central source per unit time, 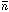 H is the
mean hydrogen density of the expanding IGM, H is the Hubble
constant, and
H is the
mean hydrogen density of the expanding IGM, H is the Hubble
constant, and
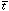 rec is
the hydrogen mean recombination timescale,
rec is
the hydrogen mean recombination timescale,
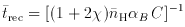
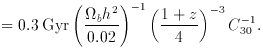
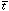 rec >> t, the growth of the H II
region is slowed down by recombinations in the highly inhomogeneous
medium, and its evolution
can be decoupled from the expansion of the universe. Just like in the static
case, the ionized bubble will fill its time-varying Strömgren sphere
after a few recombination timescales,
rec >> t, the growth of the H II
region is slowed down by recombinations in the highly inhomogeneous
medium, and its evolution
can be decoupled from the expansion of the universe. Just like in the static
case, the ionized bubble will fill its time-varying Strömgren sphere
after a few recombination timescales,
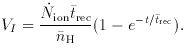
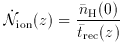
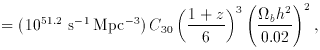
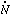 ion to the
estimated contribution from QSOs and star-forming galaxies.
The uncertainty on this critical rate is difficult to estimate, as it depends
on the clumpiness of the IGM (scaled in the expression above
to the value inferred at z = 5 from numerical simulations
[22])
and the nucleosynthesis constrained baryon density. The
evolution of the critical rate as a function of redshift is plotted in
Figure 4 (right). While
ion to the
estimated contribution from QSOs and star-forming galaxies.
The uncertainty on this critical rate is difficult to estimate, as it depends
on the clumpiness of the IGM (scaled in the expression above
to the value inferred at z = 5 from numerical simulations
[22])
and the nucleosynthesis constrained baryon density. The
evolution of the critical rate as a function of redshift is plotted in
Figure 4 (right). While  ion is
comparable to the quasar contribution at
z
ion is
comparable to the quasar contribution at
z  3, there is
some indication of a deficit of Lyman
continuum photons at z = 5. For bright, massive galaxies to
produce enough UV radiation at
z = 5, their space density would have to be comparable to the one
observed at
z
3, there is
some indication of a deficit of Lyman
continuum photons at z = 5. For bright, massive galaxies to
produce enough UV radiation at
z = 5, their space density would have to be comparable to the one
observed at
z  3, with most
ionizing photons being able to escape freely from the
regions of star formation into the IGM. This scenario may be in
conflict with direct observations of local starbursts below
the Lyman limit showing that at most a few percent of the stellar ionizing
radiation produced by these luminous sources actually escapes into the IGM
[34].
(4)
3, with most
ionizing photons being able to escape freely from the
regions of star formation into the IGM. This scenario may be in
conflict with direct observations of local starbursts below
the Lyman limit showing that at most a few percent of the stellar ionizing
radiation produced by these luminous sources actually escapes into the IGM
[34].
(4)
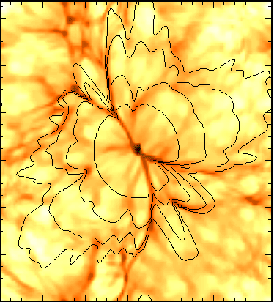
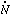 = 5 x
1053 s-1. The box length is 2.4 comoving Mpc. The
quasar is turned
on at the densest cell, which is found in a virialized halo of total mass
1.3 x 1011 M
= 5 x
1053 s-1. The box length is 2.4 comoving Mpc. The
quasar is turned
on at the densest cell, which is found in a virialized halo of total mass
1.3 x 1011 M .
The solid contours give the position of the I-front at 0.15, 0.25, 0.38, and
0.57 Myr after the quasar has switched on at z = 7. The
underlying greyscale image indicates the initial H I density field. (From
[1].)
.
The solid contours give the position of the I-front at 0.15, 0.25, 0.38, and
0.57 Myr after the quasar has switched on at z = 7. The
underlying greyscale image indicates the initial H I density field. (From
[1].)
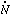 ion
into a ``minimum'' SFR per unit (comoving) volume,
ion
into a ``minimum'' SFR per unit (comoving) volume,  *
(hereafter we assume
*
(hereafter we assume  bh2 = 0.02 and C
= 30):
bh2 = 0.02 and C
= 30):
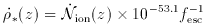
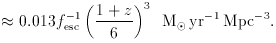
 3
[41].
The conversion factor assumes a Salpeter IMF with solar metallicity, and has
been computed using a population synthesis code
[6].
It can be understood by noting that, for each 1 M
3
[41].
The conversion factor assumes a Salpeter IMF with solar metallicity, and has
been computed using a population synthesis code
[6].
It can be understood by noting that, for each 1 M of stars formed,
8% goes into massive stars with M > 20 M
of stars formed,
8% goes into massive stars with M > 20 M that dominate the
Lyman continuum luminosity of a stellar population. At the end of the C-burning
phase, roughly half of the initial mass is converted into helium and carbon,
with a mass fraction released as radiation of 0.007. About 25% of the energy
radiated away goes
into ionizing photons of mean energy 20 eV. For each 1 M
that dominate the
Lyman continuum luminosity of a stellar population. At the end of the C-burning
phase, roughly half of the initial mass is converted into helium and carbon,
with a mass fraction released as radiation of 0.007. About 25% of the energy
radiated away goes
into ionizing photons of mean energy 20 eV. For each 1 M of stars
formed every year, we then expect
of stars
formed every year, we then expect
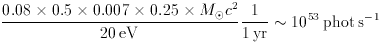
4 Note that, at z = 3, Lyman-break galaxies
would radiate
more ionizing photons than QSOs for fesc  30%. Back.
30%. Back.