


With the help of some simple stellar population synthesis tools we can now
set a lower limit to the total stellar mass density
that produced the observed sky brightness and constrain
the cosmic history of star birth in galaxies. One of the most serious
uncertainties in this calculation has always been the lower cutoff
(usually treated as a free parameter) of the
initial mass function (IMF).
Observations of M subdwarfs stars with the HST have recently
shed some light on this issue, showing that the IMF in the Galactic disk can
be represented analytically
over the mass range 0.1 <m < 1.6 (here m is in solar
units) by log  (m) = const -
2.33 log m - 1.82(log
m)2
([17], hereafter
GBF). For m > 1 this mass distribution agrees well with a
Salpeter function. Observations of normal Galactic
star-forming regions also show some convergence in the basic form of the
IMF at intermediate and high
masses, a power-law slope that is consistent with the Salpeter value
[13].
In the following I will use a ``universal'' IMF with the
GBF form for m < 1, matched to a Salpeter slope for m
(m) = const -
2.33 log m - 1.82(log
m)2
([17], hereafter
GBF). For m > 1 this mass distribution agrees well with a
Salpeter function. Observations of normal Galactic
star-forming regions also show some convergence in the basic form of the
IMF at intermediate and high
masses, a power-law slope that is consistent with the Salpeter value
[13].
In the following I will use a ``universal'' IMF with the
GBF form for m < 1, matched to a Salpeter slope for m
 1; the mass integral of this
function is 0.6 times that obtained extrapolating a Salpeter function down to
0.1 M
1; the mass integral of this
function is 0.6 times that obtained extrapolating a Salpeter function down to
0.1 M . (1)
. (1)
|
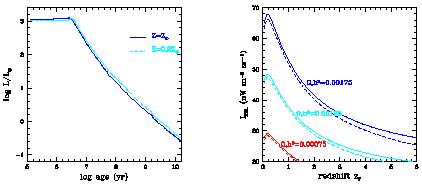
Figure 4. Left: Synthetic
[4]
bolometric luminosity versus age of a simple stellar
population having total mass M = 1
M |
As shown in Figure 4, the bolometric
luminosity as a function of age  of
a simple stellar population (a single generation of coeval,
chemically homogeneous stars having total mass M, solar
metallicity, and the above IMF) can be well approximated by
of
a simple stellar population (a single generation of coeval,
chemically homogeneous stars having total mass M, solar
metallicity, and the above IMF) can be well approximated by
(cf [6]).
Over a timescale of 13 Gyr (the age of the universe for an EdS cosmology with
h = 0.5), about 1.3 MeV per stellar baryon are radiated
away. This number
depends only weakly on the assumed metallicity of stars.
In a stellar system with arbitrary star formation rate per comoving
cosmological volume,
The total background light observed at Earth (t =
tH) is
where the factor (1 + z) at the denominator is lost to cosmic expansion
when converting from observed to radiated (comoving) luminosity density.
To set a lower limit to the present-day mass density,
A visible mass density at the level of the above lower limit,
0.00125h-2 I50,
while able to explain the measured sky brightness, requires all the stars that
give origin to the observed light to have formed at zF
This model fits reasonably well all
measurements of the UV-continuum and H
The observed EBL therefore requires that between 7% and 16%
of the nucleosynthetic baryons are today in the forms of stars,
processed gas, and their remnants.
According to the most recent census of cosmic baryons, the mass density in
stars and their remnants observed today is
1 The bolometric light contributed by
stars less massive than 1
M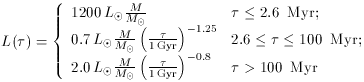
 *, and formation epoch
tF, the comoving bolometric emissivity
at time t is given by the convolution integral
*, and formation epoch
tF, the comoving bolometric emissivity
at time t is given by the convolution integral
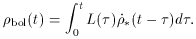
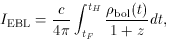
 *, of
processed gas + stars
(in units of the critical density
*, of
processed gas + stars
(in units of the critical density  crit = 2.77 x 1011
h2 M
crit = 2.77 x 1011
h2 M Mpc-3), consider now a scenario where all stars
are formed instantaneously at redshift zF.
The background light that would be observed at Earth from such an event
is shown in Figure 4 as a function of
zF for
Mpc-3), consider now a scenario where all stars
are formed instantaneously at redshift zF.
The background light that would be observed at Earth from such an event
is shown in Figure 4 as a function of
zF for  * h2 = 0.00075,
0.00125, 0.00175 (corresponding to 9, 6.5, and 4 percent of the
nucleosynthetic baryon density,
* h2 = 0.00075,
0.00125, 0.00175 (corresponding to 9, 6.5, and 4 percent of the
nucleosynthetic baryon density,
 b
h2 = 0.0193 ± 0.0014
[5]),
and two different cosmologies. A couple of points are
worth noting here: (1) the time evolution of the luminosity radiated by a
simple stellar population makes
the dependence of the observed EBL from zF much
shallower than the (1 + zF)-1
lost to cosmic expansion, as the energy output from
stars is spread over their respective lifetimes; and (2) in order to generate
an EBL at a level of 50 I50 n W m-2
sr-1, one requires
b
h2 = 0.0193 ± 0.0014
[5]),
and two different cosmologies. A couple of points are
worth noting here: (1) the time evolution of the luminosity radiated by a
simple stellar population makes
the dependence of the observed EBL from zF much
shallower than the (1 + zF)-1
lost to cosmic expansion, as the energy output from
stars is spread over their respective lifetimes; and (2) in order to generate
an EBL at a level of 50 I50 n W m-2
sr-1, one requires
 *
h2 > 0.00125 I50 (for an EdS
universe with h = 0.5), hence a mean
mass-to-blue light ratio today of < M / LB
>* > 3.5 I50
for a present-day blue luminosity density of
*
h2 > 0.00125 I50 (for an EdS
universe with h = 0.5), hence a mean
mass-to-blue light ratio today of < M / LB
>* > 3.5 I50
for a present-day blue luminosity density of
 B =
2.0 x 108 h L
B =
2.0 x 108 h L Mpc-3
[11].
As shown in Figure 4, the dependence of these
estimates on the
cosmological model is rather weak.
With the adopted IMF, about 30% of this mass will be returned to
the interstellar medium in 108 yr after intermediate-mass
stars eject
their envelopes and massive stars explode as supernovae. This ``return
fraction'',
R, becomes 50% after about 10 Gyr.
Mpc-3
[11].
As shown in Figure 4, the dependence of these
estimates on the
cosmological model is rather weak.
With the adopted IMF, about 30% of this mass will be returned to
the interstellar medium in 108 yr after intermediate-mass
stars eject
their envelopes and massive stars explode as supernovae. This ``return
fraction'',
R, becomes 50% after about 10 Gyr.
 0.2, and is,
as such, rather implausible.
A more realistic
scenario appears to be one where the star formation density evolves as
0.2, and is,
as such, rather implausible.
A more realistic
scenario appears to be one where the star formation density evolves as
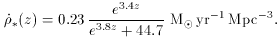
 luminosity densities
from the present-epoch to z = 4 after an extinction correction of
A1500 = 1.2 mag (A2800 = 0.55 mag)
is applied to the data
[21],
and produce a total EBL of the right magnitude (I50 = 1).
Since about half of the present-day stars are formed at z > 1.3
(hence their contribution to the EBL is redshifted away),
the resulting visible mass density is
luminosity densities
from the present-epoch to z = 4 after an extinction correction of
A1500 = 1.2 mag (A2800 = 0.55 mag)
is applied to the data
[21],
and produce a total EBL of the right magnitude (I50 = 1).
Since about half of the present-day stars are formed at z > 1.3
(hence their contribution to the EBL is redshifted away),
the resulting visible mass density is  * h2 = 0.0031
I50 (< M / LB >* = 8.6
I50). Note that this estimate ignores the recycling
of returned gas into new stars.
* h2 = 0.0031
I50 (< M / LB >* = 8.6
I50). Note that this estimate ignores the recycling
of returned gas into new stars.
 s h =
0.00245+0.00125-0.00088
[16],
corresponding to a mean visible mass-to-blue light
ratio of < M / LB >s =
3.4+1.7-1.3 (h = 0.5) (about 70% of
this mass is found in old spheroidal populations). While this is about a
factor of 2.5 smaller than the visible mass density predicted by equation
(7), efficient recycling of ejected material into new star
formation would tend to reduce the apparent discrepancy in the budget.
Alternatively, the gas returned by stars may be ejected into the intergalactic
medium. With an IMF-averaged yield of returned metals of y
s h =
0.00245+0.00125-0.00088
[16],
corresponding to a mean visible mass-to-blue light
ratio of < M / LB >s =
3.4+1.7-1.3 (h = 0.5) (about 70% of
this mass is found in old spheroidal populations). While this is about a
factor of 2.5 smaller than the visible mass density predicted by equation
(7), efficient recycling of ejected material into new star
formation would tend to reduce the apparent discrepancy in the budget.
Alternatively, the gas returned by stars may be ejected into the intergalactic
medium. With an IMF-averaged yield of returned metals of y
 1.5
Z
1.5
Z ,
(2)
the predicted mean metallicity at the present epoch is
y
,
(2)
the predicted mean metallicity at the present epoch is
y  * /
* /
 b = 0.25
Z
b = 0.25
Z , in good
agreement with the values inferred from cluster abundances
[26].
, in good
agreement with the values inferred from cluster abundances
[26].
 is quite
small for a ``typical'' IMF. The use of the
GBF mass function at low masses instead of Salpeter leaves then the total
radiated luminosity of the stellar population virtually unaffected.
Back.
is quite
small for a ``typical'' IMF. The use of the
GBF mass function at low masses instead of Salpeter leaves then the total
radiated luminosity of the stellar population virtually unaffected.
Back.
2 Here we have taken y

 mpzm
mpzm  (m)dm
x [
(m)dm
x [ m
m  (m)dm]-1, the stellar yields
pzm of
[33],
and a GBF + Salpeter IMF. Back.
(m)dm]-1, the stellar yields
pzm of
[33],
and a GBF + Salpeter IMF. Back.