


1.3. Gunn-Peterson Effect
Consider radiation emitted at some frequency
 e that lies blueward of
Ly
e that lies blueward of
Ly by a source at redshift
ze, and observed at Earth at frequency
by a source at redshift
ze, and observed at Earth at frequency
 o =
o =
 e (1 +
ze)-1. At a redshift z such that
(1 + z) = (1 + ze)
e (1 +
ze)-1. At a redshift z such that
(1 + z) = (1 + ze)

 /
/
 e, the emitted photons
pass through the local
Ly
e, the emitted photons
pass through the local
Ly resonance as they propagates
towards us through a smoothly distributed sea of neutral hydrogen atoms,
and are scattered off the line-of-sight with a cross-section
(neglecting stimulated emission) of
resonance as they propagates
towards us through a smoothly distributed sea of neutral hydrogen atoms,
and are scattered off the line-of-sight with a cross-section
(neglecting stimulated emission) of
where f = 0.4162 is the upward oscillator strength for the
transition,
where dl /dz = c H0-1 (1 + z)-1
[
In an Einstein-de Sitter
(
The same
expression for the opacity is also valid in the case of optically thin (to
Ly
In an expanding Universe homogeneously filled with neutral hydrogen,
the above equations
apply to all parts of the source spectrum to the blue of
Ly
In modern interpretations of the IGM, it is difficult to use the Gunn-Peterson
effect to quantify the amount of ionizing radiation that is necessary to keep
the neutral hydrogen absorption below the detection limits. This is because,
in hierarchical clustering scenarios for the formation of cosmic structures
(the Cold Dark Matter model being the most studied example), the
accumulation of matter in overdense regions under the influence of gravity
reduces the optical depth for Ly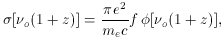
 is the line profile
function [with normalization
is the line profile
function [with normalization

 (
( )
d
)
d = 1], c is the speed
of light,
and e and me are the electron charge and mass,
respectively.
The total optical depth for resonant scattering at the observed frequency is
given by the line integral of this cross-section times the neutral
hydrogen proper density nHI(z),
= 1], c is the speed
of light,
and e and me are the electron charge and mass,
respectively.
The total optical depth for resonant scattering at the observed frequency is
given by the line integral of this cross-section times the neutral
hydrogen proper density nHI(z),
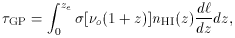
 M (1 +
z)3 +
M (1 +
z)3 +
 K (1 +
z)2 +
K (1 +
z)2 +

 ]-1/2 is the
proper line element in a Friedmann-Robertson-Walker metric, and
]-1/2 is the
proper line element in a Friedmann-Robertson-Walker metric, and
 M,
M,

 , and
, and
 K = 1 -
K = 1 -
 M -
M -

 are the matter, vacuum, and curvature contribution to
the present density parameter.
As the scattering cross-section is sharply peaked around
are the matter, vacuum, and curvature contribution to
the present density parameter.
As the scattering cross-section is sharply peaked around

 , we can write
, we can write
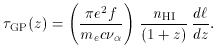
 M = 1,
M = 1,

 = 0) Universe, this
becomes
= 0) Universe, this
becomes
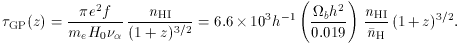
 scattering) discrete clouds
as long as nHI is replaced with
the average neutral density of individual clouds times their volume filling
factor.
scattering) discrete clouds
as long as nHI is replaced with
the average neutral density of individual clouds times their volume filling
factor.
 . An absorption
trough should then be detected in the level of the rest-frame
UV continuum of the quasar; this is the so-called ``Gunn-Peterson effect''.
Between the discrete absorption lines of the
Ly
. An absorption
trough should then be detected in the level of the rest-frame
UV continuum of the quasar; this is the so-called ``Gunn-Peterson effect''.
Between the discrete absorption lines of the
Ly forest clouds, quasar spectra do not show a pronounced Gunn-Peterson
absorption trough. The current upper limit at ze
forest clouds, quasar spectra do not show a pronounced Gunn-Peterson
absorption trough. The current upper limit at ze
 5 is
5 is
 GP < 0.1 in
the region of minimum opacity, implying from equation (14) a neutral
fraction of nHI /
GP < 0.1 in
the region of minimum opacity, implying from equation (14) a neutral
fraction of nHI /
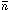 H < 10-6
h. Even if 99% of all the cosmic
baryons fragment at these epochs into structures that can be identified with
quasar absorption systems, with only 1% remaining in a smoothly distributed
component, the implication is a diffuse IGM which is
ionized to better than 1 part in 104.
H < 10-6
h. Even if 99% of all the cosmic
baryons fragment at these epochs into structures that can be identified with
quasar absorption systems, with only 1% remaining in a smoothly distributed
component, the implication is a diffuse IGM which is
ionized to better than 1 part in 104.
 scattering considerably below the average
in most of the volume of the Universe, and regions of minimum opacity occur
in the most underdense areas (expanding `cosmic minivoids').
scattering considerably below the average
in most of the volume of the Universe, and regions of minimum opacity occur
in the most underdense areas (expanding `cosmic minivoids').