


2.1. Distribution of Column Densities and Evolution
The bivariate distribution f(NHI, z) of H I column densities and redshifts is defined by the probability dP that a line-of-sight intersects a cloud with column density NHI in the range dNHI, at redshift z in the range dz,
As a function of column, a single power-law with slope -1.5 appears to
provide at high redshift a surprisingly good description over 9
decades in NHI, i.e. from 1012 to
1021 cm-2.
It is a reasonable approximation to use for the distribution
of absorbers along the line-of-sight:
Ly
A normalization value of A = 4.0 x 107 produces then ~
3 LLS per
unit redshift at z = 3, and, at the same epoch, ~ 150 forest
lines above NHI = 1013.8 cm-2,
in reasonable agreement with the observations.
If absorbers at a given surface density are conserved, with fixed comoving
space number density n = n0 (1 +
z)3 and geometric cross-section
If the Universe is cosmologically flat, the expansion rate at early epochs
is close to the Einstein-de Sitter limit, and the redshift distribution
for conserved clouds is predicted to be
The rate of increase of f(NHI, z) with
z in both the Ly
For clouds with NHI > 1014 cm-2,
this amounts to L ~ 0.7 h-1
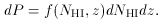
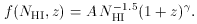
 forest clouds and
Lyman-limit systems appear to evolve at slightly different rates, with
forest clouds and
Lyman-limit systems appear to evolve at slightly different rates, with
 = 1.5 ± 0.4
for the LLS and
= 1.5 ± 0.4
for the LLS and
 = 2.8 ± 0.7
for the forest lines. Let us assume, for simplicity, a single redshift
exponent,
= 2.8 ± 0.7
for the forest lines. Let us assume, for simplicity, a single redshift
exponent,
 = 2, for the
entire range in
column densities. In the power-law model (16) the number N of
absorbers with columns greater than NHI per unit
increment of redshift is
= 2, for the
entire range in
column densities. In the power-law model (16) the number N of
absorbers with columns greater than NHI per unit
increment of redshift is
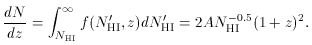
 , then
the intersection probability per unit redshift interval is
, then
the intersection probability per unit redshift interval is
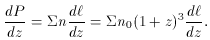
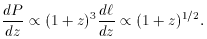
 forest and LLS
is considerably faster than this, indicating rapid
evolution. The mean proper distance between absorbers along the line-of-sight
with columns greater than NHI is
forest and LLS
is considerably faster than this, indicating rapid
evolution. The mean proper distance between absorbers along the line-of-sight
with columns greater than NHI is
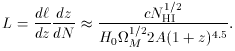
 M-1/2 Mpc
at z = 3. At the same epoch, the mean proper distance
between LLS is L ~ 30 h-1
M-1/2 Mpc
at z = 3. At the same epoch, the mean proper distance
between LLS is L ~ 30 h-1
 M-1/2 Mpc.
M-1/2 Mpc.