2. BASIC RADIATIVE TRANSFER

There are numerous textbooks which derive the basic radiative transfer equations for the 21-cm line of neutral hydrogen, mostly following Wild (1952). For the sake of completeness and to avoid ambiguities due to a different choice of notation I will summarize the most significant formulae involved, following the notation used by Kulkarni and Heiles (1988).

The starting point is the equation of radiative transfer:

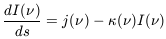
(1)

where I() is the specific intensity at frequency , j() the emissivity, () the absorption coefficient and s the distance along the line of sight. Let us introduce the usual definitions for the optical depth d() = ()ds and for the source function S() = j() / (). In thermodynamic equilibrium Kirchoff's law applies so that, using the Rayleigh-Jeans approximation for the Planck law, the source function at radio wavelengths can be written as:

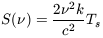
(2)

Here c is the speed of light in vacuum, k Boltzmann's constant and T_s the spin temperature. In an equivalent way one can define a brightness temperature T_B which corresponds to the temperature which a black body would have at frequency if it were to emit the specific intensity I(). Now we can rewrite the equation of transfer as:

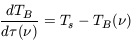
(3)

This equation can be solved in the case of a homogeneous isolated HI cloud embedded in a background radiation field with a brightness temperature of T_bg. Employing e as an integrating factor one finds the following important relation:

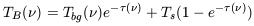
(4)

Let us assume that one can ignore the background radiation (T_bg << T_s). In the case of an optically thick cloud (() >> 1) the formula for the brightness temperature simply reduces to T_B = T_s, or the measured brightness temperature is equal to the spin temperature, or characteristic temperature, of the cloud. If the cloud is optically thin (() << 1) we find that T_B = ()T_s. It is important to realize that () is directly related to the absorption coefficient per H atom which is dependent on atomic constants only. Then

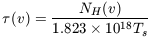
(5)

In this relation N_H is defined as the column density of HI along the line of sight in atoms cm^-2 and the dependence on frequency has been changed for dependence on velocity, expressed in km s^-1. In general the profile of the HI line is determined by its Doppler width which in turn is dominated by the macroscopic motion of the gas. Combining all this, we find in the optically thin case the following useful relation:

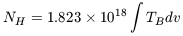
(6)

When reporting HI column densities and HI masses based on this formula, radio astronomers implicitly assume that the emission comes from an optically thin medium. However, HI absorption studies of the Galaxy have indicated that an appreciable fraction of the gas is optically thick so that column densities derived under the assumption of << 1 represent a lower limit to the true HI content.

Now let us look at what happens when T_bg > T_s. In general an HI spectrum is measured with respect to the background emission,

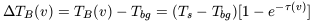
(7)

If there is a strong background source present a spectrum along the line of sight towards this source will show an absorption feature. By measuring a spectrum along a nearby line of sight which presumably has an identical emission spectrum, and assuming that the brightness temperature, T_src of the source has been determined separately, one can determine the optical depth profile

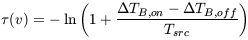
(8)

Once the optical depth profile is known the spin temperature can be derived directly via T_s(v) = T_B,off / (1 - e^-(v)). As explained in Kulkari and Heiles the spin temperature is in general a column-density weighted harmonic-mean temperature. Therefore, and to enable a meaningful comparison between different regions in the Galaxy, a better parameter is the integrated optical depth which was introduced by Crovisier (1981) and which is defined as:

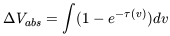
(9)

Correspondingly one can define the mean spin temperature as:

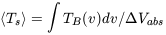
(10)

In the case that the spin temperature would drop as low as the 2.7 K cosmic background temperature, no HI emission could be observed above the background and clouds such as the giant HI ring in Leo detected by Schneider et al. (1983), but with even lower densities, could go unobserved. However, it seems that this situation is unlikely as pointed out by Schneider et al. (1989) for the M96 group and by Corbelli and Salpeter (1990), who report on an extensive HI absorption line survey of High Velocity Clouds (HVCs) and a study of HI absorption towards bright extragalactic sources whose lines of sight pass close to galaxies. They find no evidence for HI column densities of about 5 × 10¹⁸ atoms cm^-2 or larger which are hidden from detection in emission because their spin temperature approaches the microwave background temperature (the subthermal HI effect). Secondly, they infer from their data a lower limit for T_s of several hundred Kelvin for clouds with column densities of the order of 10²⁰ atoms cm^-2 with some evidence for cold HI being present in directions with larger column densities (cf. the review by J. Kenney in this volume for more information on this subject).