2. COSMOLOGICAL STRUCTURE FORMATION

The Big Bang theory is built upon the Cosmological Principle, a symmetry principle that requires the Universe on large scales to be both homogeneous and isotropic. Space-times consistent with this requirement can be described by the Robertson-Walker metric

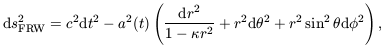
(1)

where is the spatial curvature, scaled so as to take the values 0 or ± 1. The case = 0 represents flat space sections, and the other two cases are space sections of constant positive or negative curvature, respectively. The time coordinate t is called cosmological proper time and it is singled out as a preferred time coordinate by the property of spatial homogeneity. The quantity a(t), the cosmic scale factor, describes the overall expansion of the universe as a function of time. If light emitted at time t_e is received by an observer at t₀ then the redshift z of the source is given by

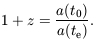
(2)

The dynamics of an FRW universe are determined by the Einstein gravitational field equations which become

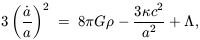
	(3)
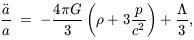
	(4)
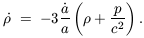
	(5)

These equations determine the time evolution of the cosmic scale factor a(t) (the dots denote derivatives with respect to cosmological proper time t) and therefore describe the global expansion or contraction of the universe. The behaviour of these models can further be parametrised in terms of the Hubble parameter H = / a and the density parameter = 8 G / 3H², a suffix 0 representing the value of these quantities at the present epoch when t = t₀.

2.2. Linear Perturbation Theory

In order to understand how structures form we need to consider the difficult problem of dealing with the evolution of inhomogeneities in the expanding Universe. We are helped in this task by the fact that we expect such inhomogeneities to be of very small amplitude early on so we can adopt a kind of perturbative approach, at least for the early stages of the problem. If the length scale of the perturbations is smaller than the effective cosmological horizon d_H = c / H₀, a Newtonian treatment of the subject is expected to be valid. If the mean free path of a particle is small, matter can be treated as an ideal fluid and the Newtonian equations governing the motion of gravitating particles in an expanding universe can be written in terms of x = r / a(t) (the comoving spatial coordinate, which is fixed for observers moving with the Hubble expansion), v = 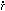- Hr = a 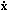(the peculiar velocity field, representing departures of the matter motion from pure Hubble expansion), (x, t) (the peculiar Newtonian gravitational potential, i.e. the fluctuations in potential with respect to the homogeneous background) and (x, t) (the matter density). Using these variables we obtain, first, the Euler equation:

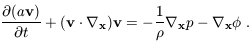
(6)

The second term on the right-hand side of equation (6) is the peculiar gravitational force, which can be written in terms of g = - _x / a, the peculiar gravitational acceleration of the fluid element. If the velocity flow is irrotational, v can be rewritten in terms of a velocity potential _v: v = - _{x v} / a. Next we have the continuity equation:

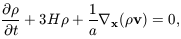
(7)

which expresses the conservation of matter, and finally the Poisson equation:

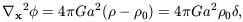
(8)

describing Newtonian gravity. Here ₀ is the mean background density, and

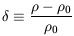
(9)

is the density contrast.

The next step is to linearise the Euler, continuity and Poisson equations by perturbing physical quantities defined as functions of Eulerian coordinates, i.e. relative to an unperturbed coordinate system. Expanding , v and perturbatively and keeping only the first-order terms in equations (6) and (7) gives the linearised continuity equation:

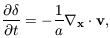
(10)

which can be inverted, with a suitable choice of boundary conditions, to yield

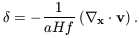
(11)

The function f ₀^0.6; this is simply a fitting formula to the full solution [Peebles 1980]. The linearised Euler and Poisson equations are

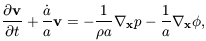
	(12)
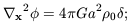
	(13)

|v|, ||, || << 1 in equations (11), (12) & (13). From these equations, and if one ignores pressure forces, it is easy to obtain an equation for the evolution of :

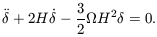
(14)

For a spatially flat universe dominated by pressureless matter, ₀(t) = 1 / 6 Gt² and equation (14) admits two linearly independent power law solutions (x, t) = D_±(t) (x), where D₊(t) a(t) t^2/3 is the growing mode and D_-(t) t^-1 is the decaying mode.

2.3. Primordial density fluctuations

The above considerations apply to the evolution of a single Fourier mode of the density field (x, t) = D₊(t) (x). What is more likely to be relevant, however, is the case of a superposition of waves, resulting from some kind of stochastic process in which he density field consists of a superposition of such modes with different amplitudes. A statistical description of the initial perturbations is therefore required, and any comparison between theory and observations will also have to be statistical.

The spatial Fourier transform of (x) is

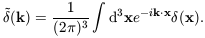
(15)

It is useful to specify the properties of in terms of . We can define the power-spectrum of the field to be (essentially) the variance of the amplitudes at a given value of k:

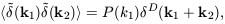
(16)

where ^D is the Dirac delta function; this rather cumbersome definition takes account of the translation symmetry and reality requirements for P(k); isotropy is expressed by P(k) = P(k). The analogous quantity in real space is called the two-point correlation function or, more correctly, the autocovariance function, of (x):

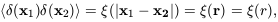
(17)

which is itself related to the power spectrum via a Fourier transform. The shape of the initial fluctuation spectrum, is assumed to be imprinted on the universe at some arbitrarily early time. Many versions of the inflationary scenario for the very early universe [Guth 1981, Guth & Pi 1982] produce a power-law form

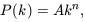
(18)

with a preference in some cases for the Harrison-Zel'dovich form with n = 1 [Harrison 1970, Zel'dovich 1972]. Even if inflation is not the origin of density fluctuations, the form (18) is a useful phenomenological model for the fluctuation spectrum. These considerations specify the shape of the fluctuation spectrum, but not its amplitude. The discovery of temperature fluctuations in the CMB [Smoot et al. 1992] has plugged that gap.

The power-spectrum is particularly important because it provides a complete statistical characterisation of a particular kind of stochastic process: a Gaussian random field. This class of field is the generic prediction of inflationary models, in which the density perturbations are generated by Gaussian quantum fluctuations in a scalar field during the inflationary epoch [Guth & Pi 1982, Brandenberger 1985].

2.4. The transfer function

We have hitherto assumed that the effects of pressure and other astrophysical processes on the gravitational evolution of perturbations are negligible. In fact, depending on the form of any dark matter, and the parameters of the background cosmology, the growth of perturbations on particular length scales can be suppressed relative to the growth laws discussed above.

We need first to specify the fluctuation mode. In cosmology, the two relevant alternatives are adiabatic and isocurvature. The former involve coupled fluctuations in the matter and radiation component in such a way that the entropy does not vary spatially; the latter have zero net fluctuation in the energy density and involve entropy fluctuations. Adiabatic fluctuations are the generic prediction from inflation and form the basis of most currently fashionable models, although interesting work has been done recently on isocurvature models [Peebles 1999a, Peebles 1999b].

In the classical Jeans instability, pressure inhibits the growth of structure on scales smaller than the distance traversed by an acoustic wave during the free-fall collapse time of a perturbation. If there are collisionless particles of hot dark matter, they can travel rapidly through the background and this free streaming can damp away perturbations completely. Radiation and relativistic particles may also cause kinematic suppression of growth. The imperfect coupling of photons and baryons can also cause dissipation of perturbations in the baryonic component. The net effect of these processes, for the case of statistically homogeneous initial Gaussian fluctuations, is to change the shape of the original power-spectrum in a manner described by a simple function of wave-number - the transfer function T(k) - which relates the processed power-spectrum P(k) to its primordial form P₀(k) via P(k) = P₀(k) × T²(k). The results of full numerical calculations of all the physical processes we have discussed can be encoded in the transfer function of a particular model [Bardeen et al. 1986]. For example, fast moving or `hot' dark matter particles (HDM) erase structure on small scales by the free-streaming effects mentioned above so that T(k) -> 0 exponentially for large k; slow moving or `cold' dark matter (CDM) does not suffer such strong dissipation, but there is a kinematic suppression of growth on small scales (to be more precise, on scales less than the horizon size at matter-radiation equality); significant small-scale power nevertheless survives in the latter case. These two alternatives thus furnish two very different scenarios for the late stages of structure formation: the `top-down' picture exemplified by HDM first produces superclusters, which subsequently fragment to form galaxies; CDM is a `bottom-up' model because small-scale structures form first and then merge to form larger ones. The general picture that emerges is that, while the amplitude of each Fourier mode remains small, i.e. (k) << 1, linear theory applies. In this regime, each Fourier mode evolves independently and the power-spectrum therefore just scales as

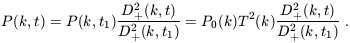
(19)

For scales larger than the Jeans length, this means that the shape of the power-spectrum is preserved during linear evolution.

2.5. Beyond linear theory

The linearised equations of motion provide an excellent description of gravitational instability at very early times when density fluctuations are still small ( << 1). The linear regime of gravitational instability breaks down when becomes comparable to unity, marking the commencement of the quasi-linear (or weakly non-linear) regime. During this regime the density contrast may remain small ( < 1), but the phases of the Fourier components _k become substantially different from their initial values resulting in the gradual development of a non-Gaussian distribution function if the primordial density field was Gaussian. In this regime the shape of the power-spectrum changes by virtue of a complicated cross-talk between different wave-modes. Analytic methods are available for this kind of problem [Sahni & Coles 1985], but the usual approach is to use N-body experiments for strongly non-linear analyses [Davis et al. 1985, Jenkins et al. 1999].

Further into the non-linear regime, bound structures form. The baryonic content of these objects may then become important dynamically: hydrodynamical effects (e.g. shocks), star formation and heating and cooling of gas all come into play. The spatial distribution of galaxies may therefore be very different from the distribution of the (dark) matter, even on large scales. Attempts are only just being made to model some of these processes with cosmological hydrodynamics codes [Cen 1992], but it is some measure of the difficulty of understanding the formation of galaxies and clusters that most studies have only just begun to attempt to include modelling the detailed physics of galaxy formation. In the front rank of theoretical efforts in this area are the so-called semi-analytical models which encode simple rules for the formation of stars within a framework of merger trees that allows the hierarchical nature of gravitational instability to be explicitly taken into account [Baugh et al. 1998].

The usual approach is instead simply to assume that the point-like distribution of galaxies, galaxy clusters or whatever,

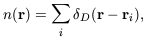
(20)

bears a simple functional relationship to the underlying (r). An assumption often invoked is that relative fluctuations in the object number counts and matter density fluctuations are proportional to each other, at least within sufficiently large volumes, according to the linear biasing prescription:

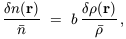
(21)

where b is what is usually called the biasing parameter. Alternatives, which are not equivalent, include the high-peak model ([Kaiser 1984, Bardeen et al. 1986]) and the various local bias models [Coles 1993]. Non-local biases are possible, but it is rather harder to construct such models [Bower et al. 1993]. If one is prepared to accept an ansatz of the form (21) then one can use linear theory on large scales to relate galaxy clustering statistics to those of the density fluctuations, e.g.

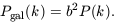
(22)

This approach is the one most frequently adopted in practice, but the community is becoming increasingly aware of its severe limitations. A simple parametrisation of this kind simply cannot hope to describe realistically the relationship between galaxy formation and environment [Dekel & Lahav 1999]. I will return to this question in Section 5.

2.6. Models of structure formation

It should now be clear that models of structure formation involve many ingredients which interact in a complicated way. In the following list, notice that most of these ingredients involve at least one assumption that may well turn out not to be true:

1. A background cosmology. This basically means a choice of ₀, H₀ and , assuming we are prepared to stick with the Robertson-Walker metric (1) and the Einstein equations (3)-(5).

2. An initial fluctuation spectrum. This is usually taken to be a power-law, but may not be. The most common choice is n = 1.

3. A choice of fluctuation mode: usually adiabatic.

4. A statistical distribution of fluctuations. This is often assumed to be Gaussian.

5. The transfer function, which requires knowledge of the relevant proportions of `hot', `cold' and baryonic material as well as the number of relativistic particle species.

6. A `machine' for handling non-linear evolution, so that the distribution of galaxies and other structures can be predicted. This could be an N-body or hydrodynamical code, an approximated dynamical calculation or simply, with fingers crossed, linear theory.

7. A prescription for relating fluctuations in mass to fluctuations in light, frequently the linear bias model.

Historically speaking, the first model incorporating non-baryonic dark matter to be seriously considered was the hot dark matter (HDM) scenario, in which the universe is dominated by a massive neutrino with mass around 10-30 eV. This scenario has fallen into disrepute because the copious free streaming it produces smooths the matter fluctuations on small scales and means that galaxies form very late. The favoured alternative for most of the 1980s was the cold dark matter (CDM) model in which the dark matter particles undergo negligible free streaming owing to their higher mass or non-thermal behaviour. A `standard' CDM model (SCDM) then emerged in which the cosmological parameters were fixed at ₀ = 1 and h = 0.5, the spectrum was of the Harrison-Zel'dovich form with n = 1 and a significant bias, b = 1.5 to 2.5, was required to fit the observations [Davis et al. 1985].

The SCDM model was ruled out by a combination of the COBE-inferred amplitude of primordial density fluctuations, galaxy clustering power-spectrum estimates on large scales, cluster abundances and small-scale velocity dispersions [Peacock & Dodds 1996]. It seems the standard version of this theory simply has a transfer function with the wrong shape to accommodate all the available data with an n = 1 initial spectrum. Nevertheless, because CDM is such a successful first approximation and seems to have gone a long way to providing an answer to the puzzle of structure formation, the response of the community has not been to abandon it entirely, but to seek ways of relaxing the constituent assumptions in order to get a better agreement with observations. Various possibilities have been suggested.

If the total density is reduced to ₀ 0.3, which is favoured by many arguments, then the size of the horizon at matter-radiation equivalence increases compared with SCDM and much more large-scale clustering is generated. . This is called the open cold dark matter model, or OCDM for short. Those unwilling to dispense with the inflationary predeliction for flat spatial sections have invoked ₀ = 0.2 and a positive cosmological constant [Efstathiou et al. 1990] to ensure that k = 0; this can be called CDM and is apparently also favoured by observations of distant supernovae [Perlmutter et al. 1999]. Much the same effect on the power spectrum may also be obtained in = 1 CDM models if matter-radiation equivalence is delayed, such as by the addition of an additional relativistic particle species. The resulting models are usually called CDM [White et al. 1995].

Another alternative to SCDM involves a mixture of hot and cold dark matter (CHDM), having perhaps _hot = 0.3 for the fractional density contributed by the hot particles. For a fixed large-scale normalisation, adding a hot component has the effect of suppressing the power-spectrum amplitude at small wavelengths [Klypin et al. 1993]. A variation on this theme would be to invoke a `volatile' rather than `hot' component of matter produced by the decay of a heavier particle [Pierpaoli et al. 1996]. The non-thermal character of the decay products results in subtle differences in the shape of the transfer function in the (CVDM) model compared to the CHDM version. Another possibility is to invoke non-flat initial fluctuation spectra, while keeping everything else in SCDM fixed. The resulting `tilted' models, TCDM, usually have n < 1 power-law spectra for extra large-scale power and, perhaps, a significant fraction of tensor perturbations [Lidsey & Coles 1992]. Models have also been constructed in which non-power-law behaviour is invoked to produce the required extra power: these are the broken scale-invariance (BSI) models [Gottlöber et al. 1994].

But diverse though this collection of alternative models may seem, it does not include models where the assumption of Gaussian statistics is relaxed. This is at least as important as the other ingredients which have been varied in some of the above models. The reason for this is that fully-specified non-Gaussian models are hard to construct, even if they are based on purely phenomenological considerations [Weinberg & Cole 1992, Coles et al. 1993]. Models based on topological defects rather than inflation generally produce non-Gaussian features but are computationally challenging [Avelino et al. 1998]. A notable exception to this dearth of alternatives is the ingenious isocurvature model of Peebles [Peebles 1999a, Peebles 1999b].