BAYESIAN REASONING VERSUS CONVENTIONAL STATISTICS IN HIGH ENERGY PHYSICS
G. D'Agostini
Dipartimento di Fisica dell'Università ``La Sapienza''
Piazzale Aldo Moro 2, I-00185 Roma (Italy)
Email: dagostini@roma1.infn.it
URL: http://www-zeus.roma1.infn.it/~agostini/
Abstract.
The intuitive reasoning of physicists in conditions of uncertainty
is closer to the Bayesian approach than to the frequentist
ideas taught at University and which are considered the
reference framework for handling statistical problems. The combination
of intuition and conventional statistics allows practitioners
to get results which are very close, both in meaning and in numerical
value, to those obtainable by Bayesian methods, at least in simple
routine applications. There are, however, cases in which
``arbitrary'' probability inversions produce unacceptable or
misleading results and in these cases
the conscious application of Bayesian reasoning
becomes crucial. Starting from these considerations, I will finally
comment on the often debated question:
``is there any chance that all physicists will become Bayesian?''
Key words: Subjective Bayesian Theory, High Energy Physics, Measurement
Uncertainty
High Energy Physics
(HEP) is well known for using
very sophisticated detectors,
status of the art computers, ultra-fast data acquisition systems,
and very detailed (Monte Carlo) simulations. One might imagine
that a similar level of refinement
could be found in its analysis tools, on the trail of
the progress in probability theory and statistics of the
past half century. Quite the contrary! As pointed out by
the downhearted Zech
[1],
``some decades ago physicists were usually well educated
in basic statistics in contrast to their colleagues in social and
medical sciences. Today the situation is almost reversed.
Very sophisticated methods are used in these disciplines, whereas
in particle physics standard analysis tools available in many program
packages seem to make knowledge of statistics obsolete. This leads
to strange habits, like the determination of a r.m.s. of a sample
through a fit to a Gaussian. More severe are a widely spread
ignorance about the (lack of) significance of
I don't think that researchers in medical science or in biology
have a better statistics education than physicists. On the contrary,
their usually scant knowledge of the subject forces them to
collaborate with professional statisticians, and this is the reason
why statistics journals contain plenty of papers in which sophisticated
methods are developed to solve complicated problems in the
aforementioned fields. Physicists, especially in HEP, tend to be
more autonomous, because of their
skills in mathematics and computing, plus of a good dose of intuition.
But one has to admit that it is rather unlikely that a physicist, in a
constant hurry to publish results before anybody else,
can reinvent methods which have been reached by others after years of
work and discussion. Even those physicists who are considered experts in
statistics usually read books and papers written and refereed
by other physicists. The HEP community remains, therefore, isolated
with respect to the mainstream of research in probability and statistics.
In this paper I will not try to review all possible
methods used in HEP, nor to make a detailed comparison between
conventional and Bayesian solutions to solve the same problems.
Those interested in this kind of statistical and historical study
are recommended to look at the HEP databases and electronic archives
[5].
I think that the participants
in this workshop are more interested in learning about
the attitude of HEP physicists towards the fundamental aspects
of probability, in which framework they make uncertainty statements,
how subjective probability is perceived, and so on.
The intention here will be,
finally, to contribute to the debate around the
question ``Why isn't everybody a Bayesian''
[2],
recently turned into ``Why isn't every physicist a Bayesian''
[6].
The theses which I will try to defend are:
Some of the points sketched quickly in this paper are discussed
in detail in lecture notes
[7]
based on several seminars
and minicourses given over the past years. These notes also contain
plenty of general and HEP inspired applications.
1 I prefer to call the frequentist approach
``conventional'' rather than ``classical''.
Back.
2 Who can have failed to experience
endless discussions about trivial statistical problems, the solution
of which was finally accepted just because of the (scientific or, more
often, political) authority of somebody, rather than
because of the strength of the logical arguments?
Back.
3 I know a senior physicist
who used to teach students that
standard deviation is meaningful only for the Gaussian, and that
it is ``defined'' as half of
the interval around the average which contains 68% of the events!
More common is the evaluation of the standard deviation of a data sample
fitting a Gaussian to the data histogram
(see also the previous quotation of Zech
[1]), even
in those cases in which the histogram has nothing to do with
a Gaussian. The most absurd
case I have heard of is that of someone
fitting a Gaussian to a histogram exhibiting a flat shape
(and having good reasons for being considered to come from coming from
a uniform distribution)
to find the resolution of a silicon strip detector!.
Back.
4 For instance, the 1998 issue of the Review
of Particle Physics
[3]
includes an example based on this kind
of mistake with the intention to
show that ``the Bayesian methodology ...is not
appropriate for the objective presentation of experimental data''
(section 29.6.2, pag. 175).
Back.
5 Who has never come across somebody
calculating the ``error'' on the efficiency
6 In the past,
the correlation matrix was for many HEP physicists
``that mysterious list of numbers
printed out by MINUIT'' (MINUIT
[4]
is the minimization/fitting package mostly
used in HEP), but at least some cared
about understanding what those numbers meant and how to use them
in further analysis. Currently - I agree with Zech
[1]
- the situation has worsened:
although many people do take into account correlations,
especially in combined analysis of crucial Standard Model parameters,
the interactive packages, which display only
standard deviations of fitted parameters, tend to ``hide'' the
existence of correlations
to average users.
Back.
An idea well rooted among physicists, especially nuclear and particle
physicists, is that the result of a measurement must be reported
with a corresponding uncertainty. What makes the
measured values subject to a degree of uncertainty
is, it is commonly said,
the effect of unavoidable measurement errors,
usually classified as random (or statistical) and
systematic
(7) .
Uncertainties due to statistical errors are commonly treated using the
frequentist concept of confidence intervals, although the procedure
is so unnatural that the interpretation of the result is unconsciously
subjective (as will be shown in a while),
and there are known cases (of great relevance in frontier
research) in which this approach is not applicable.
As far as uncertainties due to systematics errors are concerned,
there is no conventional consistent theory to handle them,
as is also indirectly recognized by the ISO Guide
[10].
The ``fashion'' at the moment is to add them quadratically if they are
considered to be independent, or to build a covariance matrix if not.
This procedure is not justified theoretically (in the frequentist approach)
and I think that it is used essentially because of the reluctance of
experimentalists to add linearly the dozens
of contributions of a complicated HEP measurement, as the old fashioned
``theory'' of maximum errors
suggests doing (8) .
The pragmatic justification for the
quadratic combination of ``systematic errors'' is that one is using
a rule (the famous ``error propagation''
formula (9) )
which is considered to be valid at least for ``statistical
errors''. But, in reality, this too is not correct.
The use of this formula is again arbitrary in the case
of ``statistical errors'', if these have been
evaluated from confidence intervals
(10) .
In fact, there is no logical reason
why a probabilistic procedure proved for standard deviations of
random variables (the observables) should also be valid
for 68% confidence intervals, which is considered, somehow,
an uncertainty attributed to the true value.
These examples show quite well the
contradiction between
the cultural background on probability and the practical good sense
of physicists. Thanks to this good sense, frequentist ideas are
constantly violated, with the positive effect that at least
some results are obtained
(11) .
It is interesting to notice that in simple routine applications
these results are very close, both in value and in meaning, to those
achievable starting from what I consider to be the
correct point of view for handling
uncertainty (subjective probability). There are, on the other hand,
critical cases in which scientific conclusions may be seriously
mistaken. Before discussing these cases, let us look more closely
at the terms of the claimed contradiction.
7 This last statement may
sound like a tautology, since ``error'' and
``uncertainty'' are often used as synonyms. This
hints to the fact that in this subject there is
neither uniformity of language, nor of methods, as is recognized
by the metrological organizations, which have made
great efforts to bring some order into the
field [8,
9,
10,
11,
12].
In particular, the International Organization for Standardization
(ISO) has published ``Guide to the expression of uncertainty
in measurement''
[10],
containing definitions, recommendations
and practical examples. For example, error is defined
as ``the result of a measurement minus a true value of the measurand''
uncertainty ``a parameter, associated with the result of a measurement,
that characterize the dispersion of the values that could reasonably be
attributed to measurand'', and, finally, true value ``a value
compatible with the definition of the given particular quantity''.
One can easily see that it is not just a question of practical
definitions. It seems to me that
there is a well-thought-out philosophical
choice behind these definitions,
although it is not discussed extensively in the Guide.
Two issues
in the Guide that I find of particular importance are the
discussion on the sources of uncertainty and the admission
that all contributions to the
uncertainty are of a probabilistic nature.
The latter is strictly related to the
subjective interpretation of probability, as
admitted by the Guide and discussed in depth
in [7].
(The reason why these comments on the ISO Guide have been
placed in this long footnote is that, unfortunately,
the Guide is not yet
known in the HEP community and, therefore, has no influence
on the behaviour of HEP physicists about which I am going
to comment here.
This is also the reason why I will often use in this paper
typical expressions currently used in HEP and
which are in disagreement with the ISO recommendations.
But I will use these expressions preferably within quote marks,
like ``systematic error'' instead of ``uncertainty due to
a recognized systematic error of unknown size''.)
Back.
8 In fact, one can see that when there
are only 2 or 3
contributions to the ``systematic error'', there are still people who
prefer to add them linearly.
Back.
9 The most well-known version is that in
which correlations are neglected:
Y stands for the quantity of interest, the value
of which depends
on directly measured quantities,
calibration constants and other
systematic effects (all terms generically indicated by Xi).
This formula
comes from probability theory,
but it is valid if Xi and Y are
random variables,
10 As
far as ``systematic errors'' are concerned the situation
is much more problematic because the ``errors'' are not even
operationally well defined: they may correspond to
subjectivist standard deviations (what I consider to be correct,
and what corresponds to the ISO type B standard uncertainty
[10]),
but they can more easily be maximum deviations, ±50% variation
on a selection cut, or the absolute difference obtained using two
assumptions for the systematic effect.
Back.
11 I am strongly convinced
that a rigorous application of frequentist ideas leads nowhere.
Back.
If one asks HEP physicists ``what is probability?'', one will
realize immediately that they ``think they are'' frequentist.
The same impression is got looking at the books and
lecture notes they use
[13].
Particularly significant, to get an overview of ideas and methods
commonly used, are the PDG
[3]
and other booklets
[14,
15]
which have a kind of explicit (e.g.
[3,
14])
or implicit (e.g.
[15])
imprimatur of HEP organizations.
If, instead, one asks physicists what they think about probability
as ``degree of belief'' the reaction is negative and
can even be violent: ``science must be objective: there is no room
for belief'', or ``I don't believe something. I assess it. This is
no a matter for religion!''.
3.2. HEP physicists ``are Bayesian''
On the other hand,
if one requires physicists to express their opinion about
practical situations in condition of uncertainty,
instead of just standard examination questions,
one gets a completely different impression. One realize vividly
that Science is indeed based on beliefs,
very solid and well grounded beliefs, but they remain beliefs
``...in instrument types, in programs of experiment enquiry,
in the trained, individual judgements about every local behavior
of pieces of apparatus''
[16].
Physicists find it absolutely natural to talk
about the probability of hypotheses, a concept for which there is no
room in the frequentist approach. Also the intuitive
way with which they figure out the result is, in fact, a
probabilistic assessment on the true value.
Try to ask what is the probability that the top quark mass is
between 170 and 180 GeV. No one
(12)
will reply that the question has no sense, since ``the top quark
mass is a constant of unknown value'' (as an orthodox frequentist
should complain).
They will simply answer that the probability is such and such percent,
using the published value and ``error''.
They are usually surprised if somebody tries to explain to
them that they ``are not allowed'' to speak of probability of a true value.
Another word which physicists find scandalous is ``prior''
(``I don't want to be influenced by prejudices'' is the usual reply).
But in reality priors play a very important role in laboratory
routines, as well as at the moment of deciding that a paper is ready for
publication. They allow experienced physicists to realize that
something is going wrong, that a student has most probably made a serious
mistake, that the result has not yet been corrected by all systematic
effects, and so on. Unavoidably, priors generate
some subtle cross correlations among results, and there are well known cases
of the values of physics quantities slowly drifting from an initial
point, with all subsequent results being included in the ``error bar''
of the previous experiment. But I think that
there no one and nothing is to blame for the fact
that these things happen (unless made on purpose): a strong evidence is needed
before the scientific community radically changes its mind,
and such evidence is often achieved after a long series of
experiments. Moreover, very subtle systematic effects
may affect the data, and it is not a simple task for an experimentalist
to decide when all corrections have been applied, if he has no idea
what the result should be.
3.3. Intuitive application of Bayes' theorem
There is an example which I like to give, in order to
demonstrate that the intuitive reasoning
which unconsciously transforms confidence intervals into
probability intervals for the true value is, in fact, very close
to the Bayes' theorem. Let us imagine we see a hunting dog in a forest
and have to guess where the hunter is, knowing that there is a
50% probability that the dog is within 100 m around him.
The terms of the analogy
with respect to observable and true value are obvious.
Everybody will answer immediately that, with 50% probability,
the hunter is within 100 m from the dog. But everybody will also agree
that the solution relies on some implicit assumptions:
uniform prior
distribution (of the hunter in the forest) and
symmetric likelihood (the dog has no preferred direction,
as far as we know, when he runs away from the hunter).
Any variation in the assumptions leads to a different
solution. And this is also easily recognized by physicists,
expecially HEP physicists, who are aware of situations in which
the prior is not flat (like the cases
of a bremsstrahlung photon or of a cosmic ray spectrum)
or the likelihood is not symmetric (not all detectors have a nice
Gaussian response). In these situations intuition may still help a
qualitatively guess to be made about
the direction of the effect on the value of the measurand,
but a formal application of the Bayesian ideas
becomes crucial in order to state a result which is consistent with what
can be honestly learned from data.
The fact that Bayesian inference is not currently used in HEP
does not imply
that non-trivial inverse problems remain unsolved, or that
results are usually wrong. The solution often relies on extensive
use of Monte Carlo (MC)
simulation (13)
and on intuition. The inverse problem is then
treated as a direct one. The quantities of interest are
considered as MC parameters, and
are varied until the best statistical agreement between simulation
output and experimental data is achieved. In principle, this is
a simple numerical implementation of Maximum Likelihood, but in reality
the prior distribution is also taken into account in the simulation
when it is known to be non uniform (like in the aforementioned
example of a cosmic ray experiment). So, in reality what it is often
maximized is not the likelihood, but the Bayesian posterior
(likelihood × prior), and, as said before, the result is intuitively
considered to be a probabilistic statement for the true value.
So, also in this case, the results are close to those obtainable
by Bayesian inference, especially if the
posterior is almost Gaussian (parabolic negative log-likelihood).
Problems may occur, instead, when the ``not used'' prior
is most likely not uniform, or when the posterior is
very non-Gaussian. In the latter case the difference between
mode and average of the distribution, and the evaluation of the uncertainty
from the ``
12 Certainly one may find people
aware of the ``sophistication'' of the frequentist approach,
but these kinds of probabilistic statements are
currently heard in conferences and no
frequentist guru stands up to complain that the speaker is talking
nonsense.
Back.
13 If there is something in which HEP
physicists really believe, it is
Monte Carlo simulation! It plays a crucial role in all analyses,
but sometimes its use as a multipurpose brute force problem solver
is really unjustified and it can, from a cultural point of view,
be counterproductive. For example,
I have seen it applied to solve elementary
problems which could be solved analytically, like ``proving'' that
the variance of the sum of two random numbers is the sum of the variances.
I once found a sentence at the end of the solution
of a standard probability problem which I consider to
be symptomatic of this brute force behaviour:
``if you don't trust logic, then you can make a little Monte Carlo...''.
Back.
Besides the intuitive use of Bayesian reasoning, there
are, in fact, some applications in which the Bayes' theorem
is explicitly applied. This happens when frequentist methods
``do not work'', i.e. they give
manifestly absurd results,
or in solving more complicated problems than just
inferring the value of a quantity, like, for example, the deconvolution
of a spectrum (``unfolding''). Nevertheless, these methods are
mostly used with a utilitarian spirit, without
having really understood the meaning of subjective probability, or even
remaining skeptical about it. They are used as one uses one of
the many frequentist ``ad hoc-eries''
(14) ,
after it has been ``proved''
that they work by MC
simulation (15) .
Some of the cases in which the conventional methods do not work
have even induced the PDG
[3]
to present Bayesian methods. But, according to the PDG, a paper
published this year
[18]
finally gives a frequentist solution to the problems, and this
solution is recommended for publishing the results. Let us review
the situation citing directly
[18]:
``Classical confidence intervals
are the traditional way in which high energy physicists report errors
on results of experiments. ... In recent years, there has been
considerable dissatisfaction ...for upper confidence limits...
This dissatisfaction led the PDG to describe procedures for Bayesian
interval construction in the troublesome cases: Poisson processes
with background and Gaussian errors with a bounded physical region.
... In this paper, we...use (...) to
obtain a unified set of classical confidence
intervals for setting upper limits and quoting two-sided confidence
intervals. ...We then obtain confidence intervals which are
never unphysical or empty. Thus they remove an original motivation
for the description of Bayesian intervals by the PDG.''
In fact, the 1998 issue of the Review
of Particle Physics still exhibits
the Bayesian approach (with the typical misconceptions
that frequentists have about it), but then it suggests two papers by
frequentists
[6,
2]
(``a balanced discussion''
[3])
to help practitioners to form their own idea on the subject, and, finally,
it warmly recommends the new frequentist approach.
It is easy to imagine what the reaction
of the average HEP physicist will be when confronted by
the authority of the PDG, unaware
that ``the PDG'' which rules analysis methods is in reality constituted of
no more than one or two persons who recommend a paper written by
their friends (as is clear from the references and the cross
acknowledgements). One should also notice
that this paper claims important progress in statistics,
but was in fact published in a physics journal (I wonder what
the reaction of a referee of a
statistics journal would have been...).
In conclusion, there is still a large gap between good sense
and the dominating statistical culture. For this reason we must still be
very careful in interpreting published results and in
evaluating whether or not the conventional methods used lead to
correct scientific conclusions ``by chance''.
Some cases of misleading results will be described
in the next section.
14 For example,
this was exactly the attitude which I had some years ago, when I wrote a
Bayesian unfolding program
[17],
and that of the large majority my
colleagues who still use the program. Now, after having attended
the 1998 Valencia Meeting on Bayesian Statistics, I have realized
that this pragmatic frequentist-like use of Bayesian methods
is rather common.
Back.
15 I would like to point out that
sometimes the conclusions derived from
MC checks of Bayesian procedures may be
misleading, as discussed in detail in
[7].
Back.
As already discussed, confidence levels are intuitively thought
(and usually taught) as probabilities for the true values.
I must recognize that many frequentist books do insist
on the fact that the probability statement is not referred
to the true value. But then, when these books have to explain the
``real meaning'' of the result, they are forced to use ambiguous
sentences which remain stamped in the memory of the reader much more than the
frequentistically-correct twisted reasoning that they
try to explain. For example Frodesen et al.
[13]
speak about ``the faith we attach to this statement'', as if
``faith'' was not the same as degree of belief...);
Eadie et al.
[13]
introduce the argument saying that
``we want to find the range ...which contains the true value
Similarly, significance levels are usually taken
as probability of the tested hypothesis. Also this
non-orthodox interpretation is stimulated by sentences like
``in statistical context, the words highly significant
mean proved beyond a reasonable doubt''.
It is also well known that the arbitrary translation of
p-values into probability of the null hypothesis
produces more severe mistakes than those concerning
the use of confidence interval for uncertainty statements on true values.
Let us consider some real life examples
of the misinterpretation of the two kinds just described.
5.1. Claims of new physics based on p-values
You may have heard in past years some rumors, or even
official claims, of discoveries of ``New Physics'', i.e. of
phenomenology which goes behind the so called Standard Model
of elementary particles. Then, after some time, these announcements
were systematically recognized as having been false alarms,
with a consequent reduction in the credibility of the HEP
community in the eyes of public opinion and tax payers (with easily imaginable
long term aftermath for government support of this research).
All these fake discoveries were based on considering low p-values
as probability of the null hypothesis ``no new effect''.
The most recent example of this kind
is the so called 1997 ``HERA high Q2 events excess''.
The H1 and ZEUS collaborations, analyzing data collected at the HERA
very high energy electron-proton collider in Hamburg (Germany), found
an excess of events (with respect to expectations) in the kinematical
region corresponding to very hard interactions
[19].
The ``combined significance''
(17)
of the excess was of the order of 1%.
Its interpretation as a hint of new physics was even suggested
by official statement by the laboratory and by other agencies.
For example the DESY official statement was ``...the joint
distribution has a probability of less than one percent to come
from Standard Model NC DIS processes''
[22]
(then it implies ``it has a > 99%
probability of not coming from the standard
model!'' (18) ).
Similarly, the Italian INFN reported that ``la
probabilità che gli eventi osservati siano una fluttazione
statistica è inferiore all'1%'' (then,
it implies that ``with 99% probability,
the events are not a statistical fluctuation, i.e. new physics''!).
This is the reason why the press reported the news as
``scientists are practically sure they have found new physics''.
What I found astonishing is that most of the people I talked to
had real difficulty in understanding that this probability inversion
is not legitimate. Only when I forced them to state
their degree of belief using the logic of the coherent bet
did it emerge that most of my colleagues would not even place a
1:1 bet in favour of the new discovery. Nevertheless,
they were in favour of publishing the result because the loss
function was absolutely unbalanced
(an indirect Nobel prize against essentially nothing).
5.2. What does a lower mass bound mean?
The second example concerns
confidence intervals, and it comes from new particle search. This has
always been one of the main activities of HEP.
New particles are postulated by theories and experimentalists
look for evidence for them in experimental data. Usually,
if the particle is not ``observed''
(19)
one says that, although
the observation does not disprove the existence of the particle,
this is an indication of the fact that the particle is ``too heavy''.
The result is then quantified by a ``lower bound'' at a
``95% confidence level''. Without entering into detail
of how the limit is operationally defined (see, e.g.,
[24] and
references therein, in particular
[25],
to have an idea of the level of complication
reachable to solve a simple problem),
I want to point out that also in this case the
result can be misleading. Again I will give a real life
example. A combined analysis of all the
LEP experiments on the Higgs mass concluded recently that
``A 95% confidence level lower bound of 77.5 GeV/c2 is
obtained for the mass of the Standard Model Higgs
boson'' (20) .
This sounds as if one were sure at 95% that the mass is above
the quoted bound. In fact, most of the people I
interviewed about the meaning of the statement, even those belonging to
the LEP experimental teams, answered ``if the Higgs boson
exists at all, then there is 95% probability
that its mass is above the limit''. There were also a few people
who answered ``if I do a MC simulation of the decay of a 77.5 GeV Higgs
boson, I get in only 5% of the cases the simulation describing the data'',
or ``if there is an Higgs boson and its mass is less than 77.5 GeV,
then the observations of the search experiments have a probability of
at most 5% of being correct'', or something similar.
From all of which it is
very difficult to understand, from a logical point of view, why
one should be 95% confident that the mass is higher than the
bound (21) .
The problem can be solved easily with Bayesian methods (see
[7]
for details). Assuming a flat prior for the mass, one
finds that the value of the lower bound is more or less
the published one, but only under the condition that
the mass does not exceed the kinematical limit of the studied reaction.
But this limit is just a few GeV above the stated lower bound.
Thus in order to obtain the correct result one needs to renormalize
the probability taking account of the possible range of masses above the
kinematical limit and for which the
experiment has no sensitivity. For this reason, in the case of
[24]
the probability that
the mass value is above 77.5 GeV/c2 may easily become 99.9%,
or more, depending on the order of magnitude of a possible upper
bound for the mass.
Then, in practice these lower bounds can be taken as
certainties (22) .
16 I think that Aristoteles would have
gotten mad if
somebody had tried to convince him that the proposition
``the range contains
17 Physicists are not familiar
with the term p-value (readers not familiar with this
term may find a concise review in
[20]).
Moreover, they are usually not aware of the implications
of the fact that the statistical significance takes into account
also the probability of unobserved data (see, e.g.,
[21]).
Back.
18 One might think that
the misleading meaning of that sentence
was due to unfortunate wording, but this
possibility is ruled out by other statements which show
clearly a quite odd point of view of probabilistic matter.
In fact the DESY 1998 activity report
[23]
insists in saying that ``the likelihood that the data produced is the result
of a statistical fluctuation, ..., is equivalent to that
of tossing a coin and throwing seven 'heads' or 'tails'
in a row'' (replacing 'probability' by 'likelihood' does
not change the sense of the message).
Then, trying to explain the meaning of a
statistical fluctuation, the following example is given:
``This process can be simulated with a die.
If the number of times a die is
thrown is sufficiently large, the die falls equally often on all faces,
i.e. all six numbers occur equally often. The probability for
each face is exactly a sixth or 16.66% - assuming the die
is not loaded. If the die is thrown less often, then the probability
curve for the distribution of the six die values is no longer a straight
line but has peaks and troughs. The probability distribution
obtained by throwing the die varies about the theoretical value
of 16.66% depending on how many times it is thrown''.
Back.
19 This concept of ``observation''
is not like that of seeing a black swan,
to mention a famous classical example. New particles leave
signatures in the detector that on an event by event basis
cannot be distinguished by other processes (background).
A statistical (inferential) analysis is therefore needed.
Back.
20 In the meanwhile new data have
increased this limit, but the actual number is irrelevant for this discussion.
Back.
21 There was also somebody who refused
to answer because ``your question is going to be difficult to answer'', or
without any justification (perhaps they
realized that it was impossible to explain the statement
to a scientific journalist, or to a government authority - these were
the terms of my question - without using probabilistic statements
which were incompatible with what they thought about probability).
Back.
22 There are in fact theorists who ``assume''
the lower bounds as certain bounds in their considerations.
Perhaps they do it intuitively, or because they have
heard in the last decades of thousands of these 95% lower bounds,
and never a particle has then shown up in the 5% side...
Back.
Finally, I would like to give a last recommendation. Don't try
to convince a physicist that he already is Bayesian, or that
you want to convert him to become Bayesian.
A physicist feels offended if you call
him ``X-ian'', be it Newtonian, Fermian, or Einsteinian.
But, being human, he has a natural feel for
probability, just like everybody else.
I would like to generalize this idea and propose
reducing the use of the adjective
``Bayesian''. I think that the important thing is to have
a theory of uncertainty in which ``probability'' has the same meaning
for everybody, precisely that meaning which the human mind has
naturally developed and that frequentists have tried to kill.
Therefore I would rather call these methods probabilistic
methods. And I conclude saying that, obviously,
``I am not a Bayesian''.
It is a pleasure to thank the organizers of Maxent98
for the warm hospitality in Garching, which favoured
friendly and fruitful discussions among the participants.
23 For example
frequentists completely
misunderstand this points, when they state, e.g.,
that ``Bayesian methods proceed by invoking an interpretation of
Bayes' theorem, in which one deems it sensible to consider a p.d.f.
for the unknown true value mt'', or
that ``a pragmatist can consider the utility of equations
generated by the two approaches while skirting the issue of
buying a whole philosophy of science'
[6].
I find that also the Zellner's paper
[26]
demonstrating that Bayes' theorem makes the best use of the
available information can
help a lot to convince people.
Back.
24 Although it may seem absurd,
the Bayesian approach is recognized by ``frequentists''
to be ``well adapted to decision-making situations''
[3]
(see also
[6,
18]).
I wonder what then probability is for these authors.
Back.
25 Dogmatism is never desirable. It can
be easily turned against the theory. For example, one criticism of
[18]
says, more or less, that
Bayesian theory supports Jeffreys' priors, and not uniform priors,
but, since Jeffreys' priors give unreasonable results in their
application, then one should mistrust Bayesian methods! (see also
[28].)
One may object that the
meaning and the role of Jeffreys' priors was misunderstood,
but it seems to me difficult to control the use of objective priors
or of reference analysis once they have left the community
of experts aware of the ``rather special nature and role
of the concept of a `minimally informative' prior specification
- appropriately defined!''
[29].
Back.
 INTRODUCTION
INTRODUCTION
 MEASUREMENT UNCERTAINTY
MEASUREMENT UNCERTAINTY
 PROFESSED FREQUENTISM VERSUS PRACTICED SUBJECTIVISM
PROFESSED FREQUENTISM VERSUS PRACTICED SUBJECTIVISM
 HEP physicists ``are frequentist''
HEP physicists ``are frequentist''
 HEP physicists ``are Bayesian''
HEP physicists ``are Bayesian''
 Intuitive application of Bayes' theorem
Intuitive application of Bayes' theorem
 Bayes versus Monte Carlo
Bayes versus Monte Carlo
 EXPLICIT USE OF BAYESIAN METHODS IN HEP
EXPLICIT USE OF BAYESIAN METHODS IN HEP
 EXAMPLES OF MISLEADING RESULTS INDUCED BY
CONVENTIONAL STATISTICS
EXAMPLES OF MISLEADING RESULTS INDUCED BY
CONVENTIONAL STATISTICS
 CONCLUSIONS
CONCLUSIONS
 REFERENCES
REFERENCES
1. INTRODUCTION
 2
tests with a large number of bins and missing experience
with unfolding methods''. In my opinion, the main reason
for this cultural gap is that statistics and probability are not given
sufficient importance in the student curricula: ad hoc formulae
are provided in laboratory courses to report the ``errors'' of measurements;
the few regular lectures on ``statistics'' usually mix up
descriptive statistics, probability theory and
inferential statistics.
This leaves a lot of freedom for personal interpretations of the
subject (nothing to do with subjective probability!).
Of equal significance is the fact that
the disturbing catalog of inconsistencies
[2]
of ``conventional'' (1)
statistics helps to give the impression that this subject is matter of
initiates and local gurus, rather than a scientific
discipline (2) .
The result is that standard knowledge of statistics at
the end of the University curriculum is insufficient and confused,
as widely recognized. Typical effects of this (dis-)education are the
``Gaussian syndrome''
(3)
(from which follows the uncritical use of the rule of combining results,
weighing them with inverse of the ``error'' squared
(4) ,
or the habit of calling
2
tests with a large number of bins and missing experience
with unfolding methods''. In my opinion, the main reason
for this cultural gap is that statistics and probability are not given
sufficient importance in the student curricula: ad hoc formulae
are provided in laboratory courses to report the ``errors'' of measurements;
the few regular lectures on ``statistics'' usually mix up
descriptive statistics, probability theory and
inferential statistics.
This leaves a lot of freedom for personal interpretations of the
subject (nothing to do with subjective probability!).
Of equal significance is the fact that
the disturbing catalog of inconsistencies
[2]
of ``conventional'' (1)
statistics helps to give the impression that this subject is matter of
initiates and local gurus, rather than a scientific
discipline (2) .
The result is that standard knowledge of statistics at
the end of the University curriculum is insufficient and confused,
as widely recognized. Typical effects of this (dis-)education are the
``Gaussian syndrome''
(3)
(from which follows the uncritical use of the rule of combining results,
weighing them with inverse of the ``error'' squared
(4) ,
or the habit of calling  2
any sum of squared differences between fitted curves and data points,
and to use it as if it were a
2
any sum of squared differences between fitted curves and data points,
and to use it as if it were a
 2),
the abused ``
2),
the abused ``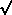 n rule''
to evaluate ``errors'' of counting experiments
(5)
and the reluctance to take into account correlations
(6) ,
just to remain at a very basic level.
n rule''
to evaluate ``errors'' of counting experiments
(5)
and the reluctance to take into account correlations
(6) ,
just to remain at a very basic level.
 = n / N, using
the standard ``error propagation'' starting from
= n / N, using
the standard ``error propagation'' starting from
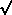 n
and
n
and 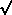 N ?
Back.
N ?
Back.
2. MEASUREMENT UNCERTAINTY

 (Xi) are
standard deviation and the linearization is reasonable.
It is very interesting to look
at text books to see how this formula is derived.
The formula is usually initially proofed referring to random variables
associated to observables and then, suddenly, it is referred
to physics quantities, without any justification.
Back.
(Xi) are
standard deviation and the linearization is reasonable.
It is very interesting to look
at text books to see how this formula is derived.
The formula is usually initially proofed referring to random variables
associated to observables and then, suddenly, it is referred
to physics quantities, without any justification.
Back.
3. PROFESSED FREQUENTISM VERSUS PRACTICED SUBJECTIVISM
3.1. HEP physicists ``are frequentist''
 (log-likelihood)
= 1/2 rule'' can make quite a difference to the result.
(log-likelihood)
= 1/2 rule'' can make quite a difference to the result.
4. EXPLICIT USE OF BAYESIAN METHODS IN HEP
5. EXAMPLES OF MISLEADING RESULTS INDUCED BY CONVENTIONAL
STATISTICS
It is well known that the frequentist denial of the
concept of probability of hypotheses leads to misleading results in all
cases in which the simple ``dog-hunter inversion paradigm''
is violated. This also happens in HEP.
 ° with probability
° with probability
 ''
(16) ; and so on.
''
(16) ; and so on.
 ° with
probability
° with
probability  ''
does not imply
``
''
does not imply
`` ° is in
that range with probability
° is in
that range with probability
 ''.
Back.
''.
Back.
6. CONCLUSIONS
Although it is clear that the dominant statistical culture is still
frequentism in HEP (and everywhere else), I am myself rather
optimist on the possibility that
the situation will change, at least in HEP, and that Bayesian
reasoning will emerge from an intuitive to a
conscious level. This is not a dream (although clearly several academic
generations are still needed) if the theory is
presented in a way that it is acceptable to an ``experienced physicist''.
 2 fit
I consider myself to be using a Bayesian method,
although in a simplified form. This attitude contrasts
to that of practitioners who use methods in which the Bayes' theorem
is explicitly applied, but as if it were one of the many
frequentist cooking recipes.
2 fit
I consider myself to be using a Bayesian method,
although in a simplified form. This attitude contrasts
to that of practitioners who use methods in which the Bayes' theorem
is explicitly applied, but as if it were one of the many
frequentist cooking recipes.
Acknowledgements
REFERENCES
G. Zech, ``Comparing statistical data to Monte Carlo simulation -
parameter fitting and unfolding'', DESY 95-113, June 1995.
B. Efron, ``Why isn't everyone a Bayesian?'',
Am. Stat. 40 (1986) 1.
PDG stands for Data Particle Group, which edits the
``Review of particle physics'',
a very influential collection of data, formulae and methods,
including sections on Probability and Statistics.
The latest issues are:
R.M. Barnet et al. Phys. Rev. D 54 (1996) 1;
C. Caso et al. Eur. Phys. J. C3 (1998) 1
(http://pdg.lbl.gov/).
F. James and M. Roos, ``MINUIT - system for function minimization
and analysis of the parameter errors and correlations'',
Comp. Phys. Comm. 10 (1975) 343.
http://www.slac.stanford.edu/spires/hep,
http://xxx.lanl.gov/,
http://alice.cern.ch/Preprints,
http://wwwas.cern.ch/library/hepdoc/hepdoc.html,
http://www-lib.kek.jp/publib.html.
R.D. Cousins, ``Why isn't every physicist a Bayesian?'',
Am. J. Phys. 63 (1995) 398.
G. D'Agostini, ``Bayesian reasoning in High Energy Physics - principles
and applications'', lecture notes of the Academic Training given at
CERN (Geneva), May 25-29 1998. A draft is available on the web at
http://www.cern.ch/Training/ACAD/reglec_E.html.
DIN Deutsches Institut für Normung,
``Grunbegriffe der Messtechnick - Behandlung
von Unsicherheiten bei der Auswertung von Messungen''
(DIN 1319 Teile 1-4), Beuth Verlag GmbH, Berlin, Germany, 1985.
R. Kaarls, BIPM proc.-Verb. Com. Int.
Poids et Mesures 49 (1981), A1-A2 (in french);
P. Giacomo, Metrologia 17 (1981) 73 (draft of
english version; for the official BIPM translation see
[10] or [12]).
International Organization for Standardization (ISO),
``Guide to the expression of uncertainty in measurement'',
Geneva, Switzerland, 1993.
International Organization for Standardization (ISO),
``International vocabulary of basic and general terms in metrology'',
Geneva, Switzerland, 1993.
B.N. Taylor and C.E. Kuyatt,
``Guidelines for evaluating and expressing
uncertainty of NIST measurement results'', NIST Technical Note 1297,
September 1994;
(www:
http://physics.nist.gov/Pubs/guidelines/outline.html).
Without any attempt to be complete, I would like
to cite those which are more familiar to HEP physicists
(I have including also the Bayesian book by Sivia that has attracted
recently the attention of my colleagues):
M.C. Barford, ``Experimental measurements: precision, error and truth'',
John Wiley & Sons, 1985;
R.J. Barlow,
``Statistics'', John Wiley & Sons Ltd, Chichester, 1989;
P.R. Bevington and D.K. Robinson,
``Data Reduction
and Error analysis for the Physical Sciences'', McGraw-Hill, 1992;
S. Brandt, Statistics and computational methods in data analysis,
North-Holland, 1976;
G. Cowan, ``Statistical data analysis'', Clarendon Press, Oxford, 1998;
W. T. Eadie, D. Drijard, F. E. James, M. Roos, B. Sadoulet,
``Statistical Methods in Experimental Physics'',
North Holland, Amsterdam, 1971;
A. G. Frodeson, O. Skjeggestad, H. Tofte,
``Probability and Statistics in Particle Physics'',
Columbia University, New York, 1979;
L. Lyons, ``Statistics for nuclear and particle physicists'',
Cambridge University Press, 1986, reprinted 1992;
L. Lyons, ``A practical guide to data analysis for
physical science students'', Cambridge University Press, 1991;
A.M. Mood, F.A. Graybill and D.C. Boes, ``Introduction to the
theory of statistics'', McGraw-Hill, 1984.
L. G. Parrat,
``Probability and Experimental Errors in Science'',
John Wiley & Sons Ltd, 1994;
S. Rabinovich,
``Measurement Errors: Theory and Practice'',
American Institute of Physics, New York, 1993.
B. P. Roe,
``Probability and Statistics in Experimental Physics'',
Springer-Verlag New York Inc, 1992;
D.S. Sivia, ``Data analysis - a Bayesian tutorial'', Clarendon Press,
Oxford, 1996.
D.L. Smith, "Probability, Statistics and Data Uncertainties in
Nuclear Science and Technology", American Nuclear Society, 1991;
G. L. Squires, ``Practical physics'',
Cambridge University Press, third edition, 1985;
J.R. Taylor, ``An introduction for error analysis'', University
Science Books, 1982;
H.D. Young, ``Statistical analysis of experimental data'',
McGraw-Hill, 1962.
V. Blobel et al., ``Formulae and Methods in Experimental Data Evaluation'',
European Physical Society, 1984.
R.K. Bock and W. Krischer, ``The data analysis Briefbook'',
Springer, 1998
(http://www.cern.ch/Physics/DataAnalysis/BriefBook/)
P.L. Galison, ``How experiments end'',
The University of Chicago Press, 1987.
G. D'Agostini, ``A multidimensional unfolding method based
on Bayes' theorem'',
Nucl. Instr. Meth. A362 (1995) 487.
G.J. Feldman and R.D. Cousins, ``Unified approach to the classical
statistical analysis of small signal'',
Phys. Rev. D57 (1998) 3873,
April 1, 1998.
H1 Collaboration, C. Adloff et al.,
``Observation of events at very high Q2 in ep
collisions at HERA'', Z. Phys., C74 (1997) 191;
ZEUS Collaboration, J. Breitweg et al., ``Comparison of
ZEUS data with Standard Model predictions for
e+p -> e + X'',
Z. Phys., C74 (1997) 207.
M.J. Schervish, ``P values: what they are and what they
are not'', Am. Stat. 50 (1996) 203.
J.O. Berger and D.A. Berry, ``Statistical analysis and the illusion
of objectivity'', American Scientist 76 (1988) 159.
``DESY Science Information on Recent HERA Results'',
Feb. 19, 1997,
http://www.desy.de/pr-info/desy-recent-hera-results-feb97_e.html.
DESY'98 - Highlights from the DESY Research Center,
``Throwing 'heads' seven times in a row - what if it was just a statistical
fluctuation?'' (report obtainable free of charge by DESY:
http://www.desy.de).
P. Bock et al. (ALEPH, DELPHI, L3 and OPAL Collaborations),
``Lower bound for the standard model Higgs boson mass from combining
the results of the four LEP experiments'', CERN-EP/98-046,
April 1, 1998.
P. Janot and F. Le Diberder, ``Combining 'limits' '',
CERN-PPE-97-053, May 1997.
A. Zellner, ``Optimal information processing and Bayes's theorem'',
Am. Stat. 42 (1988) 278 (with discussion by E.T. Jaynes, B.M. Hill,
J.M. Bernardo and S. Kullback).
B. de Finetti, ``Theory of probability'',
J. Wiley & Sons, 1974.
G. D'Agostini, ``Jeffreys priors versus experienced
physicist priors'', contributed paper to the 6th Valencia
International Meeting on Bayesian Statistics, May 30th - June 4th, 1998,
Alcossebre (Spain),
physics/9811045.
J.M. Bernardo, A.F.M. Smith,
``Bayesian theory'', John Wiley & Sons Ltd, 1994.