Annu. Rev. Astron. Astrophys. 1998. 36: 435-506 Copyright © 1998 by Annual Reviews. All rights reserved

7. INTERNAL KINEMATICS OF LOCAL GROUP DWARFS

For a given mass-to-light ratio, the central velocity dispersion of a self-gravitating system in equilibrium scales as (R_cS₀)^1/2, where r_c is the characteristic radial scale length of the system and S₀ is the central surface brightness in intensity units (Richstone & Tremaine 1986). Globular clusters have central velocity dispersions of 2-15 km s^-1. Pressure-supported dwarf galaxies that have central scale lengths about 10 times larger and surface brightnesses 10³ times smaller should therefore have central velocity dispersions of 2 km s^-1. They don't. All low-luminosity dwarfs have central velocity dispersions of 7 km s^-1, independent of galaxy type and regardless of whether the dispersion is measured from the stars or gas. In this section, I review the observational basis for DM in the dwarf galaxies of the Local Group, and discuss some possible alternatives to DM in these systems. The seminal paper of this field was written by Aaronson (1983). Recent reviews include those by Gallagher & Wyse (1994), Mateo (1994), Pryor (1994, 1996), Gerhard (1994), Olszewski (1998).

7.1. The Observational Basis for Dark Matter

To estimate kinematic masses for galaxies, we require a measure of the velocity dispersion for pressure-supported systems, or the rotation velocity for rotationally supported galaxies, and an estimate of the relevant scale length. To determine mass-to-light ratios, we further need the luminosity density or total luminosity. The scale length required depends on the details of the dynamical model used to interpret the kinematics; for nonrotating dwarfs, the King core radius or exponential scale length is commonly used (Table 3), whereas for rotating systems, the relevant length scale is taken from the rotation curve (Table 7).

DSPH GALAXIES     Because they generally lack an ISM component (or when they do, it is not in dynamical equilibrium; see Section 4) and because they have such low surface brightnesses, the internal kinematics of most Local Group dSph galaxies are based on high-precision spectroscopic radial velocities of individual stars (Mateo 1994, Olszewski 1998). There have been at least four persistent criticisms of the reliability of dSph kinematics derived in this manner.

• Some early claims of large central velocity dispersions were based on spectra with single-epoch errors exceeding ~ 5-10 km s^-1. Most recent studies rely on spectra and reduction techniques that deliver single-epoch errors of 1-4 km s^-1 (Mateo et al 1991b;, Hargreaves et al 1994b, 1996b;, Olszewski et al 1995). These smaller errors have been confirmed from comparisons of results for common stars from independent studies (Hargreaves et al 1994b, 1996b;, Armandroff et al 1995;, Queloz et al 1995).

• The most luminous AGB stars are subject to atmospheric motions, or "jitter," with amplitudes of 2-10 km s^-1. Virtually all recent studies have pushed far below the upper tip of the RGB to luminosities where jitter is not seen in globular cluster red giants (Mateo et al 1991b, 1993;, Hargreaves et al 1994a, b, 1996b;, Queloz et al 1995;, Vogt et al 1995).

• Improved simulations of the effects of binaries have convincingly shown that, barring a pathological binary period distribution, dispersions based even on single-epoch observations are negligibly affected by binary motions (Hargreaves et al 1996a, Olszewski et al 1996a). The limited data available suggest that the binary frequency and period distribution are not radically different in dSph galaxies from what is seen in the solar neighborhood (Mateo et al 1991b;, Hargreaves et al 1994b, 1996b;, Olszewski et al 1995, 1996a;, Queloz et al 1995).

• In recent years, samples of over 90 stars have become available in many dSph galaxies (Armandroff et al 1995, Olszewski et al 1996a, Mateo 1997, Olszewski 1998). It is now possible to meaningfully measure departures from Gaussian distributions for such large samples (Merrifield & Kent 1990, Olszewski 1998) or construct velocity dispersion profiles within single galaxies (Mateo et al 1991b;, Da Costa 1994a;, Hargreaves 1994a, b, 1996b;, Armandroff et al 1995;, Mateo 1997).

These observational advances strongly suggest that modern measurements of the velocity dispersions of Local Group dSph galaxies are indeed reliable estimates of the true one-dimensional dispersions of these systems. I conclude that no dSph galaxy has a central velocity dispersion smaller than 6.6 km s^-1 (Table 7).

DIRR GALAXIES     Standard procedures exist to derive rotation curves for dIrr galaxies within and beyond the Local Group (Jobin & Carignan 1990, Puche et al 1990, 1991). However, only within the Local Group do we encounter dIrr galaxies whose kinematics are not dominated by rotation at all radii (Carignan et al 1990, 1991;, Lo et al 1993;, Young & Lo 1996a, 1997b). GR 8 exhibits rotation in its inner regions but then becomes pressure supported at large radii (Carignan et al 1990). The typical measure of the velocity dispersion in gas-rich but nonrotating dwarfs is from the 21-cm line width. Lo et al (1993) addressed this problem in detail; they recommended that where possible, the dispersion be based on the line-of-sight dispersion of the mean velocities of individual clouds. In practice, the two approaches seem to agree to within their combined errors.

7.2. Constraints on Dark Matter in Local Group Dwarfs

To determine masses and central mass densities of dSph galaxies, the King formalism is generally adopted (Richstone & Tremaine 1986), along with the simplifying assumptions that mass follows light and that the velocity dispersion is isotropic. Pryor & Kormendy (1990) have investigated the sensitivity of the derived masses for dSph galaxies on these and other assumptions. In general, the resulting M/L ratios for most dSph galaxies with good surface photometry are robust to within a factor of two (Pryor 1994, Mateo 1994, 1997). This same approach is also used to derive masses for pressure-supported dIrr systems (Lo et al 1993, Young & Lo 1997b). The rotation curves of the more luminous Local Group dIrr galaxies are typically fit with two-component models. One component of fixed M/L follows the visible-light or HI distribution; the second dark component is usually fit as an isothermal sphere to represent an extended dark halo. All of the Local Group dwarfs require both components for an adequate fit to the observed rotation curves. These techniques implicitly assume the galaxies are in dynamical equilibrium.

Figure 9 is a plot of the derived M/L ratios for all Local Group dwarfs with adequate data in Table 7. The King method (Richstone & Tremaine 1986) allows calculation of both the central density and total mass under the assumptions listed above. For the pressure-supported galaxies, plotting the central M/L ratio is therefore possible, while for all systems with kinematic data, the global M/L can be derived.

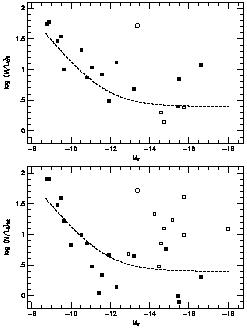
Figure 9. Kinematically determined mass-to-light ratios of local group dwarfs as a function of luminosity. Top panel: log (M/L)0 from Table 4 vs MV. Filled squares are for dSph or dSph/Irr systems for which masses were determined from the central velocity dispersions, while the open squares represent Irr systems that have masses derived here from HI rotation curves. See Table 4 for details or the original sources to obtain definitive kinematic mass estimates for these galaxies. Sagittarius is denoted as an open circle. Bottom panel: log (M / L)tot from Table 4 vs MV; the symbols are the same as in the top panel. In each panel I have also plotted the function log M / L = 2.5 + 107 / (L / L) as a dashed line.

The dIrr and early-type galaxies are clearly separated in the lower panel of Figure 9. This is not surprising: The dIrr systems all have masses constrained by rotation curves at large radii that can only be understood if the galaxies possess extended DM halos. For the early-type galaxies, the King formalism assumes that mass follows light. Hence, it is likely that the M/L ratios of all the early-type dwarfs are underestimated. Figure 9 also shows that the distribution of M/L ratios for the early-type dwarfs can be fit with the relation log M / L = 2.5 + 10⁷ / (L / L); these galaxies are consistent with the idea that each is embedded in a dark halo of fixed mass of about 10⁷ M and contains a luminous component with M/L_V = 2.5. This is a lower limit to the halo mass because the dark matter may plausibly be more extended than the luminous material.

Local Group dwarfs have proven useful to restriction of some possible forms of DM. For example, massive neutrinos have been ruled out in dSph galaxies from phase-space arguments (Lin & Faber 1983, Lake 1989a, Gerhard & Spergel 1992). Massive black-hole models (Strobel & Lake 1994) are also incompatible with the generally smooth central surface brightness distributions of the cores of dSph systems or the large global M/L ratios inferred in these systems (Demers et al 1995).

7.3. Alternatives to Dark Matter

The current fashion is to assume that the kinematic observations described above constitute part of a DM problem. However, it may be wise to remember that this already implies a solution to what remains a long-standing crisis in understanding the internal kinematics of galaxies. In this section, I discuss two possible alternatives to DM as they apply to Local Group dwarfs.

TIDES     Kuhn & Miller (1989), Kuhn (1993) proposed that one way to mimic the kinematic effects of DM was through a resonance process between the orbital period of a dwarf and its natural radial oscillation period. Pryor (1996), Olszewski (1998) reviewed recent studies that suggested that this mechanism is unlikely to have a significant effect on real dSph galaxies and for actual observational samples of stars used in kinematic studies. I add only two points here. First, tidal effects are indeed visible in many Local Group dwarfs (Section 8), but this alone does not imply that the central velocity dispersions, and hence the inferred mass-to-light ratios, are significantly affected until the galaxies are nearly completely disrupted. Second, the M/L ratios of isolated early-type galaxies such as LGS 3 and Leo II are sufficiently high to require DM, yet they are sufficiently far from any large galaxies that they cannot be affected significantly by tides. Kinematic studies of other isolated dwarfs such as Antlia and Tucana would be particularly helpful in settling this issue.

MODIFIED GRAVITY     Milgrom (1983a, b) introduced Modified Newtonian Dynamics, or MOND, to understand the rotation curves of disk galaxies (and some other related phenomena) with a modified form of Newton's law of gravity without resorting to DM. Only at very low accelerations (defined by the parameter a₀ ~ 2 x 10^-8 cm sec^-2) is Newton's law substantially altered from its standard form.

A single unambiguous example of a galaxy strictly obeying Newtonian dynamics in the low-acceleration regime would falsify MOND instantly. I do not address here how MOND currently fares with regard to understanding the dynamics of large galaxies apart from noting that no unambiguous failures have yet been reported (Sanders 1996, McGaugh & de Block 1998). Nor do I discuss the far-reaching implications of MOND on cosmology and other areas of astrophysics (Bekenstein & Milgrom 1984, Felton 1984, Sivaram 1994, Qiu et al 1995, Sanders 1997). Instead, I focus here on the use of Local Group dwarfs to test MOND.

Lake & Skillman (1989), Lake (1989b) suggested that the rotation curves of IC 1613 and NGC 3109 could not be explained by MOND unless a₀ 3 x 10^-9 cm sec^-2, a value that is incompatible with that needed to interpret rotation curves of giant systems. Milgrom (1991) noted that (a) MOND successfully fit the shapes of the rotations curves of these and other galaxies discussed by Lake (1989b) and (b) the mixed success that MOND had in reproducing the amplitudes of the rotation curves could be understood given the errors in the galaxy distances, inclinations, and asymmetric-drift corrections. For NGC 3109 (Jobin & Carignan 1990), Milgrom was in fact justified in claiming the earlier rotation curve was in error, though in the case of IC 1613, it remains unclear if Milgrom's objection to Lake & Skillman's (1989) conclusion is valid. More recently, Sanders (1996) found that the rotation curves of both NGC 55 and NGC 3109 are fit well by MOND.

Gerhard & Spergel (1992b) argued that the internal kinematics of Local Group dSph galaxies demanded DM even if MOND was used to estimate their masses. Lo et al (1993) found that the MOND masses for many nearby dIrr galaxies were smaller than their integrated HI masses - an obvious failure if correct. Milgrom (1995) responded that if the observational errors and most recent results were considered, neither effect claimed by Gerhard & Spergel (1992b) was observed. In the second case, Lo et al (1993) used an incorrect expression to determine the MOND masses, leading to estimates that were too small by a factor of 20 (Milgrom 1994). When the proper relation is used (M_MOND = 81₀⁴ / 4a₀ G, where ₀ is the observed central velocity dispersion for an isotropic system), the MOND masses are consistent with the inferred luminous (gaseous + stellar) masses without invoking a dark component.

The burden of proof remains squarely on MOND, but the kinematic data for Local Group dwarfs does not yet refute this alternative to DM.