3. GLOBAL ABUNDANCES AND YIELDS

We now have the tricky task of estimating the total heavy-element content of the universe. Considering stars alone, it seems reasonable to adopt solar Z as an average, but the total may be dominated by the still unseen intergalactic gas, which Mushotzky & Loewenstein argue to have the same composition as the hotter, denser gas seen in clusters of galaxies, i.e. about 1/3 solar. ⁽²⁾ It could be the case, though, that the metallicity of the IGM is substantially lower in light of the metallicity-density relation predicted by Cen & Ostriker (1999) and in that of the low metallicities found in low red-shift Ly- clouds by Shull et al (1998). Against this, we have neglected any metals contained in LSB galaxies or whatever makes up the shortfall between _IGM and _B, so we are being conservative in our estimate of _Z.

The mass of heavy elements in the universe is related to that of stars through the yield, defined as the mass of "metals" synthesised and ejected by a generation of stars divided by the mass left in form of long-lived stars or compact remnants (Searle & Sargent 1972). The yield may be predicted by a combination of an IMF with models of stellar yields as a function of mass, or deduced empirically by applying a galactic chemical evolution (GCE) model to a particular region like the solar neighbourhood and comparing with abundance data. E.g. 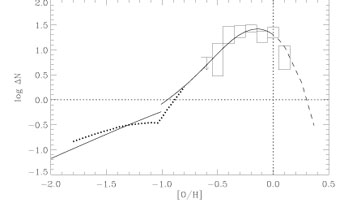Fig 1 shows an abundance distribution function for the solar neighbourhood plotted in a form where in generic GCE models the maximum of the curve gives the yield directly, and it is a bit below Z. Similar values are predicted theoretically using fairly steep IMFs like that of Scalo (1986). In Table 1, on the other hand, if we divide the mass of metals by the mass of stars, we get a substantially higher value, corresponding to a more top-heavy IMF.

Figure 1. Oxygen abundance distribution function in the solar neighbourhood, after Pagel & Tautvaisiene (1995).

There are two other indications for a top-heavy IMF, one local and one in clusters of galaxies themselves. The local one is an investigation by Scalo (1998) of open clusters in the Milky Way and the LMC, where he plots the IMF slopes found as a function of stellar mass. The scatter is large, but on average he finds a Salpeter slope above 0.7M and a virtually flat relation (in the sense dN / dlogm 0) below, which could quite easily account for the sort of yield found in Table 1. The other indication is just the converse of the argument we have already used in guessing the abundance in the IGM: the mass of iron in the intra-cluster gas is found (Arnaud et al 1992) to be

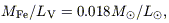
(1)

where L_V is the luminosity of E and S0 galaxies in the cluster. As has been pointed out by Renzini et al (1993) and Pagel (1997), given a mass:light ratio less than 10, we then have

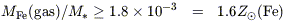
	(2)
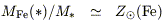
	(3)
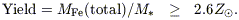
	(4)

The argument is very simple; the issue is just whether such high yields are universal or confined to elliptical galaxies in clusters.

² This refers to iron abundance, the relation of which to the more energetically relevant quantity Z is open to some doubt. Papers given at this conference indicate an SNIa-type mixture in the immediate surroundings of cD galaxies with maybe a more SNII-like mixture in the intra-cluster medium in general; for simplicity I assume the mixture to be solar. Back.