


HI redshift surveys have contributed substantially to our knowledge of the distribution of galaxies in the universe because of the advantages offered by 21-cm observations compared to optical surveys. Will this continue to be the case as future redshift surveys are carried out? The answer is a qualified 'no' (see also Vanden Bout & Haynes, this volume). Whereas radio telescopes, particularly Arecibo, had an advantage over optical surveys as long as (1) the latter were only observing one galaxy at a time and (2) the typical separation between galaxies was large compared to the HI beam size, neither condition will be true for surveys that probe deeper than galaxy catalogs like the CGCG. First, modern optical redshift surveys are being carried out using multi-object spectrographs which are capable of observing several dozen to a few hundred objects simultaneously. The multiplexing advantage makes optical surveys much more efficient. Second, the density of sources on the sky increases to the point where source confusion becomes a major problem for HI surveys. In addition, beam dilution significantly lowers the HI detection rate for higher redshift galaxies as their apparent diameters get smaller.
Does this mean that HI telescopes should get out of the redshift survey business? Not at all! Observations at 21-cm will still make an important contribution to our knowledge of the spatial distribution of galaxies. There are a number of areas where HI observations will remain not only viable, but dominant. As already indicated above, many of these areas are complementary to the optical survey work.
Of particular importance will be redshift work on LSB galaxies. Multi-object surveys like the LCRS routinely miss and/or ignore LSB galaxies because it is impossible to measure an optical redshift in a reasonable amount of time. The bias this places on studies of the spatial and luminosity distributions of galaxies could be severe. HI studies of LSB galaxies - both nearby dwarfs and distant LSB disk galaxies - will remain the best (and sometimes only) hope for getting redshifts for this relatively invisible but important population of galaxies. Likewise, galaxian surveys in the zone of avoidance and blind HI surveys will remain important applications of 21-cm observations.
One other significant role that HI observations can play in helping to develop our understanding of the distribution of matter in the universe is through the application of the Tully-Fisher (TF) relation. Rather than using redshifts to map out the 3D locations of galaxies, the TF relation allows us to assign distances that are independent of the observed recessional velocity. This in turn provides a measure of each galaxy's peculiar velocity - the difference between the observed redshift and the redshift predicted for an object at the true distance of the galaxy under the assumption of a uniform cosmic expansion. The peculiar velocity of a galaxy represents its line-of-sight motion due to local gravitational influences, and can be used to estimate the underlying mass distribution in the vicinity of the galaxy. In the following section, we highlight our recent work in applying HI and optical observations to the study of peculiar velocities in the local universe.
6.2. The All-sky Tully-Fisher Survey
Tully & Fisher (1977) proposed that the width of the HI emission profile, corrected for inclination, could be used as a predictor of galaxy luminosity, and thus, in comparison with the apparent brightness, a redshift-independent distance indicator. Motivated in part by the large database of HI widths available from the Arecibo redshift surveys, and in part by the sometimes confusing results obtained by early peculiar velocity studies, we decided to carry out our own TF study. Here we present an overview of the TF method, a brief summary of previous work, and a preliminary report of the results of our work.
Basis for the TF Relation The origin of this scaling relation has been discussed in various places (e.g., Aaronson & Mould 1986; Eisenstein & Loeb 1996), but it should be noted that the relation itself is derived empirically. Freeman (1970) has presented a classic discussion of the structure of the exponential disks characteristic of most spiral galaxies. In spirals, the disk component is generally expressed in terms of surface brightness (I) as a function of radius as I(r) = Io exp(-r/rd), where Io is the central surface brightness and rd is the disk scale length. Indeed, Freeman found that the central surface brightness is nearly constant in spirals, a characteristic commonly referred to as Freeman's Law. Its universality appears to be violated by a significant fraction of galaxies, especially ones characterized by much lower central surface brightness (e.g., Disney 1976; McGaugh 1996a). Nonetheless, the law does apply approximately to galaxies commonly found in existing catalogs, and plays an important role in a simple understanding of the origin of the TF scaling.
The total light emitted by an exponential disk is given by
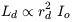
| (1) |
The mass interior to radius R is
M(R)  RV2. In the case
that the rotation curve flattens beyond some radius to some
Vmax, then the total mass in the disk is
RV2. In the case
that the rotation curve flattens beyond some radius to some
Vmax, then the total mass in the disk is
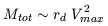
| (2) |
Combining equations (1) and (2), and performing some algebraic manipulation, we can write the total disk luminosity in terms of the mass-to-light ratio and the observables - the central surface brightness Io and the rotation curve maximum Vmax:
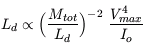
| (3) |
Allowing for the possibility that a dark matter halo contributes
significantly to the total mass, let us denote the fraction of the total
mass contained in the disk by
 , so that
Md =
, so that
Md =  Mtot. Then,
Mtot. Then,
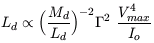
| (4) |
The TF scaling thus results from the simple assumptions that
the dark matter fraction and disk mass-to-light ratio are roughly constant
among spirals and that Freeman's law holds. In this case,
Ld  Vmax4,
similar in form both to the TF relation, and also to the analogous
relation for ellipticals,
L
Vmax4,
similar in form both to the TF relation, and also to the analogous
relation for ellipticals,
L 
 4, known as the
Faber-Jackson relation (where
4, known as the
Faber-Jackson relation (where
 is the stellar velocity
dispersion). In practice, none of these assumptions of constancy applies.
is the stellar velocity
dispersion). In practice, none of these assumptions of constancy applies.
 ,
Mtot / Ld and Io all
exhibit some mild dependence on scale (Vmax or
Ld), so that the scaling goes more like
Ld
,
Mtot / Ld and Io all
exhibit some mild dependence on scale (Vmax or
Ld), so that the scaling goes more like
Ld  Vmax
Vmax , where the value of
, where the value of
 satisfying most empirical TF
relations is in the range 3 - 3.5.
satisfying most empirical TF
relations is in the range 3 - 3.5.
Over the 20 years since the TF relation was first proposed as a distance indicator, much discussion has focused on the precise methodology. While the details of the relation lie beyond the scope of the current review, the interested reader is referred to the following references for a more thorough discussion: Strauss & Willick (1995), Giovanelli et al. (1994; 1996b, c).
Ingredients The TF relation is commonly used in the form MTF = a + b log Vmax. Most commonly, Vmax is equated to the observed 21-cm line profile width W, suitably corrected for observing aspect Wo = Wobs / sin i, redshift, and for the contributions of turbulence, signal-to-noise, and instrumental broadening. Imaging photometry using CCDs provides both the apparent magnitude m and the inclination, based on the observed disk ellipticity and an adopted intrinsic axial ratio. The TF relation can thus be used to derive redshift-independent distances from the combination of corrected line widths Wo and apparent magnitude m. The galaxy's peculiar velocity can then be calculated from the difference between the observed recessional velocity (corrected to some rest frame, e.g., the CMB) and the velocity expected for a galaxy at the TF-predicted distance.
Review of Peculiar Motion Results
The peculiar velocity of the Local Group has several distinct
components. As early as 1958, deVaucouleurs suggested that, since the
Virgo cluster represents a strong local density
enhancement, it should
induce a measurable infall velocity on the Local Group.
Models of the velocity field of the Local Supercluster
have been proposed by such authors as
Peebles (1976),
Schechter
(1980), and
Tonry & Davis
(1981).
Input parameters
generally include: (1) the infall velocity of the Local Group towards
Virgo, (2) the overdensity of Virgo relative to the
mean density, and (3) the exponent of the density falloff from Virgo, as
r- .
Early applications of the TF relation to the Local Supercluster
were presented by
Aaronson et
al. (1982).
Sandage (1986)
has pointed out that galaxies within
a few Mpc of the Local Group show no bulk motion with respect
to the Local Group. He concludes that, whatever peculiar velocity
is associated with the Local group, it is shared by all of the
galaxies within cz
.
Early applications of the TF relation to the Local Supercluster
were presented by
Aaronson et
al. (1982).
Sandage (1986)
has pointed out that galaxies within
a few Mpc of the Local Group show no bulk motion with respect
to the Local Group. He concludes that, whatever peculiar velocity
is associated with the Local group, it is shared by all of the
galaxies within cz  700 -
800 km s-1.
700 -
800 km s-1.
The recent COBE measurement (Kogut et al. 1993) confirms the previously recognized dipole anisotropy in the CMB of amplitude 3.3 ± 0.02 mK in the direction l, b = (265° ± 2°, +48° ± 2°). This is usually interpreted as a motion of the Local Group of amplitude 622 ± 20 km s-1 toward (lCMB, bCMB) = (277° ± 2°, +30° ±2°). It was noticed immediately that the motion of the Local Group with respect to the CMB points ~ 45° away from the direction to Virgo: a simple Virgo infall model does not agree with the magnitude or direction of the motion implied by the CMB dipole anisotropy. The discrepancy cannot be explained as being due to a rotation of the Local Supercluster.
Looking to explain the offset of the CMB apex from Virgo, Tammann & Sandage (1985) noted that the Hydra-Centaurus supercluster is located in the proper direction to contribute a component to the LG motion that, in addition to Virgo infall, might approach the CMB dipole velocity. In support of the importance of Hydra-Centaurus, Lilje et al. (1986) detected a shear in the local velocity field, with the expansion axis pointing toward the supercluster complex.
Soon thereafter,
Dressler et
al. (1987)
and Lynden-Bell et
al. (1988),
analyzing the motions of 300 elliptical galaxies derived from an application
of the Dn -
 relation, proposed a best
fit model that included
both Virgo infall and a component of motion of 570 km
s-1 toward a source
located at a distance of cz ~ 4350 km s-1 hidden
behind the southern
galactic plane which they dubbed the "Great Attractor" (GA). Since then,
much debate has focused on the validity of the GA model.
Strauss et
al. (1992),
using the results of an IRAS-selected redshift sample, place the
major perturber closer than 4500 km s-1, more in line with
the Hydra-Centaurus
distance. Other analyses of the IRAS galaxy distribution were presented
by Rowan-Robinson et
al. (1990)
and Scharf et
al. (1992).
The general conclusion which developed was that, while the local
velocity field is not just due to the Local Supercluster, the magnitude
of the
motion and its direction toward the purported GA is very uncertain.
relation, proposed a best
fit model that included
both Virgo infall and a component of motion of 570 km
s-1 toward a source
located at a distance of cz ~ 4350 km s-1 hidden
behind the southern
galactic plane which they dubbed the "Great Attractor" (GA). Since then,
much debate has focused on the validity of the GA model.
Strauss et
al. (1992),
using the results of an IRAS-selected redshift sample, place the
major perturber closer than 4500 km s-1, more in line with
the Hydra-Centaurus
distance. Other analyses of the IRAS galaxy distribution were presented
by Rowan-Robinson et
al. (1990)
and Scharf et
al. (1992).
The general conclusion which developed was that, while the local
velocity field is not just due to the Local Supercluster, the magnitude
of the
motion and its direction toward the purported GA is very uncertain.
Results even more challenging to current theories on the large-scale structure have been proposed. Scaramella et al. (1989; 1994) noticed a concentration of rich clusters near cz ~ 14,000 km s-1 in the general direction of the GA and postulated that infall into that overdense region may play a role. Willick (1990) found a bulk motion of the Pisces-Perseus supercluster in the general direction of Hydra-Centaurus, while Courteau et al. (1993) found general agreement with Willick's velocity field and suggested further that the entire local universe is in bulk flow in the general direction of Hydra-Centaurus. Using a photometric technique applied to brightest cluster ellipticals for 119 clusters, Lauer & Postman (1994) found that the clusters defined a reference frame that is in motion with respect to the CMB with an amplitude of 689 ± 168 km s-1 toward l = 343°, b = +52° (± 23°). A complete review of peculiar-motion studies is given by Dekel (1994).
The SFI Galaxy Survey If you are confused about the state of peculiar velocity measurements at this point, so were we and our colleagues. In order to try to better understand the situation, we decided to carry out our own study. As a result, our group has undertaken a homogenous, all-sky survey of a large sample of Sc galaxies with the objective of applying the TF relation to determine peculiar motions in the local universe. The sample, which we dub SFI, covers the sky north of -42° declination to a distance of VLG ~ 7500 km s-1, where VLG is the observed velocity measured relative to the centroid of the Local Group. In order to achieve a more even distribution in redshift and to reduce the contribution from low surface brightness and dwarf objects in the foreground, we applied a changing angular size selection criteria to our sample:
For VLG < 3000 km s-1, a
 2.0 arcmin. 2.0 arcmin.
|
For 3000 < VLG < 5000 km s-1, a
 1.6 arcmin. 1.6 arcmin.
|
For 5000 < VLG < 7500 km s-1, a
 1.3 arcmin. 1.3 arcmin.
|
The SFI survey combines I-band CCD imaging with high sensitivity 21-cm HI line observations and emphasizes uniform data processing and analysis. Our choice of Sbc-Sc galaxies aims to minimize possible type-dependent variations in fundamental parameters such as the mass-to-light ratio. We use the survey data to examine the effects on observed properties of viewing aspect, internal extinction, and local environment. Careful sample definition, large sample size and uniform coverage both on the sky and with redshift allows analysis of Malmquist and selection bias, completeness, and statistical uncertainties for comparison with models and reconstruction of the density field.
After beginning the project, the importance of deriving an accurate TF
template relation became apparent to us, and thus a second project,
dubbed the Cornell-Arecibo-Palomar clusters project, was undertaken.
For HI-deficient galaxies in cluster cores, for which HI velocity
widths are therefore unattainable, we derived a complementary measure
of rotational velocity from
H rotation curves obtained
with the Palomar 5-m telescope. Our sample consists of 798 galaxies
within and near 24 distant clusters (the SCI sample). After applying
strict membership criteria based on available redshift data, and
following the iterative technique described in
Giovanelli et
al. (1996b),
a template TF relation was derived using 351 galaxies. Our final cluster
member TF template is shown in Figure 7.
rotation curves obtained
with the Palomar 5-m telescope. Our sample consists of 798 galaxies
within and near 24 distant clusters (the SCI sample). After applying
strict membership criteria based on available redshift data, and
following the iterative technique described in
Giovanelli et
al. (1996b),
a template TF relation was derived using 351 galaxies. Our final cluster
member TF template is shown in Figure 7.
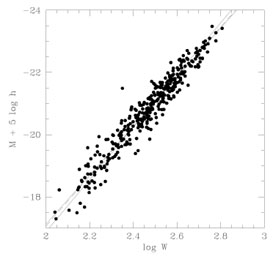
|
Figure 7. Template I-band Tully-Fisher relation for 351 galaxies located in 24 clusters. Lines indicate the fits to the direct, inverse, and bi-error TF relations. See Giovanelli et al. (1996b) for details. |
Results from the SFI Sample
The results from the SFI sample are being published in a series of papers
(Giovanelli et
al. 1994;
1995;
1996a,
b,
c;
Freudling et
al. 1995;
da Costa et
al. 1996).
First of all, we emphasize that there are many
subtleties in the application of the TF technique that can lead to
spurious results. An inadequate TF template relation can easily simulate
bulks flows or other geocentric features of the velocity field. Incorrect
internal extinction laws have produced inclination-dependent peculiar
velocities, increased the inferred scatter in the TF relation, and
altered its slope (because of a residual dependence
of extinction on galaxy luminosity
[Giovanelli et
al. 1995;
see also
Willick et
al. 1996]).
Because it was not realized that
the main source of the observed scatter in the TF relation is the error in
the velocity width and that the error depends on W, corrections for scatter
in the TF relation, dubbed the "homogeneous Malmquist bias", have
often been inadequate. Often, published global 21-cm line widths,
including many we reported in past redshift surveys, were heavily smoothed,
and thus artificially broadened. Adequate corrections for smoothing,
instrumental broadening and signal-to-noise are required. It is also
apparent that the TF relation becomes unreliable for small width galaxies,
partly because errors dominate
( W / W large),
and partly because turbulent
motions contribute a significant, but uncertain, component of the velocity.
Other omissions include the failure to correct for the effect of redshift
cutoff in the sample, which produces spurious peculiar velocities in the
outer shells of the sample volume. For all these reasons, application of
the TF method to derive peculiar velocities is a tricky business; lots
of things can, and probably do, go wrong.
W / W large),
and partly because turbulent
motions contribute a significant, but uncertain, component of the velocity.
Other omissions include the failure to correct for the effect of redshift
cutoff in the sample, which produces spurious peculiar velocities in the
outer shells of the sample volume. For all these reasons, application of
the TF method to derive peculiar velocities is a tricky business; lots
of things can, and probably do, go wrong.
Our analysis of the SFI sample to derive peculiar velocities has incorporated our own data to derive the various corrections mentioned in the preceding paragraph and to estimate errors using both empirical analysis and Monte Carlo simulations.
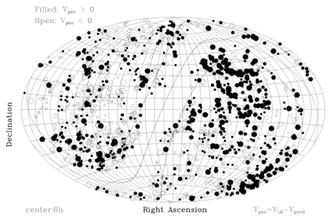
|
Figure 8. Map of the peculiar velocities of 1585 Sc galaxies from the SFI project. The map coordinates are the same as in Figure 1. Galaxies with positive Vpec (motion away) are plotted as filled symbols, while those with negative Vpec (motion toward us) are open symbols. The size of the symbol is proportional to the magnitude of the peculiar velocity. In this figure, Vpec is measured relative to the rest frame of the Local Group. Note the strong dipole signature between the north and south galactic caps: galaxies in the south are preferentially moving away, while those in the north are moving toward us. |
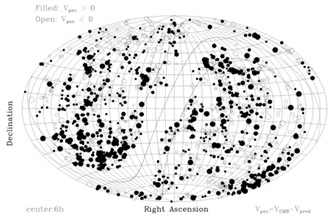
|
Figure 9. The same as Figure 8, except that now Vpec is measured relative to the rest frame defined by the cosmic microwave background. The dipole signature has disappeared. The concentration of filled symbols on either side of the zone of avoidance in the southern portion of the sky represents the infall into the Hydra-Centaurus supercluster (a.k.a. the Great Attractor). |
In general, the peculiar velocities derived from the SFI and cluster samples are smaller than those found by others. Figures 8 and 9 present the visual comparison of our results for the so-called convergence depth, the volume which contains the mass responsible for our motion with respect to the CMB. Figure 8 shows the distribution on the sky of the peculiar velocities derived from the SFI sample. The symbol size reflects the amplitude of the peculiar velocity: filled circles represent positive peculiar velocities, while open ones show negative peculiar velocities. Thin lines denote the galactic plane and lines of constant latitude b = ±20°. In this figure, velocities are referenced to the rest frame of the Local Group: Vpec = VLG - VTF. For comparison, Figure 9 shows the corresponding diagram, but now referencing the peculiar velocities to the rest frame of the CMB: Vpec = VCMB - VTF. A comparison of the two figures reveals that the dipole distribution evident in Figure 8 disappears in Figure 9. Thus, we conclude that the dipole motion inferred from the CMB observations is the dominant feature seen in maps of peculiar velocity referenced to the Local Group. The result is quantified in Table 2 which shows the dipole amplitude and direction derived from analysis of the sample in separate shells of redshift. As the sample is divided into redshift shells, both the apex and the amplitude of the motion converge toward that implied by the CMB dipole anisotropy (Kogut et al. 1993). Thus, the "convergence depth" is on the order of 6000 km s-1.
| Vcmb Window | Vpec(LG) | l | b | #Gals. |
| All | 417±28 | 253±9 | 37±3 | 1585 |
| 2000-3000 km s-1 | 333±41 | 268±16 | 41±8 | 235 |
| 3000-4000 km s-1 | 437±57 | 242±20 | 24±5 | 303 |
| 4000-5000 km s-1 | 551±62 | 236±24 | 37±5 | 372 |
| 5000-6000 km s-1 | 566±81 | 281±15 | 24±25 | 270 |
| CMB | 627±22 | 276±3 | 30±3 | |
Examination of Table 2 shows that the region enclosed within a 6000 km s-1 radius of the Local Group exhibits a mild bulk flow of order 200 km s-1. However, this bulk flow results from the asymmetry of the mass distribution within that volume and, in particular, the location of the Local Group in a region characterized by a large gradient in the mass density. The density field reconstructed from the observed velocity field agrees well with ones derived from redshift surveys; the known major supercluster complexes are recovered. This reconstruction, presented in da Costa et al. (1996), emphasizes the reality of voids as truly underdense regions. Using the SFI sample, Giovanelli et al. (1996a) have addressed the large-scale bulk flow model of Lauer & Postman (1994, LP) by adding in opposition the velocities of 250 galaxies in each of the cones in the apex and antapex direction of the LP bulk flow. Comparing in windows of CMB radial velocity in order to avoid complications of the Malmquist bias corrections, we find that the SFI galaxies reveal a significant component of bulk flow along the LP apex-antapex direction, but with a smaller amplitude. However, the motion appears to die down at distance shells beyond 6000 km s-1. Either there is a direct conflict with the LP bulk motion, or the geometry of the mass distribution in the local universe is such that the peculiar velocity field locally (cz < 7000 km s-1) is quiescent and surrounded by a concentric outer shell moving at high velocity with respect to this inner region.