2. THE EGRB FROM 0.03 TO 10 GEV

The most promising model proposed for the origin of the GeV range extragalactic -ray background (EGRB), first detected by SAS-2 and later confirmed by EGRET [1], is that it is the collective emission of an isotropic distribution of faint, unresolved blazars (See Ref. [7] and references therein.). Such unresolved blazars are a natural candidate for explaining the EGRB since, they are the only significant non-burst sources of high energy extragalactic -rays detected by EGRET.

2.1. The Unresolved Blazar Model:

To determine the collective output of all -ray blazars, one can use the observed EGRET distribution of -ray luminosities and extrapolate to obtain a "direct" -ray luminosity function (LF) per comoving volume, f(l, z) [8]. Alternatively, one can make use of much larger catalogs at other wavelengths and assume a relationship between the source luminosities at the catalog wavelength and the GeV region [9], [10]. Both methods have uncertainties.

With regard to the former method, only the "tip of the iceberg" of the -ray LF has been observed by EGRET. Lower luminosity -ray sources whose fluxes at Earth would fall below EGRET's minimum detectable flux, i.e. EGRET's point source sensitivity (PSS), are not detected. Extrapolating the -ray LF to fainter source luminosities must then involve some extra assumption or assumptions.

We have chosen to use the latter method and have assumed a linear relation between the luminosities of a source at radio and -ray wavelengths in an attempt to estimate a LF which would hold at fainter luminosities. The extent of such a correlation is by no means well established [10] - [12]. However, since most theoretical models invoke the same high energy electrons as the source of both the radio and -ray emission, a quasi-linear relation between radio and -ray luminosities is a logical assumption. In fact, recent observations support this supposition [13].

We used this latter method to estimate the contribution of unresolved blazars to the EGRB, and found that up to 100% of the EGRB measured by can be accounted for [7]. Our model assumes a linear relationship between the differential -ray luminosity l at E_f = 0.1 GeV and the differential radio luminosity l_r at 2.7 GHz for all sources, l l_r with determined by the observational data. One can then used the measured radio LF f_r(l_r, z) for blazars (flat spectrum radio sources) [14] to calculate the collective -ray output of all blazars. This LF is shown in Figure 2.

Figure 2. Radio luminosity (power) function at 2.7 GHz after Dunlop and Peacock [14].

The simplified elements of our calculations are as follows: We assume that blazars spend 97% of their time in a quiescent state and the remaining 3% of their time in a flaring state We assume that the -ray and radio LFs in their quiescent state are related by f(l, z) = ^-1 f_r(^-l , z). This relation changes by an average -ray "amplification factor", < A > = 5, when the blazars are flaring. We assume that -ray spectra for all sources are of the power-law form l(E) = l(E / E_f)^-, where is assumed to be independent of redshift. We have taken the distribution of such spectral indeces, , from appropriately related EGRET data. We also assume a slight hardening of the blazar spectra when they are in the flaring state which is supported by the EGRET data. For further details, see Ref. [7].

The number of sources N detected is a function of the detector's PSS at the fiducial energy E_f, [F(E_f)]_min, where the integral -ray photon flux F is related to l by

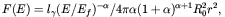
(2)

where R₀ r(1 + z) is the luminosity distance to the source. The number of sources at redshift z seen at Earth with an integral flux F(E_f) is given by

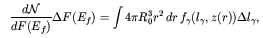
(3)

where l in the integrand depends on z(r) and F(E_f) from eq. 2. The LF, f, includes both quiescent and flaring terms. Figure 3 shows the results of our calculation of the number of sources versus flux above 0.1 GeV, i.e., our predicted source count curve, compared to the EGRET detections [7]. The cutoff at ~ 10^-7 cm^-2 s^-1 for E_f = 0.1 GeV, their quoted PSS, is evident by the dropoff in the detected source count below this flux level.

Figure 3. Source number count per one-fifth decade of integral flux at Earth The straight dotted line is the Euclidean relation N(> F) F-3/2 for homogeneous distribution of sources . The open circles represent the EGRET blazar detections and the solid line is the model prediction.

To calculate the EGRB, we integrate over all sources not detectable by the telescope to obtain the differential number flux of EGRB photons at an observed energy E₀:

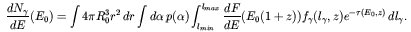
(4)

This expression includes an integration over the probability distribution of spectral indices based on the second EGRET Catalog [15].

There is also an important attenuation factor in this expression; the attenuation occurring as the -rays produced by blazars propagate through intergalactic space and interact with cosmic UV, optical, and IR background photons to produce e^± pairs. If a substantial fraction of the EGRB is from high-z sources, a steepening in the spectrum should be seen at energies above ~ 20 GeV caused by the attenuation effect [16]. Figure 4, from Ref. [16], shows the calculated EGRB spectrum (based on the EGRET PSS) compared to EGRET data. The slight curvature in the spectrum below 10 GeV is caused by the distribution of unresolved blazar spectral indeces; the harder sources dominate the higher energy EGRB and the softer sources dominate the lower energy EGRB. The steepened spectra above ~ 20 GeV in Figure 4 show the attenuation effect and its uncertainty.

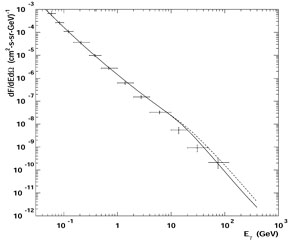
Figure 4. The predicted EGRET EGRB from unresolved blazars compared with the EGRET data. GLAST should see an EGRB about a factor of 2 lower at energies above 1 GeV (see text).

2.2. Critique of the Assumption of Independence of Blazar Gamma-Ray and Radio Luminosities

Chiang and Mukherjee [17] have attempted to calculate the EGRB from unresolved blazars assuming complete independence between blazar -ray and radio luminosities. They then used the intersection between the sets of flat spectrum radio sources (FSRSs) of fluxes above 1 Jy found in the Kühr catalogue and the blazars observed by EGRET as their sample, optimizing to the redshift distribution of that intersection set to obtain a LF and source redshift evolution. Using this procedure, they derived a LF which had a low-end cutoff at 10⁴⁶ erg s^-1. Then, with no fainter sources included in their analysis, they concluded that only ~ 1/4 of the 0.1 to 10 GeV EGRB could be accounted for as unresolved blazars and that another origin must be found for the EGRB in this energy range.

We have argued above that it is reasonable to expect that the radio and -ray luminosities of blazars are correlated. Any such correlation will destroy the assumption of statisitical independence made by Chiang and Mukherjee and introduce a bias in their analysis. In fact, their analysis leads to many inconsistencies. Among them are the following:

A. The LF derived by Chiang and Mukherjee [17] allows for no sources with luminosities below 10⁴⁶ erg s^-1. In fact, all of the six sources found by EGRET at redshifts below ~ 0.2 have luminosites between ~ 10⁴⁵ erg s^-1 and ~ 10⁴⁶ erg s^-1 [18]. Elimination of fainter sources from the analysis can only lead to a lower limit on the EGRB from unresolved blazars. The fainter sources contribute significantly in acounting for unresolved blazars being the dominant component of the EGRB. (In this regard, see also, Ref. [19])

B. Chiang and Mukherjee limit the EGRET sources in their analysis only to the FSRSs in the Kühr catalogue. However, if there is truly no correlation between blazar radio and -ray luminosities, then any of the millions of FSRSs given by the Dunlop and Peacock radio LF [14] are equally likely to be EGRET sources. In that case, of the 50 odd sources in the 2nd EGRET catalogue, virtually none, i.e. ~ 10^-6, should be Kühr sources.

The above discussion indicates that the assumption of non-correlation between the radio and -ray fluxes of blazars made by Chiang and Mukherjee in their analysis is not a good one and that this assumption invalidates their conclusions.

2.3. GLAST and the EGRB:

With an estimated point source sensitivity (PSS) nearly two orders of magnitude lower than EGRET's, GLAST will be able to detect O(10²) times more blazars than EGRET, and measure the EGRB spectrum to > 1 TeV (assuming the EGRET power law spectrum). These two capabilities will enable GLAST to either strongly support or reject the unresolved-blazar hypothesis for the origin of the EGRB.

Figure 3 shows that O(10³) blazars should be detectable by GLAST, assuming it achieves a PSS of ~ 2 × 10^-9 cm^-2 s^-1. Using this PSS and our derived source count curve as shown in Figure 3, we have estimated that the remaining "diffuse" EGRB seen by GLAST should be a factor of ~ 2 lower for E > 1 GeV. Below 1 GeV, this factor of 2 will not apply because source confusion owing to the poorer angular resolution of GLAST at these lower energies will reduce the number of blazars resolved out of the background.

We conclude that GLAST can test the unresolved blazar background model in three ways:

A. GLAST should see roughly 2 orders of magnitude more blazars than EGRET because of its ability to detect the fainter blazars which contribute to the EGRB in our model. It can thus make a much deeper determination of the source count curve. GLAST can also determine the redshift distribution of many more identified -ray blazars, using its better point source angular resolution to make identifications with optical sources having measured redshifts. With its larger dynamic range, GLAST can then test the assumption of an average linear relation between the -ray and radio fluxes of identified blazars. All of these determinations will test the basic assumptions and results of our model.

B. With its better PSS, GLAST will resolve out more blazars from the background. Thus, fewer unresolved blazars will be left to contribute to the EGRB. reducing the level of the measured EGRB compared to EGRET's by a factor of ~ 2 if our predictions are correct.

C. The much greater aperture of GLAST at 100 GeV will allow a determination of whether or not a steepening exists in the EGRB, since the number of EGRB -rays recorded by GLAST above 100 GeV will be of order 10³ to 10⁴, assuming a continuation of the EGRET power-law spectrum. Such a steepening can be caused by both absorption and intrinsic turnovers in blazar spectra. Given enough sub-TeV spectra of individual blazars with known redshifts, these two effects can be separated.