2. OBSERVATIONS

2.1. A brief history

The history of the measurement of distances using globular clusters can be broken into four eras.

The measurement of the brightest globular clusters in M87 by Baum (1955) and Racine (1968) launched the first era. Ironically, given the recent history of the distance scale question, Sandage (1968) found H₀ = 75 km s^-1 Mpc^-1 using the first-ranked globular cluster in M87 while de Vaucouleurs (1970) found H₀ = 50 km s^-1 Mpc^-1. It was clearly recognized that size-of-sample effects introduced large uncertainties in these estimates.

During the 70s, deeper photographic observations allowed comparisons of the bright side of the luminosity function (e.g. Hanes 1977, 20 galaxies in the Virgo cluster down to V 21.6 mag; Strom et al. 1981, 1700 clusters in M87 to B 23.5 mag), eventually leading to the development of sophisticated maximum-likelihood techniques for comparing distributions (e.g. Hanes & Whittaker 1987, Seeker & Harris 1993). While this dramatically improved the accuracy (in fact Hanes & Whittaker argue that "there is no need to strive for much deeper levels"), the results were still sensitive to the unknown width of the distribution which was not well constrained by the data.

The availability of CCD detectors in the 80's opened the third era, with the number of measured GCLF increasing rapidly (e.g. van den Bergh, Pritchet, & Grillmair 1985, Bridges, Hanes, & Harris 1991, Harris et al. 1991, Ajhar, Blakeslee, & Tonry 1994, Blakeslee & Tonry 1996, Kohle et al. 1996). Some of these observations reached the turnover or just past the turnover, providing more secure measurements by allowing a determination of the peak of the distribution.

The faint limiting magnitude of the Hubble Space Telescope now makes it possible to routinely reach two or three magnitudes beyond the turnover at the distance of the Virgo cluster (e.g. Whitmore et al. 1995, Elson & Santiago 1996a, b, Forbes 1996a, b), hence opening the fourth era. Even the Coma cluster is within our reach, although only barely if we wish to reach past the peak of the luminosity function (Baum et al. 1995). The primary improvements that can be expected from HST observations are; more accurate determinations of the peak and width of the GCLF, higher precision color measurements which may be necessary for separating red (metal rich) and blue (metal poor) clusters, the opportunity to increase the number of local calibrators using HST observations of Cepheids in galaxies as distant as the Virgo and Fornax clusters, and a determination of the degree to which the GCLF is universal.

2.2. HST observations

The Hubble Space Telescope (HST) provides several advantages over ground-based telescopes for measuring the GCLF. The first is the ability to reach more than two magnitudes past the turnover for single orbit observations in the Virgo cluster. Another important advantage is the ability to differentiate the globular clusters, which are barely resolved at the distance of the Virgo cluster, from both foreground stars and background galaxies. Finally, the excellent spatial resolution makes it possible to use very small apertures which reduces the effect of the galaxy background, resulting in higher precision observations right into the core of the galaxy where the density of clusters is highest. Figure 1 shows an example of an HST image of a portion of M87 (Whitmore et al. 1995). The large improvement over the ground-based observations (i.e. the objects labeled "C" from Couture, Harris, & Allwright 1990) is readily apparent.

Figure 1. A portion of the M87 field from Whitmore et al. (1995) showing how much deeper HST observations are compared to ground-based. The objects labeled "C" are from the ground-based observations of Couture et al. (1990). The squares show clusters with luminosities near the peak of the luminosity function while the circles show clusters roughly 1.5 mag past the peak.

It is interesting that the first study using HST observations to attempt to determine the Hubble constant using the GC's was the most difficult to date. Baum et al. (1995) attempted to measure the turnover in the GCLF for the non-central elliptical galaxy NGC 4881 in the Coma cluster, with a distance modulus roughly 3.7 magnitudes fainter than the Virgo cluster. They were unable to see any turnover in the distribution, and therefore only quote an upper limit for the Hubble constant of H₀ = 67 (+7, -67) km s^-1 Mpc^-1. However, this is somewhat misleading since they clearly see the bright end of the distribution, so very low values of H₀ are not possible. If we assume a GCLF similar to M87 (Whitmore et al. 1995), a value of M⁰_V = -7.21 mag (Section 3.1), and use the bright half of the distribution to estimate the total number of clusters, we find the value of m_V at 5% of the distribution yields a positive detection of H₀ = 72 ± 13 km s^-1 Mpc^-1, rather than an upper limit. It is not unexpected that the turnover was not seen, since the 50% detection threshold was at m_V = 27.3 mag while the peak is predicted at a value m⁰_V 27.8 mag for this value of H₀. In addition, the observations were made before the WFPC2 was cooled, hence the number of hot pixels is very large. While Baum et al. attempt to take these limitations into account, the observations are clearly pushing the limit of this particular dataset. It should be possible to observe roughly one magnitude deeper by using the WFPC2 after the cooldown and by using spatial dithering to flatten the background and remove hot pixels.

The HST observations of M87 by Whitmore et al. (1995) reached more than 2 magnitudes beyond the turnover of the GCLF. With over 1000 clusters in the sample this currently represents the best GCLF available for any galaxy, providing statistical accuracies roughly a factor of two smaller than any previously measured galaxy, including the Milky Way and M31 which have much smaller populations. A Gaussian profile with m⁰_V = 23.72 ± 0.06 mag and = 1.40 ± 0.06 mag provide a good fit to the data, leading to an estimate for the Hubble constant of H₀ = 78 ± 11 km s^-1 Mpc^-1. The color distribution is strongly bimodal, with peaks near V - I = 0.95 mag and 1.20 mag. This raises the question of whether the red and blue clusters have the same value of M⁰_V.

Elson & Santiago (1996a, b) observed fields in M87 roughly 2.5' from the center. Although their samples are smaller (146 and 220 clusters), their results are consistent with those of Whitmore et al. (1995). In particular, Elson & Santiago (1996b) find a bimodal color distribution with even sharper peaks at V - I = 0.92 mag and 1.23 mag. They find that the red clusters are roughly 0.3 magnitudes fainter than the blue clusters (see Section 3.2.3 for a discussion).

Forbes et al. (1996) and Forbes (1996a, b) have used HST to study GCs in 14 elliptical galaxies with kinematically-distinct cores. The GCLF of three galaxies (NGC 4365 in either the Virgo cluster or possibly the Virgo W' cloud, and NGC 4278 and NGC 4494 in the Coma I Cloud) have been determined and used to produce estimates of the Hubble constant in the range 72 - 80 km s^-1 Mpc^-1. However, questions concerning membership and peculiar velocities of these clouds limit the reliability of these estimates.

Whitmore et al. (1996), as part of their study of candidate young and intermediate-age globular clusters in merger remnants, find that the old, metal-poor population of globular clusters in most galaxies have remarkably constant colors with mean values of V - I = 0.95 mag (i.e. the Milky Way, M31, ellipticals with narrow color distributions, the blue peak of ellipticals with bimodal color distributions, and the old populations in merger remnants). Following the suggestion by Zepf and Ashman (1993), they argue that the red clusters found in some ellipticals (e.g. M87) are metal-rich GC's formed in a second episode of cluster formation, presumably during a merger event. This may be important for distance measurements since red and blue clusters may have slightly different values of M⁰_V. They also find that the bright wing of the GCLF for five galaxies observed with HST is remarkably constant, with a scatter of just 0.1 mag, indicating that fairly good distance estimates can be determined as long as the completion limit reaches m_V -8 mag. This is similar to the conclusion of Hanes & Whittaker (1987). For HST, with a limiting magnitude around m_V = 29 mag, this implies a distance modulus of 37 mag and a distance of 250 Mpc. Elson, Santiago, & Gilmore (1996) have shown that globular clusters can be seen out to a distance modulus of 39 mag in the Hubble Deep Field.

2.3. A compilation and estimate of the intrinsic dispersion in M⁰_V

A Gaussian distribution provides a good representation of the GCLF for most galaxies when plotted in magnitude bins (e.g. Hanes 1977, Harris 1991, Jacoby et al. 1992; however, see Secker 1992, and Kissler et al. 1994, who argue that a t distribution with a shape parameter µ = 5 is a slightly better fit to the Milky Way and M31 GCLFs). Figure 2 shows the data for M87 from Whitmore et al. (1995; see also Figure 7 in Jacoby et al. 1992). The two primary quantities that will be compiled are, m⁰_V, the extinction corrected apparent magnitude of the turnover of the GCLF in the Johnson V passband, and , the standard deviation or "width" of the distribution.

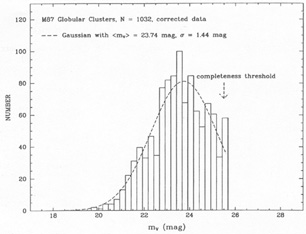
Figure 2. The GCLF for M87 from Whitmore et al. (1995) showing that a Gaussian profile provides a good fit.

Tables 1 and 2 provide a compilation of m⁰_V and for 18 giant elliptical galaxies deemed of high enough quality to provide estimates with uncertainties less than about 0.3 mag. See H96 for a compilation of GCLFs for spirals and dwarf galaxies, and a plot of M⁰_V vs. galaxy, luminosity. Table 1 shows that m⁰_V (and therefore M⁰_V) is remarkably constant, with a raw scatter of 0.21 mag for the Virgo cluster (0.24 mag if NGC 4365 and NGC 4636 are included), and 0.18 in the Fornax cluster.

Table 1. m⁰_V and a for elliptical galaxies in the Virgo and Fornax clusters

	m0V	±		±	Reference
Fornax Cluster
NGC 1344	23.80	0.25 mag	1.35	0.18 mag	Blakeslee & Tonry (1996)
NGC 1374	23.52	0.14	-	-	Kohle et al. (1996)
NGC 1379	23.68	0.28	-	-	Kohle et al. (1996)
NGC 1380	24.05	0.25	1.30	0.17	Blakeslee & Tonry (1996)
NGC 1399	23.81	0.09	-	-	*** weighted mean ***
"	23.90	0.08	-	-	Kohle et al. (1996)
"	23.83	0.15	1.38	0.09	Blakeslee & Tonry (1996)
"	23.85	0.30	(1.4)	-	Bridges et al. (1991)
"	23.45	0.16	1.20	-	Geisler & Forte (1990)
"	24.00	0.20	-	-	Madejsky & Bender (1990)
NGC 1404	24.01	0.14	-	-	*** weighted mean ***
"	24.10	0.20	(1.4)	-	Richtler et al. (1992)
"	23.92	0.20	1.32	0.14	Blakeslee & Tonry (1996)
NGC 1427	23.78	0.21	-	-	Kohle et al. (1996)
weighted mean: (n = 7)	23.80 mag ± 0.18 (scatter) ± 0.07 (m.e.)
Virgo Cluster
NGC 4374	24.12	0.3	(1.4)	-	Ajhar et al. (1994)
NGC 4406	24.25	0.3	(1.4)	-	Ajhar et al. (1994)
NGC 4472	23.85	0.08	-	-	*** weighted mean ***
"	23.84	0.11	(1.46)	-	Harris et al. (1991)
"	23.72	0.3	(1.4)	-	Ajhar et al. (1994)
"	23.99	0.3	1.20	-	Cohen (1988)
NGC 4486	23.88	0.07	-	-	*** weighted mean ***
"	23.73	0.06	1.40	0.06	Whitmore et al. (1995)
"	24.14	0.30	-	-	van den bergh et al. (1985)
"	23.99	0.3	1.50	-	Cohen (1988)
"	23.74	0.3	(1.4)	-	Elson & Santiago (1996a)
"	23.99	0.3	1.57	-	Bison & Santiago (1996b)
"	24.20	0.3	1.73	-	McLaughlin et al. (1994)
"	23.92	0.13	(1.46)	-	Harris et al. (1991)
NGC 4552	23.70	0.3	(1.4)	-	Ajhar et al. (1994)
NGC 4649	23.79	0.14	(1.46)	-	Harris et al. (1991)
weighted mean: (n=6)	23.89 mag ± 0.21 (scatter) ± 0.09 (m.e.)

Table 2. m⁰_V and for other elliptical galaxies

	m0V	±		±	Reference
Leo Group
NGC 3377/79	22.55	0.40 mag	(1.2 mag)	-	Harris (1990)
NGC 3379	22.20	0.30	-	-	Pritchet et al. (1985)
Coma Group
NGC 4278	23.23	0.11	1.21	0.09	Forbes (1996a)
NGC 4494	23.05	0.13	1.09	0.11	Forbes (1996a)
"	23.65	0.40	1.4	0.11	Fleming et al. (1995)
Possible Virgo Cluster
NGC 4365	24.37	0.15	-	-	*** weighted average ***
"	24.20	0.30	1.28	0.15	Forbes (1996a)
"	24.29	0.18	(1.46)	-	Harris et al. (1991)
"	24.68	0.3	(1.4)	-	Ajhar et al. (1994)
NGC 4636	24.18	0.20	-	-	Kissler et al. (1994)
NOTES TO TABLES 1 AND 2
(a) Values of m0V have been corrected to AV = 0.06 mag for the Virgo Cluster, based on the average for the galaxies in this sample from Burstein & Heiles (1984). The mean for Fornax was negative, so a value of AV = 0.00 mag has been used, as recommended by Burstein & Heiles.
(b) If no error estimate has been made for m0V, a value of 0.3 is assumed in order to compute the weighted mean.
(c) Values of in parenthesis indicate cases where an assumed rather than derived value has been used.
(d) A value of V - R = 0.5 mag has been used to convert value of MR from Ajhar et al. (1994).
(e) A value of B - V = 0.8 mag has been used to convert value of MB from Harris et al. (1991), and van den Bergh et al. (1985).
(f) A value of V - g = -0.15 mag has been used to convert value of Mg from Cohen (1988).
(g) A ratio of 2/1 for the blue/red clusters has been used to calculate the total values from Elson & Santiago (1996b).
(h) Alternative estimates of m0V for the Harris et al. (1991) data, based on maximum likelihood techniques, are available in Secker & Harris (1993).

Part of the observed dispersion is due to measurement uncertainties. Using galaxies with repeat measurements shows that a typical measurement error is 0.16 mag. Another source of uncertainty is the size of the cluster, with some galaxies in the front or back of the cluster. This is especially important for the Virgo cluster due to its large extent. Assuming the Virgo cluster can be modeled as a sphere with 30 radius, and the more compact Fornax cluster with a 10 radius, leads to uncertainties of 0.11 mag (Virgo) and 0.04 mag (Fornax). Subtracting the measurement uncertainty and depth of cluster uncertainty in quadrature (after taking into account the galaxies with multiple measurements) leaves estimates for the intrinsic dispersion of 0.13 mag (Virgo) and 0.11 mag (Fornax). These values compare well with even the best distance estimators (e.g. Cepheids with 0.10 mag dispersion, Jacoby et al. 1992). The intrinsic dispersion may be even smaller if it turns out that red and blue clusters have slightly different values of M⁰_V (see Ashman, Conti, & Zepf 1995 and Elson & Santiago 1996b), requiring a small correction depending on the ratio of red-to-blue clusters.

Using the measured rather than assumed values from Table 1 and 2 leads to a mean value of = 1.35 ± 0.05 mag, with a scatter of 0.17 mag (NOTE: error estimates derived in this review are 1 sigma uncertainty in the mean, taking external errors into account when applicable; e.g. values of M⁰_V include the uncertainty in the Cepheid zeropoint). If we restrict the sample to the nine cases where error estimates have been made we find an observed scatter of only 0.10 mag, smaller than the mean predicted uncertainty of 0.12 mag. It may therefore be best to assume a fixed value of when estimating m⁰_V, since there is little evidence at present for any real scatter in . The near constancy in M⁰_V and explains why reasonably good distance determinations can be made using just the bright part of the GCLF (Hanes & Whittaker 1987, Whitmore et al. 1996). It should be noted, however, that spiral galaxies appear to have values of which are roughly 0.2 mag lower (H96).