


3.5. Sizes and Structures of Clusters
Sizes of clusters are difficult to determine because (a) the boundary between a cluster and the field is indefinite, and (b) usually only the brighter cluster members are observed whereas if the cluster has approached a state of statistical equilibrium the fainter unseen members should be more broadly distributed in space. On the other hand, as discussed in the next section, there is not yet conclusive evidence that even a single cluster is in a state of statistical equilibrium; if we assume that the bright and faint members of a cluster do, in fact, occupy the same volume of space, and if we can distinguish cluster from field galaxies, then we can obtain an estimate of the cluster size. There is some justification for this assumption, at least for a few irregular clusters. Dwarf elliptical galaxies in both the Virgo cluster (Reaves 1956, 1964) and the Fornax cluster (Hodge, Pyper, and Webb 1965) occupy approximately the same area in the sky as the bright cluster members (although they do not necessarily have the same spatial distribution). The angular diameter of the Virgo cluster (Sandage 1958) is about 7°; the corresponding linear diameter is about 3 × 106 pc (for H = 50 km s-1 Mpc-1). The irregular Hercules cluster (cluster 2151) has dimensions of about 3.8 × 106 by 2.5 × 106 pc (Burbidge and Burbidge 1959b). The Local Group is about 1 × 106 pc in diameter. The sizes of the rich regular clusters are more controversial (see below), but are probably of about the same order.
The sizes of the largest clusters in the Catalogue of Galaxies and Clusters of Galaxies are discussed by Zwicky and his collaborators (Zwicky and Rudnicki 1963; Zwicky and Berger 1965; Zwicky and Karpowicz 1965, 1966). Although there is considerable scatter in the data, they report that the largest clusters of all types (compact, medium compact, and open) have about the same size, which is of the order 107 pc. This is actually a lower limit for it is the diameter corresponding to Zwicky's isopleth where the surface density of galaxies is twice that of the field, and not to the entire clusters.
The irregular clusters do not display symmetry or regular structure. Multiple condensations of galaxies, however, are often present. A statistical study of the surface distribution of galaxies in seven rich clusters was made to estimate the extent of subclustering within them (Abell, Neyman, and Scott 1964). Counts of galaxies in rings centered on galaxies within the clusters are compared to counts in rings centered on arbitrary grid points. Higher mean counts in the rings surrounding galaxies than in those around the grid points (after correction for any central concentration of the cluster as a whole) indicates subclustering, and analysis of the counts gives information on the extent of the subclustering. Of the clusters investigated to date, all that are irregular show evidence of subclustering; the two most regular clusters (1656 and 2065) do not. The subgroups appear to have characteristic radii of the order 105 pc. There are, of course, two subgroups in the Local Group - centered on the Galaxy and on M31. It is also well known that double and multiple galaxies are common in certain other irregular clusters; Holmberg (1937) and van den Bergh (1960) have called attention to probable binary systems in the Virgo cluster; and the Burbidges (1959b), to such systems in the Hercules cluster.
The rich regular clusters, which show high central concentration and spherical symmetry, and little or no subclustering, are amenable to representation by theoretical models of galaxy distribution. Data on the surface distributions of galaxies in a fair number of clusters (both regular and irregular) are now published, although the completeness, quality, and format of the data vary considerably from cluster to cluster. Fortunately some clusters have been studied independently by several investigators; comparison of their results can be a valuable aid in assessing the reliability of the available material. Some references to the distribution of galaxies in clusters (listed by number in the Abell catalog) are:
| 31 | N. Bahcall (1972) |
| 234 | Zwicky (1956) |
| 426 (Perseus) | Zwicky (1957); Rudnicki (1963) |
| 732 | Zwicky (1956) |
| 801 | Zwicky (1956) |
| 1060 (Hydra I) | Zwicky (1957); Kwast (1966) |
| 1132 | N. Bahcall (1971) |
| 1185 | Rudnicki and Baranowska (1966b) |
| 1213 | Rudnicki and Baranowska (1966b) |
| 1367 | Rudnicki and Baranowska (1966a) |
| 1643 | Zwicky (1956) |
| 1656 (Coma) | Zwicky (1937, 1942b, 1957, 1959); Omer, Page, |
| and Wilson (1965); Noonan (1971); Rood | |
| et al (1972); N. Bahcall (1973b) | |
| 1677 | Zwicky (1956) |
| 2065 (Corona Borealis) | Zwicky (1956); Noonan (1971) |
| 2199 | Clark (1968); Rood and Sastry (1972); N. Bahcall (1973c) |
| Cancer | Zwicky (1957) |
| Pegasus | Zwicky (1957) |
Counts in six clusters by the writer are as yet unpublished, except for a summary of the counts in cluster 1656 by Noonan (1961a, b). The counts of galaxies on the Lick astrographic plates by Shane and his collaborators reveal many conspicuous clusters, and isopleths for several of these have been published separately by Shane (1956b).
Several types of analytical representation of the galaxy distribution in
rich clusters
have been attempted. Zwicky has fit the projected distribution of
galaxies in several
clusters to a bounded isothermal distribution projected on a plane. An
early solution for the density distribution in the isothermal polytrope
was by
Emden (1907),
who tabulates the density as a function of the dimensionless variable
 ,
representing the radial
distance from the center of the configuration. Zwicky relates the linear
distance r from the center of a cluster of galaxies to Emden's
,
representing the radial
distance from the center of the configuration. Zwicky relates the linear
distance r from the center of a cluster of galaxies to Emden's
 by
r =
by
r = 
 , and calls the
scale factor
, and calls the
scale factor  the
structural index of the cluster. The values he reports for
the
structural index of the cluster. The values he reports for
 (1957), translated to the
distance scale used in this review (H = 50 km s-1
Mpc-1), are 24.2, 25.0, 32.3, and 13.8 (in
units of 1022 cm) for clusters 1656, 1060, 426, and the Cancer
cluster, respectively.
Zwicky cites the rather small spread in the values for
(1957), translated to the
distance scale used in this review (H = 50 km s-1
Mpc-1), are 24.2, 25.0, 32.3, and 13.8 (in
units of 1022 cm) for clusters 1656, 1060, 426, and the Cancer
cluster, respectively.
Zwicky cites the rather small spread in the values for
 among
different clusters (actually,
the spread is about a factor of 2) as evidence that all regular clusters
are similar in
size and structure. The writer's counts in cluster 1656 have also been
compared with the
isothermal polytrope, both by himself (unpublished) and by
Noonan (1961a, b).
The isothermal representation is a satisfactory one, but the writer finds
among
different clusters (actually,
the spread is about a factor of 2) as evidence that all regular clusters
are similar in
size and structure. The writer's counts in cluster 1656 have also been
compared with the
isothermal polytrope, both by himself (unpublished) and by
Noonan (1961a, b).
The isothermal representation is a satisfactory one, but the writer finds
 = 48 ×
1022 cm - almost twice Zwicky's value. More recently
N. Bahcall (1972,
1973a,
c)
has shown that
the galaxy distribution in several clusters can be matched
satisfactorily to the isothermal
polytrope, and she suggests further that the structural index (or an
equivalent scaling
factor) can be used, statistically, as a distance indicator for clusters.
= 48 ×
1022 cm - almost twice Zwicky's value. More recently
N. Bahcall (1972,
1973a,
c)
has shown that
the galaxy distribution in several clusters can be matched
satisfactorily to the isothermal
polytrope, and she suggests further that the structural index (or an
equivalent scaling
factor) can be used, statistically, as a distance indicator for clusters.
In distant clusters of small angular size,
Zwicky (1956)
explains that
 is difficult to
determine with precision. For such remote systems, he introduces another
parameter, which he calls the distribution index, DI, defined by
is difficult to
determine with precision. For such remote systems, he introduces another
parameter, which he calls the distribution index, DI, defined by
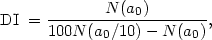
| (6) |
where N(a0) and N(a0 / 10) are the total numbers of cluster galaxies within angular distances a0 and a0/10 of the cluster center, respectively, after subtraction of na galaxies for each square degree. The quantity na is the mean number of galaxies per square degree along the circle of radius a0, and thus represents an upper limit to the density of field galaxies. Zwicky chooses a0 to be inversely proportional to the redshift of the cluster, so that it presumably corresponds to the same linear distance from the center in a nearby as in a remote cluster; for a cluster of redshift 51,700 km s-1, a0 has the value 10'.0. Zwicky attempts to adjust the exposure times of the cluster photographs so that the counts are extended through a similar magnitude range in all of them. If there were no central concentration of galaxies in a cluster, DI would be infinite. Actual values of DI for seven clusters are given in table 5, adapted from Zwicky (1956). The observed velocity of recession, cz, for each cluster is given, and also N(a0), which Zwicky points out is a lower limit to the total cluster population. Counts in clusters 1656 and 2065 were made with the 48-inch Schmidt telescope, and Zwicky states that it is difficult to adjust them to those made in the five more remote clusters on 200-inch telescope plates. Nevertheless, the small spread in the values of N(a0) and DI suggest a remarkable similarity among the regular clusters investigated.
| Cluster (Abell Number) | cz (km s-1) | N(a0) | DI |
| 234 | 51,700 | 461 | 0.115 |
| 732 | 61,000 | 451 | 0.110 |
| 801 | 57,600 | 391 | 0.129 |
| 1643 | 59,300 | 394 | 0.115 |
| 1656 | 6,850 | 467 | 0.084 |
| 1677 | 54,900 | 332 | 0.107 |
| 2065 | 22,000 | 551 | 0.103 |
| * Adapted from Zwicky 1956. | |||
Other investigators have experimented with different mathematical representations of the density distribution in clusters of galaxies. De Vaucouleurs (1960) and Shane and Wirtanen (1954) find that the surface density of galaxies in the Coma cluster (1656) follows closely a law of the form
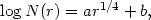
| (7) |
where N(r) is the projected density at distance r
from the center and a and b are constants.
Omer, Page, and Wilson
(1965)
have averaged counts of galaxies in parallel
strips across the same cluster by Omer, Page, and Wilson and by Shane
and have represented the counts by a series of Hermite polynomials of
even order, from which they
derived a formula for the spatial density of galaxies in the cluster.
Scott (1962)
represents Zwicky's counts in the five most distant clusters listed in
table 5 by Maxwellian distributions for which the
ratio of
 to the distance of each
cluster is 4 × 10-4; for all
five clusters, the linear value of
to the distance of each
cluster is 4 × 10-4; for all
five clusters, the linear value of
 is about
4.5 × 105 pc. All of these mathematical
distributions seem to fit actual clusters about as well as the
isothermal one. Each also
involves a fitting constant or scale factor, such as
is about
4.5 × 105 pc. All of these mathematical
distributions seem to fit actual clusters about as well as the
isothermal one. Each also
involves a fitting constant or scale factor, such as
 , DI, or
, DI, or
 ; and if, as seems
possible, the rich regular clusters are similar to one another, the
relevant scale factor might prove
valuable as a criterion for cluster distances - at least statistically.
; and if, as seems
possible, the rich regular clusters are similar to one another, the
relevant scale factor might prove
valuable as a criterion for cluster distances - at least statistically.
An observation important to the study of the dynamics of a cluster is to determine whether there is a segregation of its bright and faint galaxies. If it has reached a state of equipartition of energy, the fainter - presumably less massive - galaxies should fill a larger volume of space than the brighter ones. Zwicky (1942b) presents evidence that such a segregation exists among the brighter Virgo cluster galaxies; but there is also a segregation according to galaxy type, the spirals showing a larger radial distribution than the ellipticals. Both Holmberg (1962b) and de Vaucouleurs (1961b) have shown that the mean radial velocities are different for the spirals and ellipticals in the cluster. De Vaucouleurs argues a strong case that the Virgo cluster is really (at least) two clusters seen in projection - one being a compact cluster of elliptical and S0 galaxies, and the other a loose open cluster consisting mostly of spirals and irregulars. If de Vaucouleurs's interpretation is correct, then differences in the radial distributions of Virgo cluster galaxies of different types and/or magnitude cannot be regarded as evidence of segregation.
Rudnicki (1963), who has counted galaxies in cluster 426, believes that in that cluster the faint galaxies show a wider surface distribution than the bright ones. Unfortunately, one side of cluster 426 is partially hidden by interstellar absorption, and Rudnicki may have adopted too low an estimate for the density of galaxies that are in the field; a moderate and entirely possible increase in the field estimate completely removes the apparent segregation of bright and faint galaxies in that cluster.
Hodge, Pyper, and Webb (1965) have compared the distribution of the 50 faint galaxies they discovered in the Fornax cluster to that of the brighter cluster members. They find that cluster membership is too difficult to ascertain farther than 4° from the center, so they limit their comparison to the inner regions. There, the faint galaxies appear to show less central concentration, suggesting that a real Segregation exists. Unfortunately, the number of bright galaxies is small (about 20), and small sample fluctuations or subclustering may influence the picture.
The fact that the peak at the bright end of the luminosity function of the Coma cluster seems to be at least partially due to brighter galaxies at the cluster center (Rood 1969; Rood and Abell 1973) indicates some dependence of the galaxy distribution in the cluster on galaxian mass. N. Bahcall (1972, 1973c) finds some possible segregation by mass of galaxies in cluster A31, but no evidence for the same in cluster 2199. Kwast (1966) finds the bright and intermediate galaxies in A1060 to have the same distribution, but the faint galaxies in the cluster to be more broadly distributed. Rudnicki and Baranowska (1966a, b) find some evidence for mass segregation in A1185 and A1213, but not in A1367.
The best studied cluster, and the best example for discussion, is the Coma cluster (1656). Here again, different investigators disagree on the size of the cluster and the distribution of bright and faint galaxies. Zwicky (1957) holds that the cluster is at least 6° in radius, that it contains about 104 members brighter than mpg = 19, and that there is marked segregation of its brighter and fainter members. Noonan (1961a, b), however, has reanalyzed Zwicky's own published counts and finds the cluster to be only 100' in radius, and to have identical distributions of bright and faint galaxies. Omer, Page, and Wilson (1965), from the analysis of their own and of Shane's counts in the Coma cluster, arrive at the same conclusion as Noonan. These different conclusions result from different interpretations of the surface density of field galaxies. The mean field density is quite constant from 2° to 6° from the cluster center, but is slightly lower in some directions at a distance just beyond 6°. Zwicky interprets the lower average density 6° to 7° from the cluster as the true field and attributes the excess of faint galaxies at distances less than 6° to cluster membership. The other investigators interpret the higher density from 2° to 6° as the correct field, in which case there is not an excess of faint galaxies with a larger radial distribution than the bright ones; the total cluster population to mpg ~ 19 is then only about 103.
The writer (Abell 1963)
finds the cluster to be slightly elongated in a
northeast-southwest direction, and to be probably contained within an
oval region of dimensions
5.4° × 4.3°. The oval shape of the cluster is also
apparent in the equal-density contours of
Shane and Wirtanen (1954),
and in unpublished data of Reaves
(Omer, Page, and Wilson
1965).
To the magnitude limit
mpv = 18.3, he has found that in a 70
square-degree area outside this oval region the number of galaxies
brighter than magnitude m is given by
log N(mpv) = constant +
0.6mpv, which is expected if these are field galaxies
distributed at random through space. At most, only a few percent of
these galaxies can
be faint outlying cluster members. Thus, the cluster cannot contribute
appreciably to the field beyond the
5.4° × 4.3° region. The writer
adopts 77 galaxies per square degree (with
mpv  18.3)
as a lower limit to this field density; the
correct value may be a little
higher, because the average is taken over an area which includes the
low-density region
several degrees away from the cluster center. If the counts within the
oval cluster region
are corrected for this field density, the luminosity function obtained
for the cluster is the
one given in table 2. The radial
spatial distributions of galaxies
brighter than mpv = 16.0 and in the range
mpv = 16.0 - 18.3, derived from averaged counts
in north-south and
east-west strips across the cluster, are shown in
figure 6. The slight segregation of the
brighter and fainter galaxies that appears to be exhibited in
figure 6
may result from the
adoption of slightly too low a field density; this, in other words, is
an upper limit to the
segregation of bright and faint galaxies. The writer's results are not
incompatible with
those of Noonan and of Omer, Page, and Wilson, who find no segregation
at all, and a total cluster radius of 100', or
4 × 106 pc. In
addition, they are compatible with results of
N. Bahcall (1973b),
who finds no evidence for segregation of bright and faint galaxies
except possibly for a slightly (20 percent) higher concentration of the
brightest cluster galaxies near the core.
18.3)
as a lower limit to this field density; the
correct value may be a little
higher, because the average is taken over an area which includes the
low-density region
several degrees away from the cluster center. If the counts within the
oval cluster region
are corrected for this field density, the luminosity function obtained
for the cluster is the
one given in table 2. The radial
spatial distributions of galaxies
brighter than mpv = 16.0 and in the range
mpv = 16.0 - 18.3, derived from averaged counts
in north-south and
east-west strips across the cluster, are shown in
figure 6. The slight segregation of the
brighter and fainter galaxies that appears to be exhibited in
figure 6
may result from the
adoption of slightly too low a field density; this, in other words, is
an upper limit to the
segregation of bright and faint galaxies. The writer's results are not
incompatible with
those of Noonan and of Omer, Page, and Wilson, who find no segregation
at all, and a total cluster radius of 100', or
4 × 106 pc. In
addition, they are compatible with results of
N. Bahcall (1973b),
who finds no evidence for segregation of bright and faint galaxies
except possibly for a slightly (20 percent) higher concentration of the
brightest cluster galaxies near the core.
Rood et al. (1972) also concur that there is no marked segregation of bright and faint galaxies in the Coma cluster. However, they find the cluster to have a radius of 200'. The writer thinks it possible that the larger size Rood et al. find may result from their treating as members some outlying galaxies that may be part of a superstructure of galaxies that do not really belong to the main Coma cluster concentration. However, this question bears on how a cluster is defined in the first place, and there exists no unambiguous agreed-on operational definition. As remarked earlier, answers to such questions as the memberships, sizes, and distributions of galaxies of different masses within clusters depend on how clusters are defined and how their members are distinguished from the field. Differences between how these matters are handled may well account for the diversification of results described in this section.