The existence of multiple thermal phases is made possible by the flow of
energy into and out
of a system. Multiple phases do not develop in systems which are
thermodynamically isolated
from their surroundings. If
(n, T,
xj) is the heating rate per particle and
(n,
T, xj)
is the cooling function, then the equation of thermal equilibrium may be
written
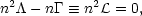
| (1) |
where n is the density of hydrogen nuclei, T is the
temperature, and xj represents the
fractional concentrations of various species,
xj 
nj/n. The pressure is given by
p = xtnkT, where xt =
xj is the
number of particles per hydrogen nucleus. An equation analogous
to (1) determines the ionization equilibrium.
, and sometimes
(e.g., in the
case of inverse Compton cooling), may also depend on the magnitude of some
external heating or ionization agent, which has energy density
u. If
u
is held fixed then the solution of the
equilibrium equations generates a curve in the
p - n, p - V (where
V 1/n is
the specific
density) or p - T plane which separates the heating region
( >
n) from the
cooling region ( <
n). In
general these curves may have complex shapes and be multivalued.
If there are two or more values of n (or, equivalently, of T), which correspond to a given pressure, then a multiphase equilibrium is possible: a relatively cool, dense region can coexist with one or more warmer, less dense regions in pressure equilibrium. If this configuration is thermally stable (see Section 2.2 below), and if there is no mass exchange between phases, then this equilibrium can persist indefinitely. Simple generic examples of multiphase equilibria are shown in Figure 1. In all cases we have assumed that there is a single stable "cloud" phase with a fixed temperature Tcl. Figs. 1 b and 1 d both show systems with two stable phases, while the other panels show systems with only one stable phase. More realistic phase diagrams may show three or more stable phases, e.g., Lepp et al. (1985).
|
Figure 1. Radiative thermal equilibrium in the p - V plane. Cooling exceeds heating above the solid line. Clouds exist for pressures exceeding pmin their temperature is fixed at Tcl. a) One thermally stable phase. b) Two thermally stable phases separated by a thermally unstable phase. c) Thermally stable clouds in a thermally unstable intercloud medium. d) If p(V) is multivalued (corresponding to gas at a given density having one of several temperatures), the gas may be isochorically as well as isobarically unstable. |
In most cases of astrophysical interest,
is linear in
u.
If both and
are
independent of density (as in particle or photon heating and two-body
cooling) or depend on density through the ratio n /
u
(as in the case of inverse Compton cooling), then both the
ionization level and the temperature depend on n and
u only
through the combination n /
u
or, equivalently, p /
u.
This similarity
variable is very useful for characterizing the
state of gas heated by cosmic rays
(Dalgarno and McCray 1972)
or radiation (e.g.,
Tarter, Tucker and Salpeter
1969;
Davidson 1972;
Krolik, McKee and Tarter
1981);
in various forms it is referred to as the ionization parameter.
Not all thermal phases which are observed in astrophysical systems correspond to stable equilibria. Examples of systems which exhibit long-lived non-equilibrium hot phases, in pressure balance with a stable cold phase, are the three-phase interstellar medium (McKee and Ostriker 1977) and cooling flows in clusters of galaxies (Sarazin 1986, and references therein). The non-equilibrium phases in these systems are in fact thermally unstable, and are observable only because their cooling time scales are extremely long (Spitzer 1956). An accurate analysis of such systems requires the treatment of time-dependence (McKee and Ostriker 1977) and hydrodynamical effects such as buoyancy (Balbus and Soker 1989).